���嗝�n���w'02�N�O��[6]
N�𐳂̐����Ƃ���B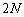 �̍�����Ȃ鐔��
�̍�����Ȃ鐔��
��
�Ƃ�������ɕ��בւ��鑀����u�V���b�t���v�ƌĂԂ��Ƃɂ���B���בւ��������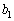 �������Ƃ��A
�������Ƃ��A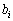 �̎���
�̎���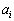 �C
�C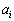 �̎���
�̎���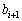 ������悤�Ȃ��̂ɂȂ�B�܂��A����
������悤�Ȃ��̂ɂȂ�B�܂��A����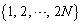 ���V���b�t�������Ƃ��ɓ����鐔��ɂ����āA��k�������ʒu��
���V���b�t�������Ƃ��ɓ����鐔��ɂ����āA��k�������ʒu��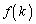 �ŕ\���B
�ŕ\���B
���Ƃ��A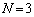 �̂Ƃ��A
�̂Ƃ��A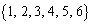 ���V���b�t�������
���V���b�t�������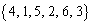 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA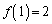 �C
�C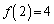 �C
�C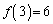 �C
�C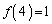 �C
�C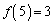 �C
�C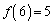 �ł���B
�ł���B
(1) ����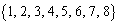 ��3��V���b�t�������Ƃ��ɓ����鐔������߂�B
��3��V���b�t�������Ƃ��ɓ����鐔������߂�B (2) 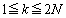 �����C�ӂ̐���k�ɑ��A
�����C�ӂ̐���k�ɑ��A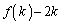 ��
��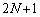 �Ŋ����邱�Ƃ������B
�Ŋ����邱�Ƃ������B (3) n�𐳂̐����Ƃ��A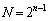 �̂Ƃ����l����B����
�̂Ƃ����l����B����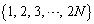 ��
��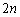 ��V���b�t������ƁA
��V���b�t������ƁA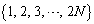 �ɂ��ǂ邱�Ƃ��ؖ�����B
�ɂ��ǂ邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2002�N�O���̓���̖��́A���̖�肪�l���ɂ����̂ŁA�����Ղ��������̂����m��܂���B
(1) �e�ƂɃV���b�t���������ʂ������Ă݂܂��B
(2) ��蕶�̂܂܍l���悤�Ƃ��Ă��A��قǂ̓V�˂łȂ�����A���������Ȃ��Ǝv���܂��B
�����Ŗ�肪������Ă���̂Œ��ۓI�ŁA�ǂ̂悤�Ȃ��Ƃ������Ă�����Ȃ̂��A���������߂Ȃ��̂ł��B
�����������́A��̓I�ɐ��l�������āA���ׂĂ����܂��B(1)�ł�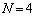 �̏ꍇ�ׂ܂����B�����ł�
�̏ꍇ�ׂ܂����B�����ł�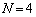 �Ƃ��čl���Ă݂܂��B1��V���b�t����������
�Ƃ��čl���Ă݂܂��B1��V���b�t����������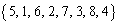 �ɂ��āA8��ނ̐��̊e�X�ɂ��āA
�ɂ��āA8��ނ̐��̊e�X�ɂ��āA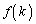 ��
��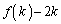 (
(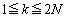 )�̓����ׂĂ݂܂��B���\�ŁA�Ⴆ�A�ォ��6�s�ڂɁA 6, 3,
)�̓����ׂĂ݂܂��B���\�ŁA�Ⴆ�A�ォ��6�s�ڂɁA 6, 3, 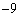 �Ɛ�������ł��܂����A����́A(1)��1��V���b�t���������ʁA6��3�Ԗڂɏo�Ă��āA
�Ɛ�������ł��܂����A����́A(1)��1��V���b�t���������ʁA6��3�Ԗڂɏo�Ă��āA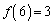 �C
�C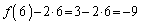 �ł��邱�Ƃ��Ӗ����Ă��܂��B
�ł��邱�Ƃ��Ӗ����Ă��܂��B
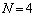 �̂Ƃ��A
�̂Ƃ��A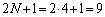 �ł����A
�ł����A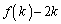 �̗��ɕ���ł��鐔�́A0��
�̗��ɕ���ł��鐔�́A0��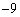 �Ȃ̂ŁA
�Ȃ̂ŁA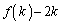 ��9�Ŋ����܂��B
��9�Ŋ����܂��B
������A��ʓI�Ȑ��̐���N�ɂ��Ď����A�ƁA�����Ă���̂ł��B
�܂��A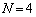 �̏ꍇ���ɂƂ�Ȃ���A���j�𗧂Ă܂��B�\������ƁA2�̃^�C�v�ɕ�����邱�Ƃɂ����C�Â��܂��B
�̏ꍇ���ɂƂ�Ȃ���A���j�𗧂Ă܂��B�\������ƁA2�̃^�C�v�ɕ�����邱�Ƃɂ����C�Â��܂��B
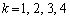 �̃O���[�v(���4�s)��
�̃O���[�v(���4�s)��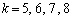 �̃O���[�v(����4�s)�ł��B1��V���b�t���������ʂ߂�ƁA
�̃O���[�v(����4�s)�ł��B1��V���b�t���������ʂ߂�ƁA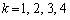 �̃O���[�v�ł́A
�̃O���[�v�ł́A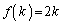 �ɂȂ��Ă��邱�Ƃ��킩��܂��B
�ɂȂ��Ă��邱�Ƃ��킩��܂��B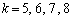 ��1���݂��Ⴂ�Ɋ��荞��ł��邩��ł��B
��1���݂��Ⴂ�Ɋ��荞��ł��邩��ł��B
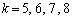 �̃O���[�v�ł́A
�̃O���[�v�ł́A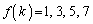 �ɂȂ��Ă��܂����A����͂ǂ̂悤�Ȏd�|���ɂȂ��Ă���̂ł��傤���H1��V���b�t����������
�ɂȂ��Ă��܂����A����͂ǂ̂悤�Ȏd�|���ɂȂ��Ă���̂ł��傤���H1��V���b�t����������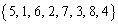 ������ƁA���̃O���[�v�̐擪��5��1�Ԗڂɓ���A�Ȍ�A2�̃O���[�v���݂��Ⴂ�ɓ���̂ŁA1������6, 7, 8������A6��3�ԖځA7��5�ԖځA8��7�ԖڂƂ�����ɓ����Ă����܂��B
������ƁA���̃O���[�v�̐擪��5��1�Ԗڂɓ���A�Ȍ�A2�̃O���[�v���݂��Ⴂ�ɓ���̂ŁA1������6, 7, 8������A6��3�ԖځA7��5�ԖځA8��7�ԖڂƂ�����ɓ����Ă����܂��B
��ʓI�ɁA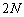 �̍�����Ȃ鐔��
�̍�����Ȃ鐔��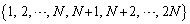 ��O����N�̃O���[�v
��O����N�̃O���[�v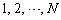 �ƌ㔼��N�̃O���[�v
�ƌ㔼��N�̃O���[�v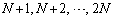 �ɕ����܂��B
�ɕ����܂��B
�V���b�t������ƁA�擪��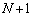 �ɂȂ�܂��B
�ɂȂ�܂��B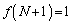 �ł��B2�Ԗڂ́A1�ɂȂ�܂��B
�ł��B2�Ԗڂ́A1�ɂȂ�܂��B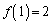 �ł��B
�ł��B
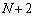 ���珇��
���珇�� �܂ŁA1�Ԗڂ�
�܂ŁA1�Ԗڂ�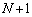 ���A1�����ɁA3�ԖځA5�ԖځA����Ƃ�����ɓ����Ă����̂ŁA
���A1�����ɁA3�ԖځA5�ԖځA����Ƃ�����ɓ����Ă����̂ŁA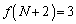 �C
�C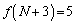 �C����C
�C����C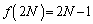
�����A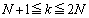 �ƂȂ鐮��k�ɂ��āA
�ƂȂ鐮��k�ɂ��āA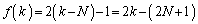 �ƂȂ�܂�(
�ƂȂ�܂�(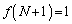 �C
�C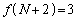 �Ȃǂ��m���߂Ă�������)�B2���珇��N�܂ŁA1�̓�����2�Ԗڂ̈ʒu���A1�����ɁA4�ԖځA6�ԖځA����Ƃ�����ɓ����Ă����̂ŁA
�Ȃǂ��m���߂Ă�������)�B2���珇��N�܂ŁA1�̓�����2�Ԗڂ̈ʒu���A1�����ɁA4�ԖځA6�ԖځA����Ƃ�����ɓ����Ă����̂ŁA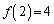 �C
�C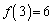 �C����C
�C����C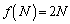
�����A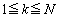 �ƂȂ鐮��k�ɂ��āA
�ƂȂ鐮��k�ɂ��āA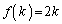 �ƂȂ�܂��B
�ƂȂ�܂��B
�ȏ���A
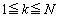 �ƂȂ鐮��k�ɂ��āA
�ƂȂ鐮��k�ɂ��āA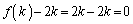 ��
��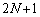 �Ŋ����܂��B
�Ŋ����܂��B
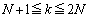 �ƂȂ鐮��k�ɂ��āA
�ƂȂ鐮��k�ɂ��āA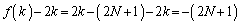 ��
��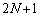 �Ŋ����܂��B
�Ŋ����܂��B
����āA������܂����B
(3) (1)���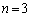 �̂Ƃ��A�܂�
�̂Ƃ��A�܂�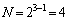 �̂Ƃ��An��A�܂�3��V���b�t������ƁA���傤�Ǐ��Ԃ������ɂȂ邱�Ƃ��킩��܂��B�]���āA�����n��v
�̂Ƃ��An��A�܂�3��V���b�t������ƁA���傤�Ǐ��Ԃ������ɂȂ邱�Ƃ��킩��܂��B�]���āA�����n��v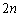 ��A�܂�A�͂��߂���6��V���b�t������A���Ԃ��܂������ɂȂ��āA���ɖ߂�킯�ł��B
��A�܂�A�͂��߂���6��V���b�t������A���Ԃ��܂������ɂȂ��āA���ɖ߂�킯�ł��B m��(m�́A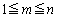 ��������)�V���b�t�������Ƃ���k�̈ʒu��
��������)�V���b�t�������Ƃ���k�̈ʒu��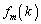 �Ə������Ƃɂ��܂��B
�Ə������Ƃɂ��܂��B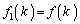 �ł��B
�ł��B
�����ׂ����ƁA�܂�A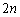 ��V���b�t�����ď��Ԃ����ɖ߂�Ƃ������Ƃ́A
��V���b�t�����ď��Ԃ����ɖ߂�Ƃ������Ƃ́A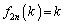 �ƂȂ�A�Ƃ������Ƃł��B(1)��
�ƂȂ�A�Ƃ������Ƃł��B(1)��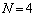 �̏ꍇ�ׂ܂������A����𗘗p���āA
�̏ꍇ�ׂ܂������A����𗘗p���āA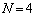 �̏ꍇ�ɂ��āA�V���b�t�����邲�Ƃ�k���ǂ��Ɉړ����邩�A
�̏ꍇ�ɂ��āA�V���b�t�����邲�Ƃ�k���ǂ��Ɉړ����邩�A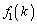 �C
�C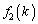 �C
�C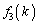 �ׂĂ݂܂��B
�ׂĂ݂܂��B| k | 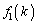 | 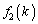 | 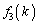 |
| 1 | 2 | 4 | 8 |
| 2 | 4 | 8 | 7 |
| 3 | 6 | 3 | 6 |
| 4 | 8 | 7 | 5 |
| 5 | 1 | 2 | 4 |
| 6 | 3 | 6 | 3 |
| 7 | 5 | 1 | 2 |
| 8 | 7 | 5 | 1 |
���\�ŁA�Ⴆ�A�ォ��4�s�ڂ�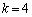 �̂Ƃ���́A8, 7, 5�ƂȂ��Ă��܂����A
�̂Ƃ���́A8, 7, 5�ƂȂ��Ă��܂����A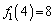 �C
�C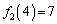 �C
�C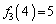 �C�܂�A4�́A1��V���b�t�������8�ԖڂɁA2��V���b�t�������7�ԖڂɁA3��V���b�t�������5�Ԗڂɗ���A�Ƃ����Ӗ��ł��B
�C�܂�A4�́A1��V���b�t�������8�ԖڂɁA2��V���b�t�������7�ԖڂɁA3��V���b�t�������5�Ԗڂɗ���A�Ƃ����Ӗ��ł��B
�����ŁA��C�����������Ƃ�����܂��B(2)��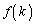 ����
����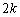 ���������Ƃ�
���������Ƃ�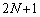 �Ŋ����邱�Ƃ��m���߂܂����B��������p���Ă݂܂��B(2)�ł́A
�Ŋ����邱�Ƃ��m���߂܂����B��������p���Ă݂܂��B(2)�ł́A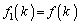 �����
�����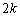 ��������9�Ŋ����邱�Ƃ��m���߂��̂ł����A
��������9�Ŋ����邱�Ƃ��m���߂��̂ł����A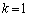 �ɑ��āA�V���b�t�����邲�ƂɁA
�ɑ��āA�V���b�t�����邲�ƂɁA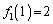 �C
�C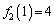 �C
�C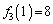 �ƁA2�{������čs���܂��B
�ƁA2�{������čs���܂��B
�����ŁA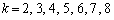 �ɂ��Ă��A�V���b�t�����邲�Ƃ�2�{�����čs���A
�ɂ��Ă��A�V���b�t�����邲�Ƃ�2�{�����čs���A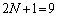 �Ŋ��������̂��l���܂��B
�Ŋ��������̂��l���܂��B
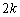 ��9�Ŋ���ƁA
��9�Ŋ���ƁA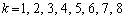 �ɑ��āA9�Ŋ������]��́A
�ɑ��āA9�Ŋ������]��́A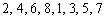 �ƂȂ�A
�ƂȂ�A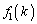 �ƈ�v���܂��B
�ƈ�v���܂��B
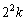 ��9�Ŋ���ƁA
��9�Ŋ���ƁA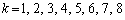 �ɑ��āA9�Ŋ������]��́A
�ɑ��āA9�Ŋ������]��́A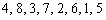 �ƂȂ�A
�ƂȂ�A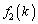 �ƈ�v���܂��B
�ƈ�v���܂��B
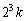 ��9�Ŋ���ƁA
��9�Ŋ���ƁA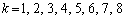 �ɑ��āA9�Ŋ������]��́A
�ɑ��āA9�Ŋ������]��́A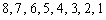 �ƂȂ�A
�ƂȂ�A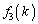 �ƈ�v���܂��B
�ƈ�v���܂��B
�����ŁA��ʓI�ɁA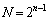 �̂Ƃ��Am�����R���Ak��
�̂Ƃ��Am�����R���Ak��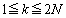 �����������Ƃ��āA
�����������Ƃ��āA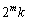 ��
��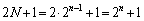 �Ŋ������]�肪
�Ŋ������]�肪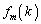 �ƈ�v���邱�ƁA�܂�A����
�ƈ�v���邱�ƁA�܂�A����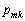 �Ƃ��āA
�Ƃ��āA 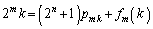 �@����@
�@����@
(�T) 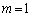 �̂Ƃ��A(2)���A
�̂Ƃ��A(2)���A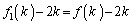 �́A
�́A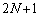 �Ŋ�����̂ŁA����
�Ŋ�����̂ŁA����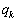 �Ƃ��āA
�Ƃ��āA �� 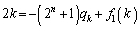 ����A
����A
����́A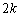 ��
��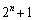 �Ŋ���ƁA�]�肪
�Ŋ���ƁA�]�肪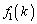 �ł��邱�Ƃ��Ӗ����܂��B
�ł��邱�Ƃ��Ӗ����܂��B
(�U) 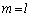 �̂Ƃ����藧�Ƃ��܂��B
�̂Ƃ����藧�Ƃ��܂��B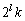 ��
��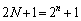 �Ŋ������]�肪
�Ŋ������]�肪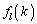 �ƈ�v����̂ŁA
�ƈ�v����̂ŁA ���ӂ�2�������āA
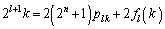 ����B
����B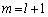 �̏ꍇ���l����̂ɓ������āA���̎��ɏo�Ă���
�̏ꍇ���l����̂ɓ������āA���̎��ɏo�Ă���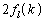 �����Ƃ����Ȃ��Ă͂����܂���B
�����Ƃ����Ȃ��Ă͂����܂���B
���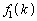 �C
�C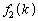 �C
�C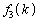 �̕\���悭����ƁA�ǂ̗��ɂ����Ă��A1�̎��ɂ�2�C2�̎��ɂ�4�C3�̎��ɂ�6�C4�̎��ɂ�8�C5�̎��ɂ�1�C6�̎��ɂ�3�C7�̎��ɂ�5�C8�̎��ɂ�7�����܂��B�Ƃ������Ƃ́A
�̕\���悭����ƁA�ǂ̗��ɂ����Ă��A1�̎��ɂ�2�C2�̎��ɂ�4�C3�̎��ɂ�6�C4�̎��ɂ�8�C5�̎��ɂ�1�C6�̎��ɂ�3�C7�̎��ɂ�5�C8�̎��ɂ�7�����܂��B�Ƃ������Ƃ́A �́A
�́A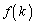 ��k��
��k��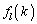 �Ƃ������̂Ɉ�v����(
�Ƃ������̂Ɉ�v����(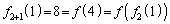 �C
�C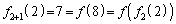 �C
�C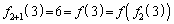 �C���)�A�Ƃ������Ƃł��B�܂�A
�C���)�A�Ƃ������Ƃł��B�܂�A����������ƁAk��l��V���b�t������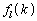 �Ԗڂ̈ʒu�ɂ����Ƃ��āA���̃V���b�t���łǂ��ɍs����(���ꂪ�A
�Ԗڂ̈ʒu�ɂ����Ƃ��āA���̃V���b�t���łǂ��ɍs����(���ꂪ�A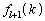 �ł�)�ƌ����ƁA�ŏ���
�ł�)�ƌ����ƁA�ŏ���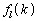 �Ԗڂ̈ʒu�ɂ����̂�k�Ȃ̂ŁAk��1��V���b�t�����čs���ʒu
�Ԗڂ̈ʒu�ɂ����̂�k�Ȃ̂ŁAk��1��V���b�t�����čs���ʒu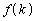 �Ɠ����ʒu�ɍs���A�܂�A
�Ɠ����ʒu�ɍs���A�܂�A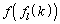 �ɍs���A�Ƃ������Ƃł��B
�ɍs���A�Ƃ������Ƃł��B
�A��k��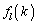 �ɓ���ւ���ƁA
�ɓ���ւ���ƁA ������B�ɑ������ƁA
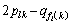 �͐����Ȃ̂ŁA����́A
�͐����Ȃ̂ŁA����́A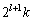 ��
��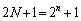 �Ŋ������]�肪
�Ŋ������]�肪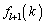 �ł��邱�Ƃ��Ӗ����܂��B�܂�A
�ł��邱�Ƃ��Ӗ����܂��B�܂�A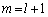 �ɂ����Ă����藧���܂��B
�ɂ����Ă����藧���܂��B(�T)�C(�U)���A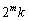 ��
��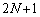 �Ŋ������]��́A
�Ŋ������]��́A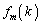 �ƈ�v���܂��B
�ƈ�v���܂��B
�����ŁA�@�ɂ����āA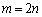 �Ƃ���ƁA
�Ƃ���ƁA �� 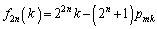
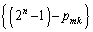 �͐����Ȃ̂ŁA����́A
�͐����Ȃ̂ŁA����́A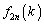 ��
��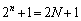 �Ŋ������]�肪k�ł��邱�Ƃ��Ӗ����Ă��܂��B
�Ŋ������]�肪k�ł��邱�Ƃ��Ӗ����Ă��܂��B
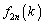 ��
��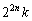 ��
��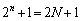 �Ŋ������]��Ȃ̂ŁA
�Ŋ������]��Ȃ̂ŁA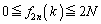
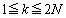 �ł�����A
�ł�����A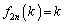 �ł��B
�ł��B
����́A����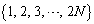 ��
��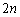 ��V���b�t������ƁA
��V���b�t������ƁA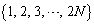 �ɂ��ǂ邱�Ƃ��Ӗ����܂��B
�ɂ��ǂ邱�Ƃ��Ӗ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B