東京大学理系2002年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 2つの放物線
が相異なる2点で交わるような一般角θ の範囲を求めよ。
[解答へ]
[2] nは正の整数とする。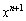
を
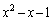で割った余りを
とおく。
を満たすことを示せ。
(2) 
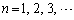に対して、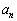
，
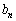は共に正の整数で、互いに素であることを証明せよ。 [解答へ]
[3] xyz空間内の原点O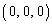
を中心とし、点A
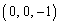を通る球面をSとする。Sの外側にある点P
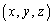に対し、OPを直径とする球面とSとの交わりとして得られる円を含む平面をLとする。点Pと点Aから平面Lへ下した垂線の足をそれぞれQ，Rとする。このとき、
であるような点Pの動く範囲Vを求め、Vの体積は10より小さいことを示せ。
[解答へ]
[4] aは正の実数とする。xy平面のy軸上に点P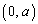
をとる。関数
のグラフをCとする。C上の点Qで次の条件を満たすものが原点O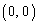
以外に存在するようなaの範囲を求めよ。
条件：QにおけるCの接線が直線PQと直交する。
[解答へ]
[5] Oを原点とするxyz空間に点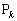
，
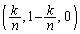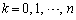，をとる。また、z軸上
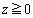の部分に、点
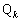を線分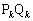
の長さが1になるようにとる。三角錐
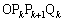の体積を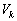
とおいて、極限
を求めよ。
[解答へ]
[6] Nを正の整数とする。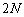
個の項からなる数列
を
という数列に並べ替える操作を「シャッフル」と呼ぶことにする。並べ替えた数列は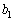
を初項とし、
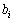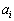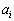の次に
，
の次に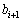
が来るようなものになる。また、数列
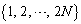をシャッフルしたときに得られる数列において、数kが現れる位置を
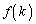で表す。
たとえば、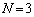
のとき、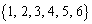
をシャッフルすると
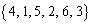となるので、
，
，
，
，
，
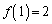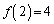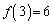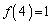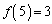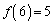である。
(1) 数列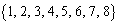
を3回シャッフルしたときに得られる数列を求めよ。 (2) 
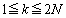を満たす任意の整数kに対し、
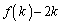は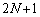
で割り切れることを示せ。 (3) nを正の整数とし、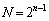
のときを考える。数列
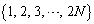を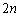
回シャッフルすると、
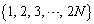にもどることを証明せよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
は
