���嗝�n���w'02�N�O��[3]
xyz��ԓ��̌��_O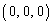 �𒆐S�Ƃ��A�_A
�𒆐S�Ƃ��A�_A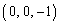 ��ʂ鋅�ʂ�S�Ƃ���BS�̊O���ɂ���_P
��ʂ鋅�ʂ�S�Ƃ���BS�̊O���ɂ���_P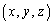 �ɑ��AOP�a�Ƃ��鋅�ʂ�S�Ƃ̌����Ƃ��ē�����~���܂ޕ��ʂ�L�Ƃ���B�_P�Ɠ_A���畽��L�։����������̑������ꂼ��Q�CR�Ƃ���B���̂Ƃ��A
�ɑ��AOP�a�Ƃ��鋅�ʂ�S�Ƃ̌����Ƃ��ē�����~���܂ޕ��ʂ�L�Ƃ���B�_P�Ɠ_A���畽��L�։����������̑������ꂼ��Q�CR�Ƃ���B���̂Ƃ��A
�ł���悤�ȓ_P�̓����͈�V�����߁AV�̑̐ς�10��菬�������Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̏ݒ��z���̂܂��ɉ�]���Ă��ω�������܂���B�]���āAP��y���W��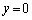 �Ƃ��Azx���ʏ�ōl���Ă����āA���Ƃ���z���̂܂��ɉ�]�����ċ�Ԑ}�`�Ƃ��čl����A�Ƃ����悤�ɂ��ł��܂��B�����ł́A��Ԑ}�`�̂܂܁A����Ă݂܂��B�Ȃ��A���L�̕⒍���Q�Ƃ��Ă��������B
�Ƃ��Azx���ʏ�ōl���Ă����āA���Ƃ���z���̂܂��ɉ�]�����ċ�Ԑ}�`�Ƃ��čl����A�Ƃ����悤�ɂ��ł��܂��B�����ł́A��Ԑ}�`�̂܂܁A����Ă݂܂��B�Ȃ��A���L�̕⒍���Q�Ƃ��Ă��������B
2�̋����o�Ă��܂����A���ꂼ��̋��ʏ�̓_�̍��W��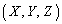 �ƕ\�����Ƃɂ��܂��B
�ƕ\�����Ƃɂ��܂��B
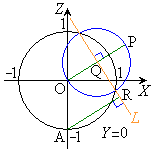 ����S�̕������́A
����S�̕������́A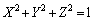 ����@�@(���ʂ̕��������Q��)
����@�@(���ʂ̕��������Q��)
OP�a�Ƃ��鋅�̒��S��T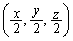 �ɂ���܂��B���̔��a��OT�ł��B
�ɂ���܂��B���̔��a��OT�ł��B
OP�a�Ƃ��鋅�ʂ̕������́A
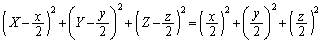 ����A
����A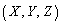 �Ƃ��āA����L�̕������́A
�Ƃ��āA����L�̕������́A
�������āA
�_P��L�Ƃ̋�����PQ�ł��B
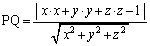 �@(���L(��)���Q��)
�@(���L(��)���Q��)
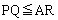 ���A
���A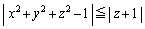 ����C
����C
�E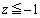 �̂Ƃ��A�C ��
�̂Ƃ��A�C �� 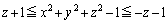
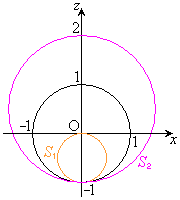 �D�̕\���}�`�́A
�D�̕\���}�`�́A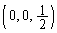 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a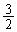 �̋���
�̋��� ����O���ł����Ă��A
����O���ł����Ă��A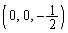 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a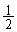 �̋���
�̋���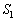 ��������̕����ł��B
��������̕����ł��B
�_P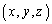 �́A����S�̊O���̓_�Ȃ̂ŁA
�́A����S�̊O���̓_�Ȃ̂ŁA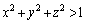 ����E
����E
�D���E�����_�͂���܂���B
�E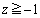 �̂Ƃ��A�C ��
�̂Ƃ��A�C �� 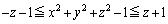
 �F�̕\���}�`�́A
�F�̕\���}�`�́A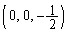 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a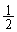 �̋���
�̋���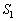 ����O���ł����Ă��A
����O���ł����Ă��A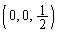 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a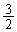 �̋���
�̋���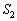 ��������̕����ł��B
��������̕����ł��B
�_P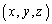 �́A����S�̊O���̓_�Ȃ̂ŁA
�́A����S�̊O���̓_�Ȃ̂ŁA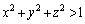 ����G
����G
�����܂��B�F���G�����_�͉E�}���ΐF���F�����ɂ���܂�(���}��������)�B
����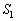 �́A����S�Ɠ_A
�́A����S�Ɠ_A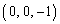 �Őڂ��A���ڂ��܂��B����
�Őڂ��A���ڂ��܂��B���� �́A����S�Ɠ_A
�́A����S�Ɠ_A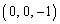 �Őڂ��A�O�ڂ��܂��B
�Őڂ��A�O�ڂ��܂��B
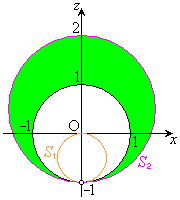
�]���āA�F���G�ɂ��A�_P�̓����͈�V�́A
���_�𒆐S�Ƃ��锼�a1�̋��ʂ��O���ł����Ă��A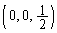 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a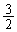 �̋���
�̋���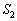 ��������ł�����
��������ł�����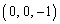 ���������� ......[��]
���������� ......[��]
V�̑̐ς́A���a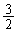 �̋��̑̐ς���A���a1�̋��̑̐ς����������̂ɂȂ�܂��B
�̋��̑̐ς���A���a1�̋��̑̐ς����������̂ɂȂ�܂��B
V�̑̐ρF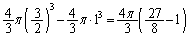
�⒍�@��L�ł́A���ʂ̕������A���ʂ̕������A�_�ƕ��ʂ̋����̌�����p���Ă��܂��B
�_C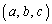 �𒆐S�Ƃ��锼�ar�̋��ʏ�̓_P
�𒆐S�Ƃ��锼�ar�̋��ʏ�̓_P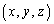 �́A
�́A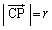 �����܂��B
�����܂��B
���W��p���ď����ƁA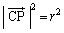 ���A
���A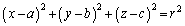
���ꂪ�A�_C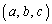 �𒆐S�Ƃ��锼�ar�̋��ʂ̕������ł��B
�𒆐S�Ƃ��锼�ar�̋��ʂ̕������ł��B
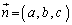 �Ɛ����ŁA�_D��ʂ镽�ʏ�̓_P
�Ɛ����ŁA�_D��ʂ镽�ʏ�̓_P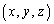 �́A
�́A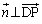 �C�����A
�C�����A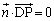 �����܂��B
�����܂��B
�� 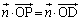
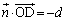 �Ƃ��āA
�Ƃ��āA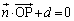 �����W��p���ď����ƁA
�����W��p���ď����ƁA
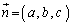 �Ɛ����ȕ��ʂ̕������́A
�Ɛ����ȕ��ʂ̕������́A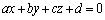 �ƕ\�����Ƃ��ł��܂��B
�ƕ\�����Ƃ��ł��܂��B
�_A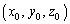 �ƕ��ʁF
�ƕ��ʁF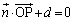 �Ƃ̋���h�́A�_A���畽�ʂɉ��낵�������̑���H�Ƃ��āA
�Ƃ̋���h�́A�_A���畽�ʂɉ��낵�������̑���H�Ƃ��āA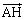 //
// 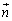 ���A
���A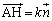 �ƕ\����̂ŁA
�ƕ\����̂ŁA
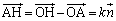 ���A
���A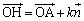
H�͕��ʏ�̓_�Ȃ̂ŁA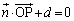 ��P��H�ɑウ���������藧���܂��B
��P��H�ɑウ���������藧���܂��B
�� 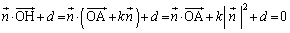
�� 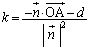
������A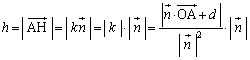
�� 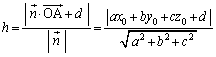 �@���(��)
�@���(��)
���ꂪ�A�_A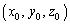 �ƕ��ʁF
�ƕ��ʁF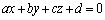 �Ƃ̋����̌����ł��B��L�̓��嗝�n���w'02�O��[3]�ł́APQ��AR�����߂�̂Ɏg���Ă��܂��B
�Ƃ̋����̌����ł��B��L�̓��嗝�n���w'02�O��[3]�ł́APQ��AR�����߂�̂Ɏg���Ă��܂��B
�܂��A��L�ł́A�@�|�A�Ƃ��āA2���̌��~���܂ޕ��ʂ̕����������߂Ă��܂��B
2���̕�������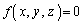 �C
�C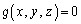 ���Ƃ��܂��B
���Ƃ��܂��B
h�Ck��K���Ȏ������Ƃ��āA
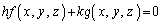 ����H
����H
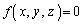 �C
�C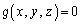
�H������\���̂́A�H��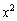 �C
�C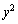 �C
�C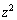 �Ƃ��������܂ނƂ��ł��B
�Ƃ��������܂ނƂ��ł��B
�H�����ʂ�\���̂́A�H��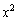 �C
�C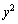 �C
�C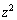 �Ƃ��������܂܂Ȃ��Ƃ��ł��B
�Ƃ��������܂܂Ȃ��Ƃ��ł��B
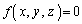 �C
�C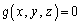 ��
��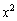 �C
�C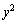 �C
�C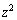 �̌W�����Ƃ���1�Ȃ�A
�̌W�����Ƃ���1�Ȃ�A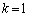 �C
�C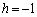 �Ƃ���A�H����
�Ƃ���A�H����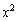 �C
�C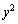 �C
�C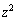 �̍����������Ƃ��ł��܂��B
�̍����������Ƃ��ł��܂��B
�܂�A
�́A2���̌��~���܂ޕ��ʂ�\���܂��B��L�ł́A���ʂ̕������B�����߂�̂ɁA���̋Z�I���g���Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 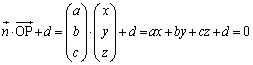
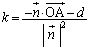
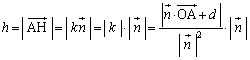
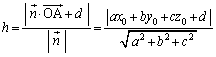 �@���(��)
�@���(��)