���嗝�n���w'02�N�O��[5]
O�����_�Ƃ���xyz��Ԃɓ_
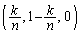 �C
�C �C���Ƃ�B�܂��Az����
�C���Ƃ�B�܂��Az����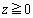 �̕����ɁA�_
�̕����ɁA�_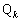 �����
�����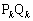 �̒�����1�ɂȂ�悤�ɂƂ�B�O�p��
�̒�����1�ɂȂ�悤�ɂƂ�B�O�p�� �̑̐ς�
�̑̐ς� �Ƃ����āA�Ɍ�
�Ƃ����āA�Ɍ�
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����Ƃ��Ă͌y�߂��敪���ϖ@�̖��ł��B
���p�O�p�` �ɂ����āA�O�����̒藝���A
�ɂ����āA�O�����̒藝���A
�� 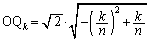
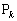
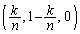 �C
�C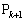
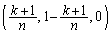 ���A
���A
�O�p�` �̖ʐρF
�̖ʐρF �@(�O�p�`�̖ʐς̌������Q��)
�@(�O�p�`�̖ʐς̌������Q��)
����āA
��ϕ�����y�Ƃ����ƁA
2�悵�Đ�������ƁA ����A
����A
�]���āA�@�̐ϕ��́A�~�A��x�����㑤�̕�����x���̊Ԃ̕����̖ʐρA�܂�A���a �̉~�A�̖ʐς�
�̉~�A�̖ʐς� �ɂȂ�܂��B
�ɂȂ�܂��B
�������āA�@�̒l�́A
�� 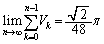 ......[��]
......[��]
�@�̐ϕ����~�̖ʐς̈ꕔ���Ƃ��ċ��߂�Z�I�́A����ł͕p�o�̕K�{�Z�I�ł��B�K���o���Ă����Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B