���嗝�n���w'02�N�O��[4]
a�͐��̎����Ƃ���Bxy���ʂ�y����ɓ_P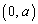 ���Ƃ�B��
���Ƃ�B��
�̃O���t��C�Ƃ���BC��̓_Q�Ŏ��̏����������̂����_O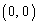 �ȊO�ɑ��݂���悤��a�͈̔͂����߂�B
�ȊO�ɑ��݂���悤��a�͈̔͂����߂�B
�����FQ�ɂ�����C�̐ڐ�������PQ�ƒ�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����ɂ́A����PQ��C���ڐ��ƒ�������A�Ə����Ă���܂����AQ�ɂ�����C�̐ڐ��Ɛ����ł�����Q��ʂ钼���́A���̓_Q�ɂ�����C���@���ł��B
�]���āA����PQ��C�̖@���ƂȂ肤��̂����l����悢�킯�ł��B
�܂��AQ��x���W��t�Ƃ��āAQ�ɂ�����@�������߂Ă݂܂��BQ��y���W��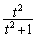 �ł��B
�ł��B
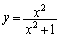 �̗��ӂ��������ƁA
�̗��ӂ��������ƁA
���_�ȊO��Q���l����̂ŁA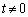 �Ƃ��čl���܂��B
�Ƃ��čl���܂��B
Q�ɂ�����@���̌X���́A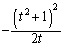 �@(�ڐ��Ɩ@���̌������Q��)
�@(�ڐ��Ɩ@���̌������Q��)
����āAQ�ɂ�����@���F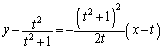
��������ƁA
�@����y�ؕЂ́A
�ł��B
���āA�uQ�ɂ�����C�̐ڐ�������PQ�ƒ�������B�v�悤�ȓ_Q�����_�ȊO�ɑ��݂���A�Ƃ������Ƃ́A�ǂ��������Ƃ��ƌ����ƁAy����̓_P��ʂ�悤��C�̖@����C��̂ǂ����̓_(�ǂ��ɂȂ邩�͂킩��܂���ǁA���_�ȊO�̓_�ł�)��ړ_�Ƃ��Ĉ�����A�Ƃ������Ƃł��B
a�́AP��y���W�Ȃ̂ŁA�@����y�ؕЂɂȂ�܂��B
C��̓_Q�����݂��邽�߂�a�͈̔͂Ƃ͉����ƌ����ƁAC��̂�����_�Ŗ@���������Ă݂��Ƃ��āA�@����y���Ƃ̌�_P��y��������܂����A���̌�_P��y���W�A�܂��@����y�ؕЂ��Ƃ肤��͈��Ƃ����Ӗ��ł��B
�����̕����̃��W�b�N����₱�����ł����A���̖��́A�����ȊO�͒P���Ȕ����ϕ��̌v�Z���Ȃ̂ŁA�O���t��`���Ė@�������낢��Ə�������ōl���Ă݂Ă��������B
���ǁA��������悢�̂��ƌ����ƁA�@��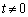 �Ƃ��čl������
�Ƃ��čl������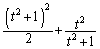 �̎�蓾��l�͈̔͂����߂�悢�A�Ƃ������Ƃł��B
�̎�蓾��l�͈̔͂����߂�悢�A�Ƃ������Ƃł��B
���āA���̊������̂܂ܔ������Ēl������߂Ă��ǂ��̂ł����A�ʕ����ēW�J��������ƁA������Ǝ��Ԃ������肻���ł��B�����ŁA�v�Z�̍H�v���l���܂��B
���̎��ł́A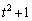 ��2��o�Ă��܂��B
��2��o�Ă��܂��B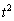 �Ƃ�������������܂����A�����
�Ƃ�������������܂����A�����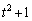 ����1�����������̂��Ƃł��B
����1�����������̂��Ƃł��B
����ƁA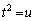 �ƒu�����̂ł́A���ꂪ
�ƒu�����̂ł́A���ꂪ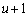 �ƂȂ��āA���̔����@���g���Ƃ��낪���ʓ|�ɂȂ�܂��B
�ƂȂ��āA���̔����@���g���Ƃ��낪���ʓ|�ɂȂ�܂��B
�]���āA�����́A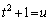 �ƒu���Au�̊��Ƃ��Ēl����l����̂��őP�ł��B
�ƒu���Au�̊��Ƃ��Ēl����l����̂��őP�ł��B
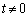 �̂Ƃ��A
�̂Ƃ��A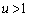 �ł��B
�ł��B
�Ƃ����āA��������ƁA
����āA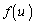 �́A
�́A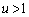 �ɂ������P���������ł��B
�ɂ������P���������ł��B
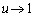 �̂Ƃ��A
�̂Ƃ��A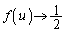
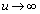 �̂Ƃ��A
�̂Ƃ��A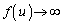
������A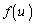 �̒l��́A
�̒l��́A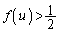 �ł��B
�ł��B
�����A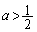 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B