���嗝�n���w'02�N�O��[2]
n�͐��̐����Ƃ���B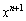 ��
�� �Ŋ������]���
�Ŋ������]���
�Ƃ����B
�������Ƃ������B
(2)  �ɑ��āA
�ɑ��āA �C
�C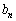 �͋��ɐ��̐����ŁA�݂��ɑf�ł��邱�Ƃ��ؖ�����B
�͋��ɐ��̐����ŁA�݂��ɑf�ł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������̏��Z�����w�I�A�[�@�̗Z�����ł��B(2)�ł́A�����������ł��܂����A�w���@��p���邱�Ƃŏؖ����ł��܂��B
�Ȃ��A���̖��œo�ꂷ�鐔��́A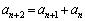 �����A����ŕp�o�̃t�B�{�i�b�`�̐���ł��B
�����A����ŕp�o�̃t�B�{�i�b�`�̐���ł��B
(1) ��ӂ��A �ɑ��āA
�ɑ��āA �Ƃ������Ƃ��ł��܂��B
�����ŁA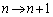 �Ƃ���ƁA
�Ƃ���ƁA 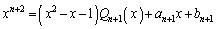 ����A
����A
�@���ӂ�x�������ĕό`���܂��B
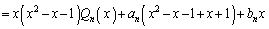
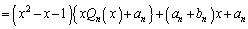 ����B
����B�A�́A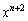 ��
��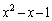 �Ŋ������]�肪
�Ŋ������]�肪 ���ƌ����Ă��܂��B
���ƌ����Ă��܂��B
�B�́A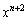 ��
��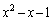 �Ŋ������]�肪
�Ŋ������]�肪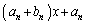 ���ƌ����Ă��܂��B
���ƌ����Ă��܂��B
�A�C�B���r���邱�Ƃɂ��A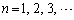 �ɑ��āA
�ɑ��āA 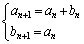 ����C
����C
i)  �̂Ƃ��A
�̂Ƃ��A �@�ɂ����āA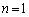 �Ƃ���ƁA
�Ƃ���ƁA ���A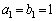
����āA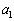 �C
�C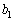 �͋��ɐ��̐����ŁA�݂��ɑf(�ő����1)�ł��B
�͋��ɐ��̐����ŁA�݂��ɑf(�ő����1)�ł��B
ii) 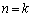 �̂Ƃ��A���藧�Ƃ��āA
�̂Ƃ��A���藧�Ƃ��āA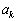 �C
�C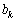 �͋��ɐ��̐����ŁA�݂��ɑf�ł��B ����D
�͋��ɐ��̐����ŁA�݂��ɑf�ł��B ����D ���̂Ƃ��A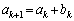 �C
�C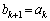 �����ɐ��̐����ł��B
�����ɐ��̐����ł��B
�����ŁA �C
�C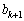 ���݂��ɑf�ł͂Ȃ��Ɖ��肵�܂��B ����E�@(�w���@�ɂ��ẮA�ؖ��̋Z�I���Q��)����ƁA
���݂��ɑf�ł͂Ȃ��Ɖ��肵�܂��B ����E�@(�w���@�ɂ��ẮA�ؖ��̋Z�I���Q��)����ƁA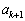 �C
�C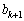 ��2�ȏ�̌���s�����͂��ł��B
��2�ȏ�̌���s�����͂��ł��B
���̂Ƃ��Ap�Cq�𐳂̐����Ƃ��āA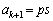 �C
�C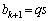 �Ƃ������Ƃ��ł��܂��B�C���A
�Ƃ������Ƃ��ł��܂��B�C���A  �ł�����A
�ł�����A ��
��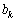 ��2�ȏ�̌���s�������ƂɂȂ�A
��2�ȏ�̌���s�������ƂɂȂ�A �C
�C ���݂��ɑf�ł���Ƃ������w�I�A�[�@�̉���D�Ɩ������܂��B
���݂��ɑf�ł���Ƃ������w�I�A�[�@�̉���D�Ɩ������܂��B
�]���āA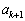 �C
�C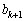 ���݂��ɑf�ł͂Ȃ��Ƃ�������E�͌��ŁA
���݂��ɑf�ł͂Ȃ��Ƃ�������E�͌��ŁA �C
�C �݂͌��ɑf�ł��B
�݂͌��ɑf�ł��B����āA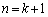 �̂Ƃ������藧���܂��B1)�Cii)���A
�̂Ƃ������藧���܂��B1)�Cii)���A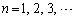 �ɑ��āA
�ɑ��āA �C
�C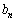 �͋��ɐ��̐����ŁA�݂��ɑf�ł��邱�Ƃ�������܂����B(�ؖ��I)
�͋��ɐ��̐����ŁA�݂��ɑf�ł��邱�Ƃ�������܂����B(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B