東大文系数学'05年前期[1]
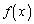を
を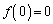みたす2次関数とする。a，bを実数として、関数
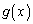を次で与える。
a，bをいろいろ変化させ
が最小になるようにする。
このとき、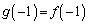
，
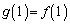であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答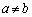 
のとき、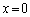
においては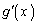
が存在しません。こういう入試問題があるので、定積分
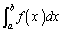のa，bを「下端」、「上端」と呼ぶべきではなく、「下限」、「上限」と呼ぶべきだと私は思います。'90年代以降の「ゆとり教育」教科書改訂はすべて白紙に戻して、'90年代以前に戻すべきだ、と、私は主張します。
文系数学でこうした出題をするということは、ひょっとして、出題者にも、そういう考えの人材を文科省に送り込もうという魂胆があるのでしょうか？
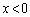において、
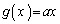より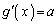
(微分・導関数を参照)
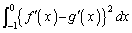(定積分を参照)
同様に、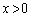
において、
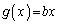より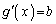
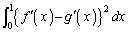
よって、
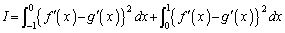
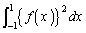は定数なので、Iは、
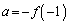かつ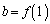
のときに最小です(2次関数を参照)。
，
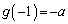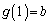より、Iが最小のとき、
，
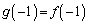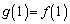
注．抽象的関数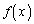
のまま計算しないで、
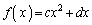として具体的な形を入れて計算しても、ほぼ同様に結論が得られます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(∵ 
)
