���嗝�n���w'06�N�O��[4]
���̏��������g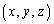 ���l����B
���l����B
����(A)�Fx�Cy�Cz�͐��̐�����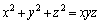 �����
�����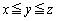 �����B
�����B �ȉ��̖₢�ɓ�����B
(1) ����(A)�����g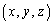 ��
��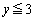 �ƂȂ���̂����ׂċ��߂�B
�ƂȂ���̂����ׂċ��߂�B (2) �g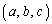 ������(A)�����Ƃ���B���̂Ƃ��A�g
������(A)�����Ƃ���B���̂Ƃ��A�g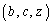 ������(A)�����悤��z�����݂��邱�Ƃ������B
������(A)�����悤��z�����݂��邱�Ƃ������B (3) ����(A)�����g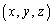 �́A�����ɑ��݂��邱�Ƃ������B
�́A�����ɑ��݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ƃ肽�Ăē��Ƃ����قǂł͂���܂��A�������ŁA�ǂꂾ����Âɍl���邱�Ƃ��ł��邩�A�Ƃ������ł��B
(1) �E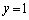 �̂Ƃ��A
�̂Ƃ��A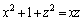
�� 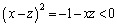
��������A���̐���x�Cz�͑��݂��܂���B
�E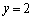 �̂Ƃ��A
�̂Ƃ��A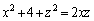
�� 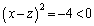
��������A���̐���x�Cz�͑��݂��܂���B
�E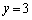 �̂Ƃ��A
�̂Ƃ��A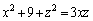
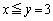 ���A
���A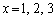 �Ɍ����܂��B
�Ɍ����܂��B
i) 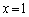 �̂Ƃ��A
�̂Ƃ��A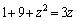
����������̐���z�͑��݂��܂���B
ii) 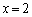 �̂Ƃ��A
�̂Ƃ��A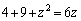
����������̐���z�͑��݂��܂���B
iii) 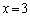 �̂Ƃ��A
�̂Ƃ��A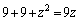
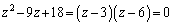 ��
�� 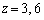
�ȏ���A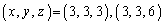 ......[��]
......[��]
(2) �g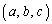 ������(A)�����̂ŁA
������(A)�����̂ŁA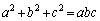 �@����@�@���������܂��B
�@����@�@���������܂��B ���̂Ƃ��A�g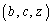 ������(A)�����Ȃ�A
������(A)�����Ȃ�A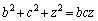 �����藧�͂��ł��B
�����藧�͂��ł��B
���̂Ƃ��A�@���A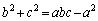 �C����āA
�C����āA �� 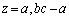
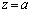 ��
��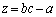 �ɂ��āA
�ɂ��āA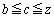 �ł��邱�Ƃ�������Ηǂ��̂ł����A
�ł��邱�Ƃ�������Ηǂ��̂ł����A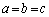 �̏ꍇ�ƁA����ȊO�̏ꍇ�Ƃŕ����Ē��ׂ܂��B
�̏ꍇ�ƁA����ȊO�̏ꍇ�Ƃŕ����Ē��ׂ܂��B�E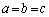 �ł���A
�ł���A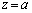 �Ƃ��āA����(A)�����g
�Ƃ��āA����(A)�����g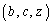 �����݂��܂��B
�����݂��܂��B �E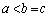 �܂��́A
�܂��́A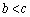 �ł���ꍇ�A(1)���A
�ł���ꍇ�A(1)���A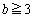 �䂦�A
�䂦�A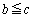 �̗��ӂ�
�̗��ӂ�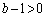 �������āA
�������āA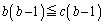
�� 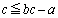 �@����A
�@����A ����āA�g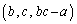 �͏���(A)�����܂��B
�͏���(A)�����܂��B
�ȏ���A�g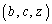 ������(A)�����悤��z�����݂��܂��B
������(A)�����悤��z�����݂��܂��B
(3) 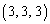 ����o�����āA�g
����o�����āA�g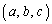 ����g
����g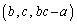 �����߂�Ƃ����菇�ŁA����(A)�����g
�����߂�Ƃ����菇�ŁA����(A)�����g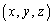 �����X�ɋ��߂Ă������Ƃ��܂��B
�����X�ɋ��߂Ă������Ƃ��܂��B ���ۂɋ��߂Ă����ƁA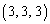 ��
��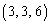 ��
��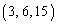 ��
��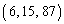 ��
��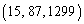 ��
��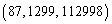 �ƂȂ��Ă����܂��B
�ƂȂ��Ă����܂��B
����(A)�����An�Ԗڂ̑g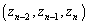 (
(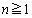 )�����݂��邱�Ƃ����w�I�A�[�@�ɂ�莦���܂��B
)�����݂��邱�Ƃ����w�I�A�[�@�ɂ�莦���܂��B �E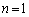 �̂Ƃ��A
�̂Ƃ��A 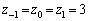 �Ƃ���A(1)�ɂ��A1�Ԗڂ̑g
�Ƃ���A(1)�ɂ��A1�Ԗڂ̑g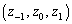 �����݂��܂��B
�����݂��܂��B �E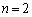 �̂Ƃ��A
�̂Ƃ��A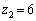 �Ƃ���A(1)�ɂ��A2�Ԗڂ̑g
�Ƃ���A(1)�ɂ��A2�Ԗڂ̑g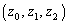 �����݂��܂��B
�����݂��܂��B �E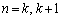 �̂Ƃ��A����(A)�����g
�̂Ƃ��A����(A)�����g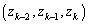 �C
�C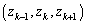 �����݂���Ɖ��肵�܂��B
�����݂���Ɖ��肵�܂��B 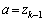 �C
�C �C
�C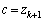 �Ƃ��āA(2)���A
�Ƃ��āA(2)���A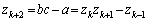 �Ƃ���A����(A)�����g
�Ƃ���A����(A)�����g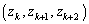 �����݂��܂��B
�����݂��܂��B
����āA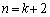 �̂Ƃ����A����(A)�����An�Ԗڂ̑g
�̂Ƃ����A����(A)�����An�Ԗڂ̑g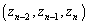 �����݂��܂��B
�����݂��܂��B���w�I�A�[�@�ɂ��A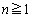 �ƂȂ鐮��n�ɑ��āA����(A)�����An�Ԗڂ̑g
�ƂȂ鐮��n�ɑ��āA����(A)�����An�Ԗڂ̑g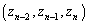 �����݂��܂��B
�����݂��܂��B
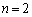 �̏ꍇ�ɁA(2)�̒��ŁA
�̏ꍇ�ɁA(2)�̒��ŁA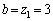 �C
�C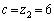 �Ƃ��āA
�Ƃ��āA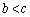 ���A
���A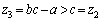 �ł���A
�ł���A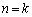 �̂Ƃ��ɁA(2)�̒��ŁA
�̂Ƃ��ɁA(2)�̒��ŁA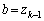 �C
�C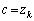 �Ƃ��āA
�Ƃ��āA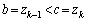 �ł���A
�ł���A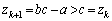 (�A�̕s�����̓������������Ƃ��ł���)
(�A�̕s�����̓������������Ƃ��ł���)�]���āA���ׂĂ�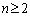 �ɂ��āA
�ɂ��āA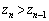
�ȏ���A���ׂĂ�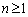 �ɂ��āA����(A)�����g
�ɂ��āA����(A)�����g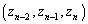 �͈قȂ�܂��B
�͈قȂ�܂��B
���̐����͖����ɑ��݂���̂ŁA����(A)�����g�������ɑ��݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B