東京大学理系2006年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] Oを原点とする座標平面上の4点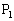 ,
,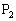 ,
,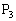 ,
,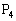 で、条件
で、条件
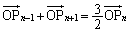 (
(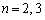 )
)
(1) 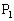 ,
,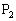 が曲線
が曲線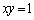 上にあるとき、
上にあるとき、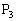 はこの曲線上にはないことを示せ。
はこの曲線上にはないことを示せ。
(2) 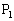 ,
,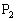 ,
,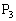 が円周
が円周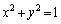 上にあるとき、
上にあるとき、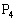 もこの円周上にあることを示せ。
もこの円周上にあることを示せ。
[解答へ]
[2] コンピュータの画面に、記号○と×のいずれかを表示させる操作をくり返し行う。このとき、各操作で、直前の記号と同じ記号を続けて表示する確率は、それまでの経過に関係なく、pであるとする。
最初に、コンピュータの画面に記号×が表示された。操作をくり返し行い、記号×が最初のものも含めて3個出るよりも前に、記号○がn個出る確率を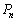 とする。ただし、記号○がn個出た段階で操作は終了する。
とする。ただし、記号○がn個出た段階で操作は終了する。
(1) 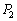 をpで表せ。
をpで表せ。 (2) 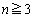 のとき、
のとき、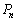 をpとnで表せ。
をpとnで表せ。 [解答へ]
[3] Oを原点とする座標平面上に、y軸上の点P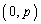 と、直線m:
と、直線m: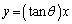 が与えられている。ここで、
が与えられている。ここで、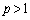 ,
,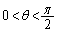 とする。
とする。
いま、傾きがαの直線lを対称軸とする対称移動を行うと、原点Oは直線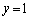 上の、第1象限の点Qに移り、y軸上の点Pは直線m上の、第1象限の点Rに移った。
上の、第1象限の点Qに移り、y軸上の点Pは直線m上の、第1象限の点Rに移った。
(1) このとき、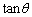 をαとpで表せ。
をαとpで表せ。 (2) 次の条件を満たす点Pが存在することを示し、そのときのpの値を求めよ。
条件:どのようなθ (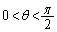 )に対しても、原点を通り直線lに垂直な直線は
)に対しても、原点を通り直線lに垂直な直線は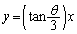 となる。
となる。 [解答へ]
[4] 次の条件を満たす組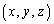 を考える。
を考える。
条件(A):x,y,zは正の整数で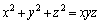 および
および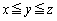 を満たす。
を満たす。 以下の問いに答えよ。
(1) 条件(A)を満たす組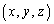 で
で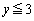 となるものをすべて求めよ。
となるものをすべて求めよ。 (2) 組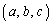 が条件(A)を満たすとする。このとき、組
が条件(A)を満たすとする。このとき、組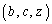 が条件(A)を満たすようなzが存在することを示せ。
が条件(A)を満たすようなzが存在することを示せ。 (3) 条件(A)を満たす組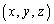 は、無数に存在することを示せ。
は、無数に存在することを示せ。 [解答へ]
[5] 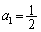 とし、数列
とし、数列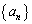 を漸化式
を漸化式
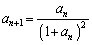 (
(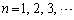 )
)
(1) 各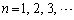 に対し、
に対し、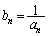 とおく。
とおく。 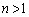 のとき、
のとき、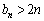 となることを示せ。
となることを示せ。(2) 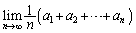 を求めよ。
を求めよ。 (3) 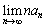 を求めよ。
を求めよ。 [解答へ]
[6] 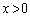 を定義域とする関数
を定義域とする関数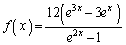 について、以下の問いに答えよ。
について、以下の問いに答えよ。
(1) 関数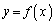 (
(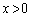 )は、実数全体を定義域とする逆関数を持つことを示せ。すなわち、任意の実数aに対して、
)は、実数全体を定義域とする逆関数を持つことを示せ。すなわち、任意の実数aに対して、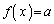 となる
となる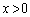 がただ1つ存在することを示せ。
がただ1つ存在することを示せ。 (2) 前問(1)で定められた逆関数を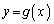 (
(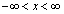 )とする。このとき、定積分
)とする。このとき、定積分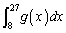 を求めよ。
を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。