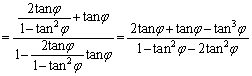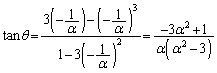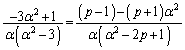���嗝�n���w'06�N�O��[3]
O�����_�Ƃ�����W���ʏ�ɁAy����̓_P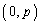 �ƁA����m�F
�ƁA����m�F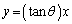 ���^�����Ă���B�����ŁA
���^�����Ă���B�����ŁA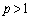 �C
�C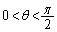 �Ƃ���B
�Ƃ���B
���܁A�X����α�̒���l��Ώ̎��Ƃ���Ώ̈ړ����s���ƁA���_O�͒���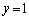 ��́A��1�ی��̓_Q�Ɉڂ�Ay����̓_P�͒���m��́A��1�ی��̓_R�Ɉڂ����B
��́A��1�ی��̓_Q�Ɉڂ�Ay����̓_P�͒���m��́A��1�ی��̓_R�Ɉڂ����B
(1) ���̂Ƃ��A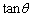 ��α��p�ŕ\���B
��α��p�ŕ\���B (2) ���̏��������_P�����݂��邱�Ƃ������A���̂Ƃ���p�̒l�����߂�B
�����F�ǂ̂悤��θ (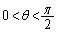 )�ɑ��Ă��A���_��ʂ蒼��l�ɐ����Ȓ�����
)�ɑ��Ă��A���_��ʂ蒼��l�ɐ����Ȓ�����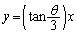 �ƂȂ�B
�ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�C�͂��[�������āA�����Ђ�����v�Z��������ł��B�Ȃ��A���W���ʂɂ�����Ώ����Q�Ƃ��Ă��������B
(1) ����l�̕�������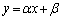 �CQ��x���W��q�CR��x���W��r�Ƃ���B
�CQ��x���W��q�CR��x���W��r�Ƃ���B ��ӂ��A ��
��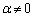 �C�܂�m��ɂȂ��_P��l�Ɋւ���Ώ̓_��m��ɗ��邱�Ƃ���A
�C�܂�m��ɂȂ��_P��l�Ɋւ���Ώ̓_��m��ɗ��邱�Ƃ���A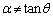
�_O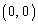 �Ɠ_Q
�Ɠ_Q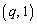 ������l�Ɋւ����Ώ�������A
������l�Ɋւ����Ώ�������A �_P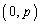 �Ɠ_R
�Ɠ_R ������l�Ɋւ��đΏ̂�����A
������l�Ɋւ��đΏ̂�����A 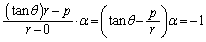 �C
�C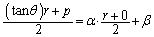
�O�҂��A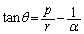 �@(
�@(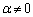 )�@����A
)�@����A
��҂���@�������āA ������A�ɑ������ƁA
������āA
(2) 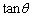 ��
��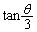 ���o�Ă���̂Ő��ڂɊւ���3�{�p�̌������Ă����܂��B
���o�Ă���̂Ő��ڂɊւ���3�{�p�̌������Ă����܂��B 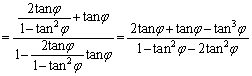
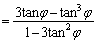 �@����B
�@����B�� 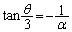 �@����C
�@����C �B�ɂ����āA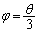 �Ƃ��āA
�Ƃ��āA (1)�̌��ʂ�p���āA
������ƁA
�W�J���Đ�������ƁA
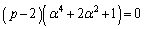 �@����Dθ ��α�̊Ԃɂ́A�C�Ƃ����W������̂ŁA�D���Aθ �ɂ�����炸�A���Ȃ킿�Aα�ɂ�����炸�������邽�߂ɂ́A
�@����Dθ ��α�̊Ԃɂ́A�C�Ƃ����W������̂ŁA�D���Aθ �ɂ�����炸�A���Ȃ킿�Aα�ɂ�����炸�������邽�߂ɂ́A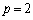 ......[��]
......[��]�_P��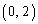 �Ƃ���A�C�ӂ�θ (
�Ƃ���A�C�ӂ�θ (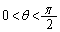 )�ɑ��ćC����������悤��α���Ƃ�A����l��
)�ɑ��ćC����������悤��α���Ƃ�A����l��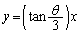 �������ɂȂ�A�^����ꂽ��������������̂ŁA�_P�͑��݂��܂��B
�������ɂȂ�A�^����ꂽ��������������̂ŁA�_P�͑��݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 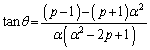 ......[��]
......[��]