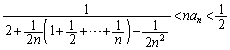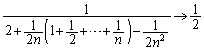���嗝�n���w'06�N�O��[5]
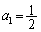 �Ƃ��A����
�Ƃ��A����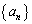 ��Q����
��Q����
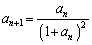 �@�@(
�@�@(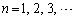 )
)
(1) �e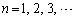 �ɑ��A
�ɑ��A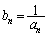 �Ƃ����B
�Ƃ����B 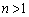 �̂Ƃ��A
�̂Ƃ��A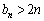 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B(2) 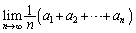 �����߂�B
�����߂�B (3) 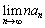 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ƃ����킯�ł͂Ȃ��ł����A����Ȃ�ɍH�v���Â炷�K�v�������Ĉ�{���ł͂���܂���B�Ȃ��������Q�Ƃ��Ă��������B
(1) 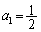 ���A
���A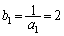 �@����@
�@����@ 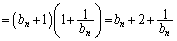 �@����B
�@����B�A���A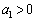 �ŁA
�ŁA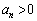 �Ȃ�
�Ȃ�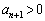 �ŋA�[�I�ɁA
�ŋA�[�I�ɁA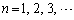 �ɑ��āA
�ɑ��āA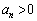 �@����C�@(���w�I�A�[�@���Q��)����āA
�@����C�@(���w�I�A�[�@���Q��)����āA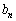 �ɂ��Ă��A
�ɂ��Ă��A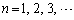 �ɑ��āA
�ɑ��āA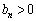
����ƁA�B���A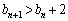
�@��p���āA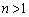 �̂Ƃ��A
�̂Ƃ��A
(2) �C���A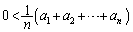 �@����D
�@����D �܂��A(1)���A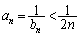
������A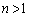 �̂Ƃ��A
�̂Ƃ��A 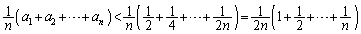 �@����E
�@����E�Ƃ���ŁA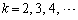 �̂Ƃ��A
�̂Ƃ��A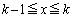 �Ȃ�x�ɂ��āA
�Ȃ�x�ɂ��āA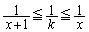
�����͍P���I�ɐ��藧�킯�ł͂Ȃ��̂ŁA  �ɂ��ĉ����A����ɁA
�ɂ��ĉ����A����ɁA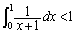 ��p���āA���ӂ�
��p���āA���ӂ�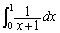 �������A���ӂƉE�ӂ�1��������ƁA
�������A���ӂƉE�ӂ�1��������ƁA�� 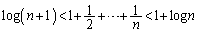
�e�ӂ�n�Ŋ���ƁA
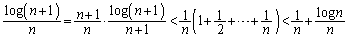 �@����F
�@����F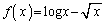 �Ƃ����ƁA
�Ƃ����ƁA�����\���A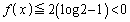
�� 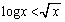
���ӂ�x�@(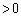 )�Ŋ���ƁA
)�Ŋ���ƁA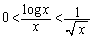
�����ŁA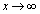 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A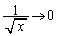
����āA�͂��݂����̌������A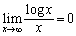
������A�F�̍��ӂƉE�ӂ́A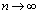 �̂Ƃ��A
�̂Ƃ��A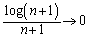 �C
�C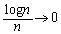 ������A�Ƃ���0�ɋ߂Â��B�͂��݂����̌������A�F�̒��ӂɂ��Ă��A
������A�Ƃ���0�ɋ߂Â��B�͂��݂����̌������A�F�̒��ӂɂ��Ă��A 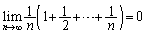 �@����G
�@����G�D�C�E��p���āA
����ɁA�͂��݂����̌������A
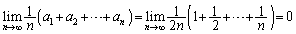 ......[��]
......[��]
(3) (1)���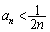 �������Ă���̂ŁA
�������Ă���̂ŁA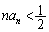 �@����H
�@����H �]���āA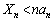 �ƂȂ�
�ƂȂ�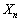 �ŁA
�ŁA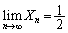 �ƂȂ���̂�T���悢�̂ł��B
�ƂȂ���̂�T���悢�̂ł��B
���̂��߂ɂ́A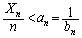 �C�܂�A
�C�܂�A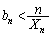 �Ƃ����`�̕s�������Ђ˂�o���Ȃ��Ƃ����܂���B
�Ƃ����`�̕s�������Ђ˂�o���Ȃ��Ƃ����܂���B
�B���Ȃ��߂Ă���ƁA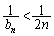 �𗘗p����A���̌`����ꂻ���ł��B
�𗘗p����A���̌`����ꂻ���ł��B
�B�ɂ����āA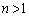 �̂Ƃ��A
�̂Ƃ��A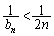 ���A
���A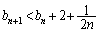
�@��p���āA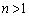 �̂Ƃ��A
�̂Ƃ��A ������A
����ƁA�H����A
�G���g���ƁA���ӂ́A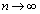 �̂Ƃ��A
�̂Ƃ��A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B