���嗝�n���w'06�N�O��[1]
O�����_�Ƃ�����W���ʏ��4�_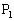 �C
�C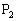 �C
�C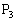 �C
�C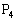 �ŁA����
�ŁA����
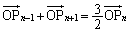 �@(
�@(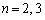 )
)
(1) 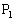 �C
�C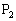 ���Ȑ�
���Ȑ�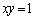 ��ɂ���Ƃ��A
��ɂ���Ƃ��A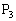 �͂��̋Ȑ���ɂ͂Ȃ����Ƃ������B
�͂��̋Ȑ���ɂ͂Ȃ����Ƃ������B
(2) 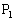 �C
�C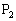 �C
�C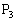 ���~��
���~��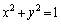 ��ɂ���Ƃ��A
��ɂ���Ƃ��A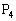 �����̉~����ɂ��邱�Ƃ������B
�����̉~����ɂ��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�]�v�Ȃ��Ƃ��l�����ɑf���Ɏ��g�߂Α債�����Ƃ͂���܂���B
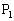 �C
�C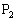 ���Ȑ�
���Ȑ�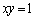 ��ɂ���Ƃ��A
��ɂ���Ƃ��A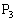 �����̋Ȑ���ɂ���Ɖ��肵�܂��B
�����̋Ȑ���ɂ���Ɖ��肵�܂��B
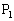 �C
�C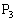 ��x���W��p�Cq�Ƃ���ƁA���ꂼ���y���W��
��x���W��p�Cq�Ƃ���ƁA���ꂼ���y���W��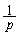 �C
�C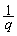 �ł��B
�ł��B
�^����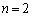 �Ƃ��āA
�Ƃ��āA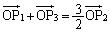 ���A
���A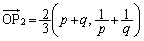 �@����@
�@����@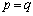 �̏ꍇ�A
�̏ꍇ�A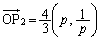 �ł����A
�ł����A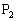
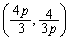 ��
��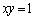 �������A
�������A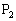 �͋Ȑ�
�͋Ȑ�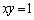 ��̓_�ł͂���܂���B����A
��̓_�ł͂���܂���B����A
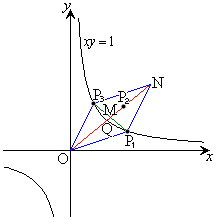
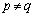 �̏ꍇ�A
�̏ꍇ�A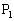 �C
�C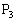 ���Ƃ��ɑ�1�ی��̓_�ŁA
���Ƃ��ɑ�1�ی��̓_�ŁA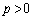 �C
�C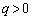 ���Ƃ��܂��B�@���A
���Ƃ��܂��B�@���A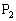 ����1�ی��̓_�ł��B
����1�ی��̓_�ł��B
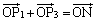 �Ƃ��āA���s�l�ӌ`�̑Ίp��ON��
�Ƃ��āA���s�l�ӌ`�̑Ίp��ON��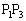 �݂͌��ɑ��������A����ON�̒��_M�͐���
�݂͌��ɑ��������A����ON�̒��_M�͐���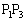 ��̓_�ł��B
��̓_�ł��B
�Ƃ���ŁA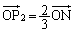 ���A
���A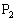 �͐���MN���M�ȊO�̓_�ł��B
�͐���MN���M�ȊO�̓_�ł��B
�Ȑ�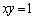 �͑�1�ی��ɂ����ĉ��ɓʂȋȐ��Ȃ̂ŁA�Ȑ�
�͑�1�ی��ɂ����ĉ��ɓʂȋȐ��Ȃ̂ŁA�Ȑ�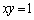 �Ɛ���ON�Ƃ̌�_Q�͐���
�Ɛ���ON�Ƃ̌�_Q�͐���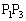 �̉����ɗ��܂��B����āAQ�͐���OM���M�ȊO�̓_�ł��B
�̉����ɗ��܂��B����āAQ�͐���OM���M�ȊO�̓_�ł��B
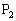 �͐���MN���M�ȊO�̓_�ŁCQ�͐���OM���M�ȊO�̓_�Ȃ̂ŁA���҂���v���邱�Ƃ͂���܂���B����́A
�͐���MN���M�ȊO�̓_�ŁCQ�͐���OM���M�ȊO�̓_�Ȃ̂ŁA���҂���v���邱�Ƃ͂���܂���B����́A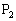 ���Ȑ�
���Ȑ�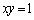 ��̓_�ł͂Ȃ����Ƃ��Ӗ����Ă��܂��B����B
��̓_�ł͂Ȃ����Ƃ��Ӗ����Ă��܂��B����B
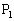 �C
�C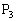 ���Ƃ��ɑ�3�ی��̓_�ł���ꍇ�ɂ́A���_�Ɋւ��đΏۂȈʒu��
���Ƃ��ɑ�3�ی��̓_�ł���ꍇ�ɂ́A���_�Ɋւ��đΏۂȈʒu��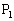 �C
�C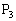 ���ڂ��čl����A�B�ɂ��A
���ڂ��čl����A�B�ɂ��A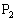 �͋Ȑ�
�͋Ȑ�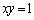 ��̓_�ł͂���܂���B����C
��̓_�ł͂���܂���B����C
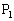 �C
�C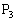 ���������1�ی��ő�������3�ی��ɂ����āAp�Cq���ٕ������Ƃ��܂��B�@���A
���������1�ی��ő�������3�ی��ɂ����āAp�Cq���ٕ������Ƃ��܂��B�@���A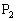
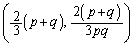 ��x���W��y���W�́A
��x���W��y���W�́A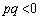 �ɂ��A�ٕ����ł����āA�Ȑ�
�ɂ��A�ٕ����ł����āA�Ȑ�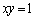 �͑�1�ی��Ƒ�3�ی��ɂ������݂��Ȃ��̂ŁA
�͑�1�ی��Ƒ�3�ی��ɂ������݂��Ȃ��̂ŁA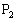 �͋Ȑ�
�͋Ȑ�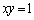 ��̓_�ł͂���܂���B����D
��̓_�ł͂���܂���B����D
�A�C�B�C�C�C�D���A�S�Ă̏ꍇ�ɂ����āA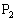 �͋Ȑ�
�͋Ȑ�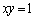 ��̓_�ł͂���܂���B
��̓_�ł͂���܂���B
����́A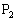 ���Ȑ�
���Ȑ�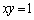 ��̓_�ł���Ƃ����O������Ɩ������܂��B
��̓_�ł���Ƃ����O������Ɩ������܂��B
����āA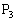 ���Ȑ�
���Ȑ�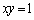 ��ɂ���Ƃ�������͌��ł����āA
��ɂ���Ƃ�������͌��ł����āA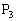 �͂��̋Ȑ���̓_�ł͂���܂���B
�͂��̋Ȑ���̓_�ł͂���܂���B
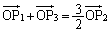 ���A
���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B