東大理系数学'06年前期[6]
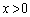 を定義域とする関数
を定義域とする関数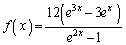 について、以下の問いに答えよ。
について、以下の問いに答えよ。
(1) 関数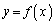 (
(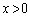 )は、実数全体を定義域とする逆関数を持つことを示せ。すなわち、任意の実数aに対して、
)は、実数全体を定義域とする逆関数を持つことを示せ。すなわち、任意の実数aに対して、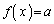 となる
となる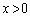 がただ1つ存在することを示せ。
がただ1つ存在することを示せ。 (2) 前問(1)で定められた逆関数を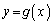 (
(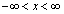 )とする。このとき、定積分
)とする。このとき、定積分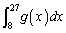 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 逆関数と言っても、元の関数とグラフのx軸,y軸が逆になるというだけなので、怖がらないようにしましょう。
分子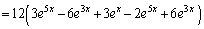
よって、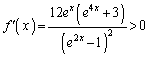 (
(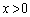 )よって、
)よって、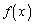 は
は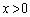 において、単調増加な関数です。
において、単調増加な関数です。
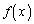 の分子は
の分子は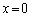 のとき
のとき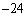 ですが、
ですが、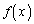 の分母は
の分母は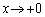 とするとき、正の数として0に近づくので、
とするとき、正の数として0に近づくので、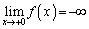
また、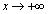 のとき、
のとき、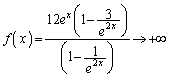 より、
より、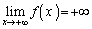
以上より、任意の実数aに対して、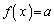 となる
となる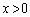 がただ1つ存在し、
がただ1つ存在し、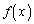 は実数全体を定義域とする逆関数をもちます。
は実数全体を定義域とする逆関数をもちます。
(2) 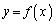 の逆関数
の逆関数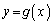 のグラフは、
のグラフは、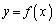 のグラフと直線
のグラフと直線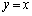 に関して対称で、
に関して対称で、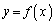 のグラフのx軸とy軸を逆にしたものと考えることができます。
のグラフのx軸とy軸を逆にしたものと考えることができます。 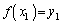 のとき、
のとき、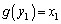 という関係があります。
という関係があります。
求める定積分は、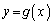 のグラフの
のグラフの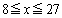 の部分とx軸との間に挟まれた部分の面積です(定積分と面積を参照)。
の部分とx軸との間に挟まれた部分の面積です(定積分と面積を参照)。
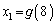 ,
,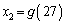 となる
となる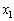 ,
,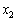 について、
について、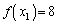 ,
,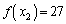 が成り立ちます。
が成り立ちます。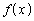 の定義域が
の定義域が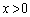 であることから、
であることから、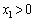 ,
,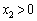 であることに注意してください。
であることに注意してください。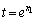 (
(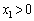 より
より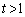 )とおいて、
)とおいて、分母を払って整理すると、
このうち、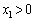 に適するものは、
に適するものは、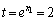
∴ 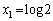
分母を払って整理すると、
このうち、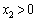 に適するものは、
に適するものは、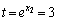
∴ 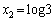
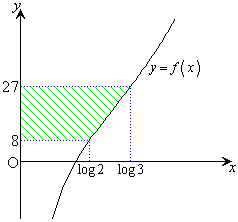 以上より、求める定積分は、
以上より、求める定積分は、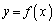 のグラフの
のグラフの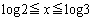 の部分とy軸との間に挟まれた部分(右図斜線部)の面積に相当します。
の部分とy軸との間に挟まれた部分(右図斜線部)の面積に相当します。
この面積は、原点O,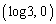 ,
,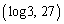 ,
,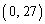 の4点を頂点とする長方形の面積から、原点O,
の4点を頂点とする長方形の面積から、原点O,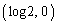 ,
,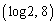 ,
,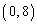 の4点を頂点とする長方形の面積と、
の4点を頂点とする長方形の面積と、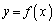 のグラフの
のグラフの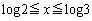 の部分とx軸の間に挟まれた部分の面積を除いた面積に相当します。よって、
の部分とx軸の間に挟まれた部分の面積を除いた面積に相当します。よって、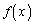 の積分について(置換積分法を参照)は、
の積分について(置換積分法を参照)は、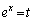 とおくと、
とおくと、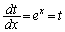 より、
より、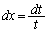 x:
x: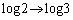 のとき、t:
のとき、t: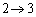
∴ 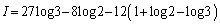
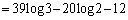 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 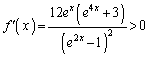 (
(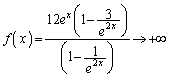 より、
より、