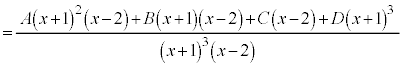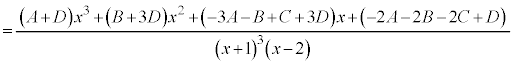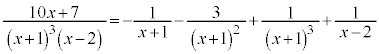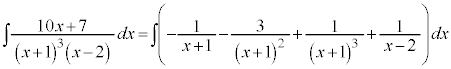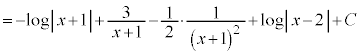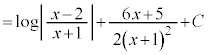分数関数の積分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
n次のxの整式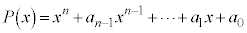 (
(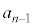 ,・・・,
,・・・,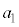 ,
,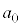 は実数)があるときに、これを実数の範囲で因数分解して、
は実数)があるときに、これを実数の範囲で因数分解して、
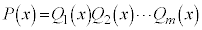 (
(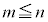 )
)
になったとします。
方程式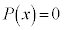 の解は以下のいずれかに限られます。
の解は以下のいずれかに限られます。
(i) 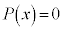 が虚数解αをもてば、それと共役な複素数
が虚数解αをもてば、それと共役な複素数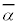 もまた解になります(高次方程式を参照)。このとき、
もまた解になります(高次方程式を参照)。このとき、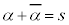 ,
,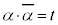 ともに実数なので、
ともに実数なので、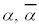 を2解にもつ2次方程式:
を2解にもつ2次方程式: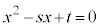 は、実数係数の方程式(ただし、判別式:
は、実数係数の方程式(ただし、判別式: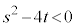 )であり、
)であり、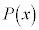 は
は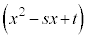 を因数にもちます。
を因数にもちます。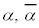 がk重解である場合には、
がk重解である場合には、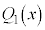 ,
,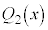 ,・・・,
,・・・,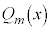 の中のどれか1つが、
の中のどれか1つが、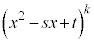 (
(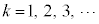 )になります。
)になります。
(iii) 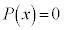 が実数の解αをもつ場合には、
が実数の解αをもつ場合には、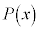 は
は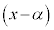 を因数にもちます。αがk重解である場合には、
を因数にもちます。αがk重解である場合には、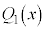 ,
,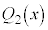 ,・・・,
,・・・,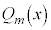 の中のどれか1つが
の中のどれか1つが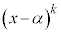 ((
((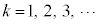 ))になります。
))になります。
従って、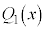 ,
,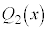 ,・・・,
,・・・,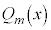 は、
は、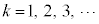 ,
,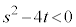 として、
として、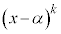 ,
,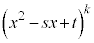 のいずれかの形をしています。
のいずれかの形をしています。
このとき、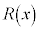 をn次未満の実数係数の整式だとして(n次以上の場合には割り算を実行すれば、整式+
をn次未満の実数係数の整式だとして(n次以上の場合には割り算を実行すれば、整式+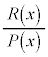 の形に直せます)、
の形に直せます)、
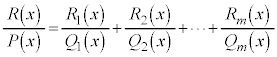 (*)
(*)
が成り立つように、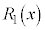 ,
,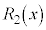 ,・・・,
,・・・,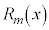 を決めることにより、
を決めることにより、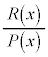 を複数の分数の和の形に直すことを部分分数分解と言います。
を複数の分数の和の形に直すことを部分分数分解と言います。
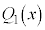 ,
,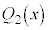 ,・・・,
,・・・,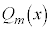 の中に、
の中に、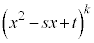 のkが2以上のものがあっても、分数関数
のkが2以上のものがあっても、分数関数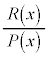 の積分の計算は可能なのですが、非常に複雑なので、ここでは、
の積分の計算は可能なのですが、非常に複雑なので、ここでは、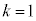 に限って考えることにします。
に限って考えることにします。
以下のように、未定係数法という技巧を用いて、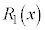 ,
,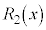 ,・・・,
,・・・,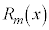 を決めます。
を決めます。
整数jが、1からmの中のどれかだとして、
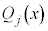 が
が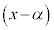 の形をしている場合には、
の形をしている場合には、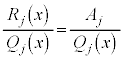 (定数)
(定数)
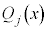 が
が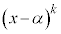 の形をしている場合には、
の形をしている場合には、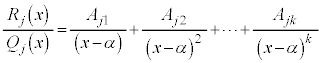 (
(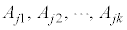 は定数)
は定数)
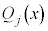 が
が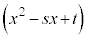 (
(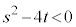 )の形をしている場合には、
)の形をしている場合には、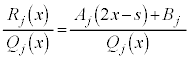 (
(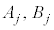 は定数)
は定数)
とおいて、(*)が成り立つように、各定数の値を定めます。
これで、部分分数分解をしたときに出てくる項は、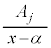 ,
,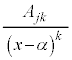 ,
,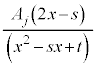 ,
,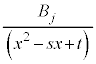 の4通りのどれかに限られます。
の4通りのどれかに限られます。
分数関数の積分: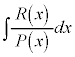 を計算する場合に、
を計算する場合に、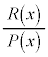 を部分分数分解すると、分解したときに出てくる項の積分は以下のどれかになり、積分の計算を行うことができます。積分定数を省略して書きますが、
を部分分数分解すると、分解したときに出てくる項の積分は以下のどれかになり、積分の計算を行うことができます。積分定数を省略して書きますが、
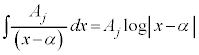 (不定積分の公式を参照)
(不定積分の公式を参照)
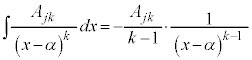 (不定積分の公式を参照)
(不定積分の公式を参照)
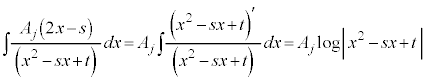 (不定積分の公式を参照)
(不定積分の公式を参照)
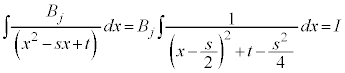 とおきます。
とおきます。
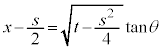 とおく(置換積分(その2)を参照)と、
とおく(置換積分(その2)を参照)と、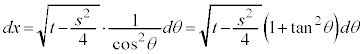 より、
より、
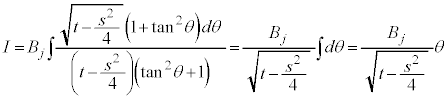
上記ではわかりにくいので、以下に代表的なパターンを例示します。
例1. 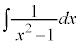
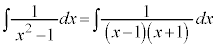
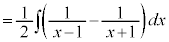
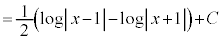
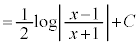
例2. 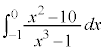
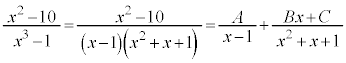 とおくと、
とおくと、
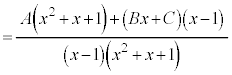
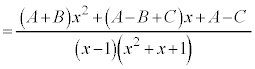
よって、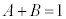 ,
,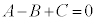 ,
,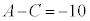
これらを解いて、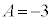 ,
,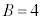 ,
,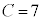
これより、
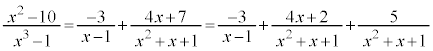
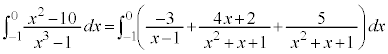
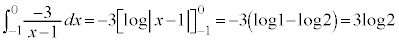
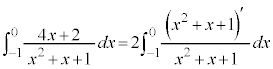
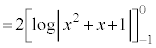
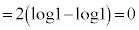
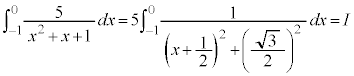
ここで、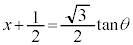 とおくと、
とおくと、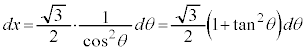
x: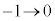 のとき、θ :
のとき、θ :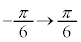
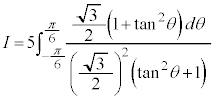
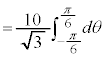
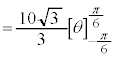
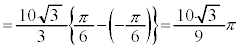
よって、
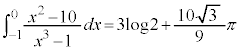
例3. 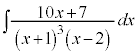
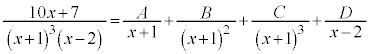 とおくと、
とおくと、
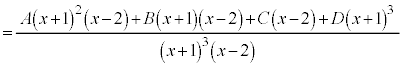
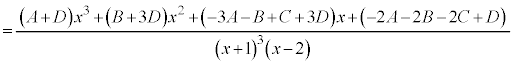
よって、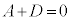 ,
,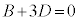 ,
,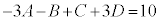 ,
,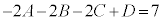
これらを解いて、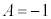 ,
,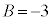 ,
,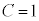 ,
,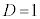
これより、
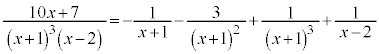
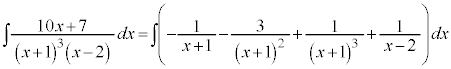
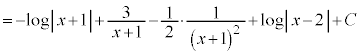
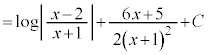
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 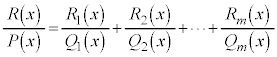 (*)
(*)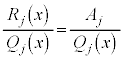 (定数)
(定数)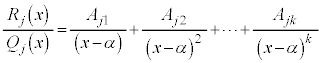 (
(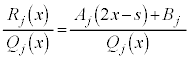 (
(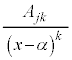 ,
,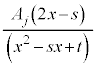 ,
,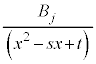 の4通りのどれかに限られます。
の4通りのどれかに限られます。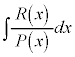 を計算する場合に、
を計算する場合に、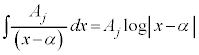 (不定積分の公式を参照)
(不定積分の公式を参照)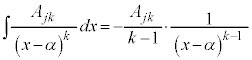 (不定積分の公式を参照)
(不定積分の公式を参照)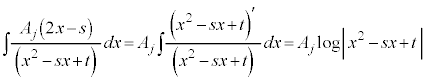 (不定積分の公式を参照)
(不定積分の公式を参照)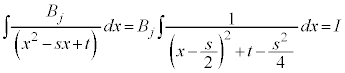 とおきます。
とおきます。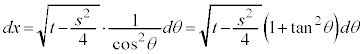 より、
より、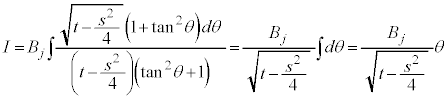
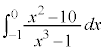
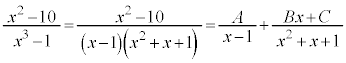 とおくと、
とおくと、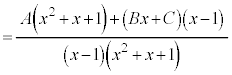
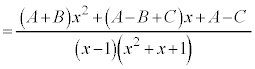
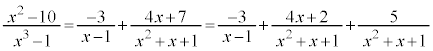
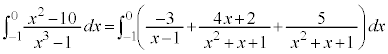
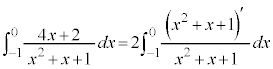
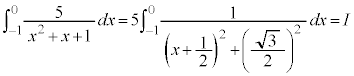
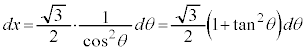
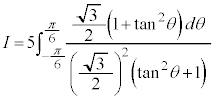
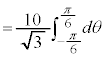
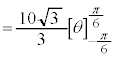
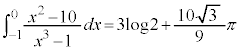
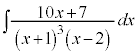
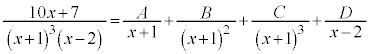 とおくと、
とおくと、