東大理系数学'07年前期[1]
nとkを正の整数とし、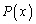 を次数がn以上の整式とする。整式
を次数がn以上の整式とする。整式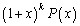 のn次以下の項の係数がすべて整数ならば、
のn次以下の項の係数がすべて整数ならば、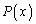 のn次以下の項の係数は、すべて整数であることを示せ。ただし、定数項については、項それ自身を係数とみなす。
のn次以下の項の係数は、すべて整数であることを示せ。ただし、定数項については、項それ自身を係数とみなす。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 素直に数学的帰納法で考える場合には、kについての帰納法にするのが最もラクなようです。
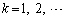 とし、nを固定して考えます。
とし、nを固定して考えます。
これのn次以下の項の係数がすべて整数、つまり、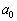 ,
,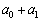 ,
,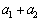 ,・・・,
,・・・,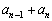 がすべて整数だとすると、
がすべて整数だとすると、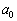 ,
,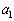 ,
,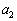 ,・・・,
,・・・,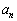 はすべて整数です。
はすべて整数です。
よって、題意が成り立ちます。
(II) 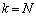 のとき、題意が成り立つとします。つまり、
のとき、題意が成り立つとします。つまり、 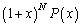 のn次以下の項がすべて整数ならば、
のn次以下の項がすべて整数ならば、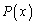 のn次以下の項の係数はすべて整数だとします。・・・(*)
のn次以下の項の係数はすべて整数だとします。・・・(*)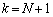 のとき、
のとき、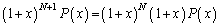 のn次以下の項がすべて整数だとすると、(*)より、
のn次以下の項がすべて整数だとすると、(*)より、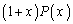 のn次以下の項の係数はすべて整数です(題意では、
のn次以下の項の係数はすべて整数です(題意では、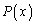 は次数がn以上の整式という制約しかないので、(*)の
は次数がn以上の整式という制約しかないので、(*)の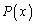 を
を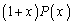 と読み替えています)。
と読み替えています)。
であれば、(I)より、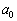 ,
,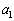 ,
,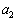 ,・・・,
,・・・,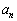 はすべて整数です。
はすべて整数です。
よって、このときも題意は成立します。
(I),(II)より、すべての正の整数kについて、題意は成立します。 (証明終)
問題文を見て、nについての帰納法にするか、kについての帰納法にするか、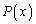 の次数についての帰納法にするか、だろうと、誰でも考えると思います。
の次数についての帰納法にするか、だろうと、誰でも考えると思います。
たぶん、合格した受験生の大半は上記の方針でやっていると思いますが、ここでは、問題の中身が見えるように、もっと、直接的に考えてみます。
二項定理: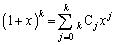 より、
より、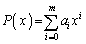 (
(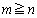 )として、
)として、
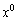 の係数は、
の係数は、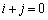 となるところから出てきますが、
となるところから出てきますが、
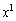 の係数は、
の係数は、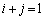 となるところから出てきますが、
となるところから出てきますが、
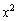 の係数は、
の係数は、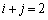 となるところから出てきますが、
となるところから出てきますが、
・・・・・・
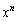 の係数は、
の係数は、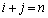 となるところから出てきますが、
となるところから出てきますが、
ただし、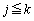 なので、こう書けるためには、
なので、こう書けるためには、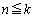 でなければいけません。
でなければいけません。
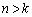 になってしまうと、“
になってしまうと、“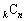 ”と書けなくなります。
”と書けなくなります。
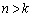 のときには、
のときには、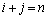 となるためには、
となるためには、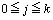 を満たす
を満たす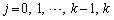 に対応して、
に対応して、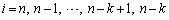 となります(
となります(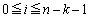 の部分は出てきません)。このときの
の部分は出てきません)。このときの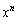 の係数は、
の係数は、
従って、題意を証明するためには、kをある与えられた正整数だとして、
・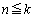 の場合には、
の場合には、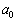 ,
,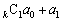 ,
,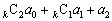 ,・・・,
,・・・,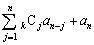 がすべて整数であるとき、
がすべて整数であるとき、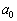 ,
,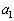 ,
,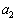 ,・・・,
,・・・,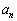 もすべて整数であること、
もすべて整数であること、 ・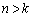 の場合には、
の場合には、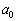 ,
,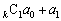 ,
,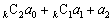 ,・・・,
,・・・,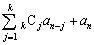 がすべて整数であるとき、
がすべて整数であるとき、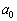 ,
,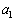 ,
,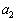 ,・・・,
,・・・,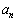 もすべて整数であること
もすべて整数であること を示せばよいことになります。
・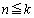 の場合には、
の場合には、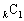 ,・・・,
,・・・,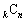
・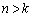 の場合には、
の場合には、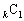 ,・・・,
,・・・,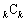
は、すべて整数です。
従って、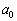 ,
,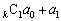 が整数であれば、
が整数であれば、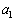 も整数です。
も整数です。
が整数であれば、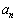 も整数です。
も整数です。
よって、帰納的に、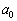 ,
,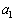 ,
,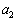 ,・・・,
,・・・,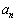 はすべて整数です。 (証明終)
はすべて整数です。 (証明終)
後者の考え方でも、試験会場で充分に実用的ですが、実際にやってみると、予備校講師のようなプロならともかく、答案の形にまとめるのに苦労します。
何となくつかめてはいるのだけれど、あと何をどう整理すればよいのか混乱する、というタイプの問題なのです。
方針転換が道草になる、ということもあるのですが、この問題では、10分から15分くらいで、前者の考え方に方針転換すれば、10分かからないで答案をまとめることができると思います。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。