東大文系数学'08年前期[3]
座標平面上の3点A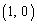 ,B
,B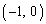 ,C
,C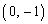 に対し、
に対し、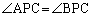 をみたす点Pの軌跡を求めよ。ただし、
をみたす点Pの軌跡を求めよ。ただし、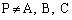 とする。
とする。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 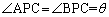 として、ベクトルの内積を用いて、
として、ベクトルの内積を用いて、
としても、計算は猛烈ですが、力尽くでやれば30分あれば解答できると思います(旺文社全国入試問題正解に載っています)。[1],[2]が簡単なので、時間がかかっても腕尽くで計算というのが、この問題では無難だと思います。
ここでは、計算によらないアプローチで考えてみます。
まず、問題文を読んで即浮かぶのは、Pがy 軸上のC以外の点であれば、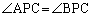 となる(右図黄色線の場合)、ということです。答えがy 軸だけ、というのではあまりに簡単すぎるので、y 軸以外でも、
となる(右図黄色線の場合)、ということです。答えがy 軸だけ、というのではあまりに簡単すぎるので、y 軸以外でも、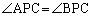 となる場合があるのか、あちこちに点Pをとって調べてみると、点Pが第1象限、あるいは、第2象限にあれば、
となる場合があるのか、あちこちに点Pをとって調べてみると、点Pが第1象限、あるいは、第2象限にあれば、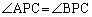 となる場合がありそうです(右図赤線の場合)。
となる場合がありそうです(右図赤線の場合)。
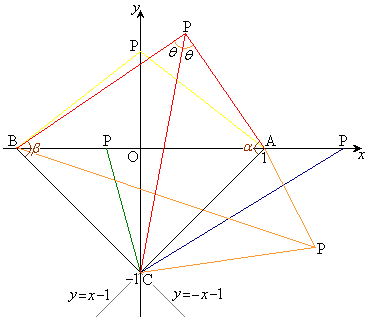 Pが第3象限、第4象限に来る場合はどうか、という前に、x軸上ではどうか、と、調べてみると、線分AB間の原点以外では、
Pが第3象限、第4象限に来る場合はどうか、という前に、x軸上ではどうか、と、調べてみると、線分AB間の原点以外では、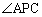 ,
,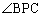 は互いに補角をなす関係にあって、
は互いに補角をなす関係にあって、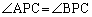 とはなりません(右図緑線の場合)。ですが、x軸上の
とはなりません(右図緑線の場合)。ですが、x軸上の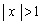 の部分では、APとBPがx軸と重なってしまうので、
の部分では、APとBPがx軸と重なってしまうので、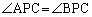 となるのです(右図藍色線の場合)。
となるのです(右図藍色線の場合)。
第3象限の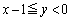 の部分では
の部分では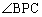 の中に
の中に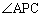 が含まれてしまい、
が含まれてしまい、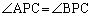 とはなり得ません。第4象限の
とはなり得ません。第4象限の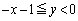 の部分では
の部分では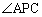 の中に
の中に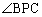 が含まれてしまい、
が含まれてしまい、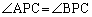 とはなり得ません(右図橙色線の場合)。
とはなり得ません(右図橙色線の場合)。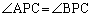 になるとすれば、第3象限の
になるとすれば、第3象限の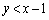 の部分か、第4象限の
の部分か、第4象限の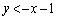 の部分において、ということになります。
の部分において、ということになります。
次に浮かぶことは、△APCと△BPCで何か出てこないか、ということでしょう。
ここで気づくことは、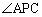 ,
,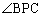 と向かい合っている辺AC,辺BCの長さがともに
と向かい合っている辺AC,辺BCの長さがともに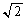 で等しいということです。となれば、正弦定理を使おうということになります。
で等しいということです。となれば、正弦定理を使おうということになります。
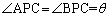 ,
,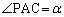 ,
,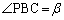 とすると、△APC,△BPCにおいて正弦定理より、
とすると、△APC,△BPCにおいて正弦定理より、
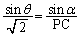 ,
,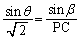
となります。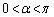 ,
,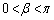 より、
より、
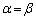 または
または 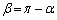
(i) 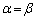 の場合、△APCと△BPCは、2頂角が等しくなるので、
の場合、△APCと△BPCは、2頂角が等しくなるので、 ということは、点Pはy 軸上のC以外の点だということです。
(ii) 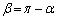 の場合、
の場合、 ・点Pがx軸上にくると、A,B,Pが一直線上に並びます。
点Pが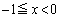 ,
,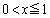 の部分にあるときには、
の部分にあるときには、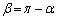 とはなり得ません。
とはなり得ません。
点Pが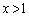 の部分に来ると、
の部分に来ると、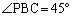 ,
,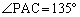 となり、
となり、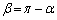 をみたします。
をみたします。
点Pが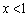 の部分に来ると、
の部分に来ると、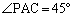 ,
,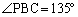 となり、
となり、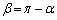 をみたします。
をみたします。
つまり、点Pは、x軸の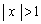 の部分の点です。
の部分の点です。 ・上記で検討したように、点Pが“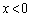 かつ
かつ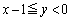 ”の部分、または、“
”の部分、または、“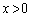 かつ
かつ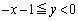 の部分に来ることはありません。
の部分に来ることはありません。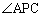 ,
,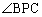 のいずれか一方が他方を含んでしまうので、
のいずれか一方が他方を含んでしまうので、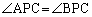 となり得ないからです。
となり得ないからです。 また、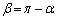 の場合は、
の場合は、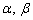 のいずれか一方は
のいずれか一方は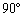 以上の角になりますが、“
以上の角になりますが、“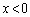 かつ
かつ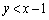 ”,“
”,“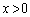 かつ
かつ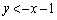 ”の部分に点Pが来てしまうと、
”の部分に点Pが来てしまうと、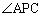 ,
,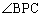 はともに鋭角になってしまう(
はともに鋭角になってしまう( が鈍角になるためには、点Pは
が鈍角になるためには、点Pは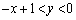 の部分に来なければならない)ので、点Pが第3象限、第4象限に来ることはありません。
の部分に来なければならない)ので、点Pが第3象限、第4象限に来ることはありません。 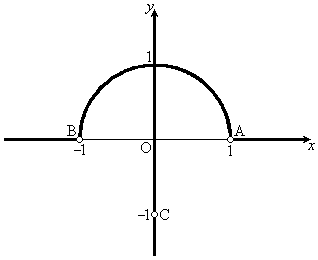 (i),(ii)より、点Pの軌跡は、y 軸上の点Cを除く部分、または、x軸上の
(i),(ii)より、点Pの軌跡は、y 軸上の点Cを除く部分、または、x軸上の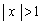 の部分、または、原点を中心とする半径1の円:
の部分、または、原点を中心とする半径1の円: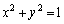 の
の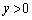 の部分 ......[答]
の部分 ......[答]
図示すると、右図太線のようになります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。