���啶�n���w'08�N�O��[4]
p�����R���Ƃ���B���̊W���Œ�߂��鐔��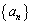 �C
�C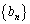 ���l����B
���l����B
(1)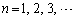 �ɑ��A����2�̐����Ƃ���
�ɑ��A����2�̐����Ƃ���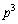 �Ŋ����邱�Ƃ������B
�Ŋ����邱�Ƃ������B 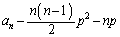 �C
�C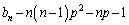
(2) p��3�ȏ�̊�Ƃ���B���̂Ƃ��A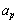 ��
��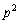 �Ŋ����邪�A
�Ŋ����邪�A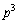 �ł͊����Ȃ����Ƃ������B
�ł͊����Ȃ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�A���Q�����̖��Ɍ����܂����A�����̖��ł��B
�ʓ|�Ȍv�Z���ǂ���肫�邩�A�Ƃ������Ƃł��傤���B
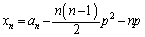 �C
�C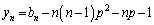
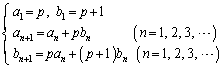 �@����@
�@����@(�T) 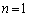 �̂Ƃ��A
�̂Ƃ��A 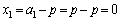 �C
�C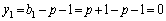
�͂Ƃ���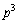 �Ŋ����܂��B
�Ŋ����܂��B (�U) 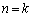 �̂Ƃ��A
�̂Ƃ��A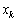 �C
�C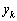 ���Ƃ���
���Ƃ���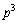 �Ŋ�����A�܂�A
�Ŋ�����A�܂�A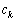 �C
�C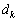 �𐮐��Ƃ��āA
�𐮐��Ƃ��āA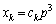 �C
�C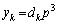 �Ə�����A�ƁA���肵�܂��B
�Ə�����A�ƁA���肵�܂��B 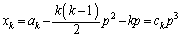 �@����A
�@����A
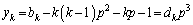 �@����B
�@����B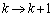 �Ƃ���(
�Ƃ���(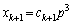 �C
�C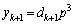 �̌`����邱�Ƃ��ڕW�ł�)�A
�̌`����邱�Ƃ��ڕW�ł�)�A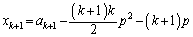 �@����C
�@����C
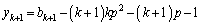 �@����D
�@����D�C�|�A���A
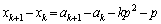 �@����E
�@����E�@�C�B���A
�����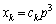 ���A�E�́A
���A�E�́A ���J�b�R���͐����Ȃ̂ŁA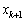 ��
��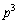 �Ŋ����܂��B
�Ŋ����܂��B
�D�|�B���A 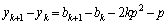 �@����F
�@����F�@���A
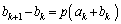 �@����G
�@����G�A�{�B���A
�G�ɑ�����āA
�����̂ł��̒��J�b�R��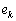 �Ƃ����܂��B
�Ƃ����܂��B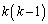 �͘A��2�����̐ςŋ����Ȃ̂�
�͘A��2�����̐ςŋ����Ȃ̂�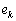 �͐����ł��B
�͐����ł��B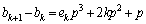 ���F�ɑ�����A
���F�ɑ�����A �B���A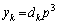 �Ȃ̂ŁA
�Ȃ̂ŁA �J�b�R���͐����Ȃ̂ŁA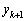 ��
��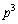 �Ŋ����܂��B
�Ŋ����܂��B
�ȏ���A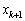 �C
�C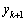 �͂Ƃ���
�͂Ƃ���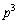 �Ŋ�����̂ŁA
�Ŋ�����̂ŁA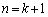 �̂Ƃ����������܂��B
�̂Ƃ����������܂��B (�T)�C(�U)���A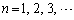 �ɑ��A
�ɑ��A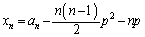 �C
�C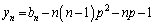 ���Ƃ���
���Ƃ���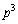 �Ŋ����邱�Ƃ�������܂����B
�Ŋ����邱�Ƃ�������܂����B
(2) (1)���A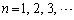 �ɑ��A
�ɑ��A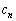 �𐮐��Ƃ��āA
�𐮐��Ƃ��āA �Ƃ������Ƃ��ł��܂��B
�� 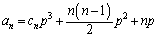
p�͊�Ȃ̂�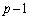 �͋����ł���
�͋����ł���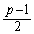 �͐����ł��B
�͐����ł��B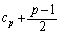 �������ł��B���J�b�R����p�̔{����1�����������̂ɂȂ��Ă��āAp��3�ȏ�̊�̂Ƃ��ɂ�p�Ŋ����܂���B
�������ł��B���J�b�R����p�̔{����1�����������̂ɂȂ��Ă��āAp��3�ȏ�̊�̂Ƃ��ɂ�p�Ŋ����܂���B
����āA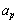 ��
��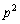 �Ŋ����邪�A
�Ŋ����邪�A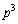 �ł͊����Ȃ����Ƃ�������܂����B
�ł͊����Ȃ����Ƃ�������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 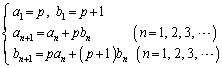
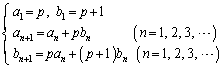 �@����@
�@����@