���啶�n���w'13�N[3]
a�Cb�������̒萔�Ƃ���B����x�Cy��
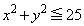 �C
�C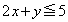
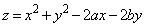 �̍ŏ��l�����߂�B
�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ƃ͌����܂��A�T�d�ȏꍇ�����̍l�@���K�v�Ȗ��ł��B�Ȃ��A���`�v��@���Q�Ƃ��Ă��������B
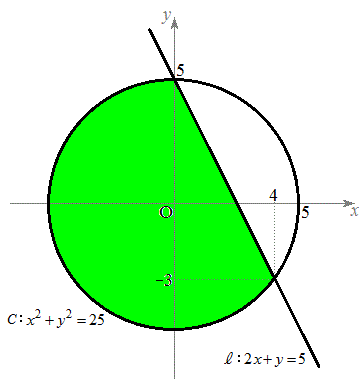
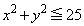 �C
�C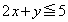
�Ȃ��A �~ C�F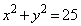 �C����
�C����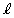 �F
�F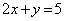 �̌�_�́A������A�����ĉ������Ƃɂ��AA
�̌�_�́A������A�����ĉ������Ƃɂ��AA �CB
�CB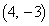 �ł��B
�ł��B
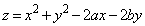 ���A
���A
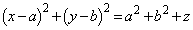 �@����@
�@����@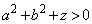 �̂Ƃ��A���a
�̂Ƃ��A���a �C���S
�C���S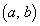 �̉~�ł��B
�̉~�ł��B
 �̂Ƃ��́A
�̂Ƃ��́A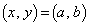 �ƂȂ�A����1�_�ł��Bz�́A����1�ʂ�̒l
�ƂȂ�A����1�_�ł��Bz�́A����1�ʂ�̒l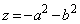 �����Ƃ蓾�Ȃ��̂ŁA���̏ꍇ��z�̍ŏ��l�́A
�����Ƃ蓾�Ȃ��̂ŁA���̏ꍇ��z�̍ŏ��l�́A �ł��B
�ł��B
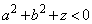 �̂Ƃ��́A�@����
�̂Ƃ��́A�@����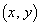 �͑��݂��܂���B
�͑��݂��܂���B
�ȉ��A�~�@�̒��S���A(i)�̈�D�̊O���ɂ���ꍇ�A(ii)�̈�D�̓����ɂ���ꍇ�A�ɕ����čl�@���܂��B
(i) �~�@�̒��S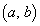 ���A�̈�D�̊O���ɂ���ꍇ
���A�̈�D�̊O���ɂ���ꍇ ���̂Ƃ��́A�~�@���̈�D�Ƌ��L�_�������߂ɏ��Ȃ��Ƃ� (�܂�A
(�܂�A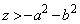 )�ƂȂ�Az���������Ȃ�Ɖ~�@�̔��a���������Ȃ邱�Ƃɒ��ӂ��āA�~�@�Ɨ̈�D�����L�_�����������l���܂��B
)�ƂȂ�Az���������Ȃ�Ɖ~�@�̔��a���������Ȃ邱�Ƃɒ��ӂ��āA�~�@�Ɨ̈�D�����L�_�����������l���܂��B
�~�̔��a���������Ȃ肷����ƁA�̈�D�Ƌ��L�_�������Ȃ��Ȃ�܂��B
�]���āAz���ŏ��ɂȂ�Ƃ��A�~�@�͗̈�D�Ɛڂ��邩�A�̈�D�Ɠ_A�C�_B�݂̂����L����悤�ɂȂ�܂��B
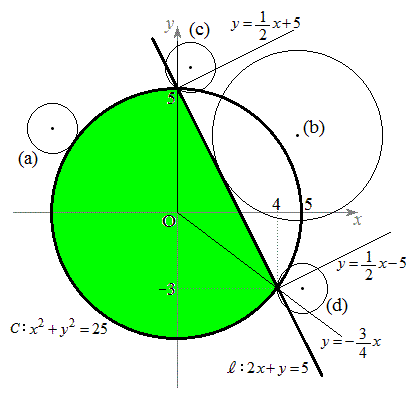 �̈�D�̂ǂ̕����Őڂ��邩�ɂ��A�ꍇ���������܂��B�E�}��(a)�`(d)�̊e��}�����܂��B
�̈�D�̂ǂ̕����Őڂ��邩�ɂ��A�ꍇ���������܂��B�E�}��(a)�`(d)�̊e��}�����܂��B (a) �~�@���A�~C�̗D��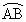 ���1�_P�Őڂ���ꍇ
���1�_P�Őڂ���ꍇ �~�@�̒��S�͉~C�̊O���ɂ���A�~�@�̒��S�Ɖ~C�̒��S�����Ԓ����͐ړ_P��ʂ�܂��B�]���āA���̏ꍇ�AP���D��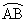 ��Ɉʒu���邽�߂ɂ́A�~�@�̒��S�́A����OA (
��Ɉʒu���邽�߂ɂ́A�~�@�̒��S�́A����OA (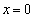 )���獶�����܂��͒���OB (
)���獶�����܂��͒���OB (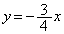 )���牺���̗̈�ɂȂ���Ȃ�܂���B
)���牺���̗̈�ɂȂ���Ȃ�܂���B
�܂�A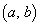 �́A�u
�́A�u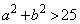 �����h
�����h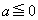 �܂���
�܂���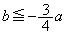 �h�v�����܂��Bz���ŏ��l
�h�v�����܂��Bz���ŏ��l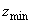 �ɂȂ�Ƃ��A2�~�͊O�ڂ���̂ŁA2�~�̒��S�ԋ�����2�~�̔��a�̘a�Ɉ�v���܂��B����āA
�ɂȂ�Ƃ��A2�~�͊O�ڂ���̂ŁA2�~�̒��S�ԋ�����2�~�̔��a�̘a�Ɉ�v���܂��B����āA �� 
(b) �~�@���A����AB�Ɛڂ���ꍇ
�ړ_��Q�Ƃ��āA�~�@�̒��S��Q�����Ԕ��a�͐���AB�Ɛ����ɂȂ�̂ŁA�~�@�̒��S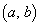 �́A����AB(����
�́A����AB(����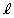 )�̉E��ł����āA����AB(����
)�̉E��ł����āA����AB(���� )��A�Œ������钼��(
)��A�Œ������钼��(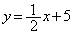 )�ƁA����AB(����
)�ƁA����AB(����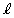 )��B�Œ������钼��(
)��B�Œ������钼��(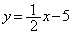 )�ɂ͂��܂ꂽ�̈�ɑ��݂��Ȃ���Ȃ�܂���B
)�ɂ͂��܂ꂽ�̈�ɑ��݂��Ȃ���Ȃ�܂���B
�܂�A �́A�u
�́A�u ����
����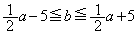 �v�����܂��Bz���ŏ��l
�v�����܂��Bz���ŏ��l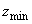 �ɂȂ�Ƃ��A�~�@�̔��a�́A�~�@�̒��S
�ɂȂ�Ƃ��A�~�@�̔��a�́A�~�@�̒��S �ƒ���
�ƒ���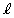 �Ƃ̋����Ɉ�v���܂��B����āA
�Ƃ̋����Ɉ�v���܂��B����āA �� 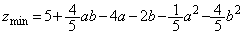
(c) (a)(b)�ȊO�ŁA�~�@���A�̈�D��A�݂̂����L����ꍇ
���̂Ƃ��A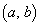 �́A
�́A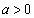 ����
����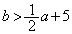 �����܂��Bz���ŏ��l
�����܂��Bz���ŏ��l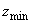 �ɂȂ�Ƃ��A�~�@��A��ʂ�܂��B
�ɂȂ�Ƃ��A�~�@��A��ʂ�܂��B �� 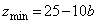
(d) (a)(b)�ȊO�ŁA�~�@���A�̈�D��B�݂̂����L����ꍇ
���̂Ƃ��A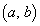 �́A
�́A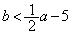 ����
���� �����܂��Bz���ŏ��l
�����܂��Bz���ŏ��l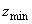 �ɂȂ�Ƃ��A�~�@��B��ʂ�܂��B
�ɂȂ�Ƃ��A�~�@��B��ʂ�܂��B �� 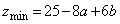
(ii) �~�@�̒��S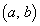 ���A�̈�D�̓����ɂ���ꍇ
���A�̈�D�̓����ɂ���ꍇ ���̂Ƃ��́A�@������1�_ ��\���Ƃ��ɂ��A�̈�D�Ƌ��L�_�����̂ŁA���̂Ƃ�z�͍ŏ��ƂȂ�A
��\���Ƃ��ɂ��A�̈�D�Ƌ��L�_�����̂ŁA���̂Ƃ�z�͍ŏ��ƂȂ�A �ȏ�܂Ƃ߂āAz�̍ŏ��l�́A
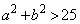 ���u
���u �܂���
�܂���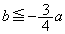 �v�̂Ƃ��A
�v�̂Ƃ��A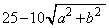
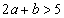 ����
����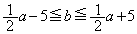 �̂Ƃ��A
�̂Ƃ��A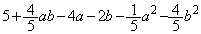
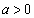 ����
����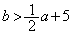 �̂Ƃ��A
�̂Ƃ��A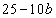
 �̂Ƃ��A
�̂Ƃ��A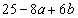
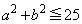 ����
����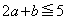 �̂Ƃ��A
�̂Ƃ��A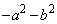 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B