���嗝�n���w'20�N�O��[2]
���ʏ�̓_P�CQ�CR�����꒼����ɂȂ��Ƃ��A������3���_�Ƃ���O�p�`�̖ʐς�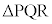 �ŕ\���B�܂��AP�CQ�CR�����꒼����ɂ���Ƃ��́A
�ŕ\���B�܂��AP�CQ�CR�����꒼����ɂ���Ƃ��́A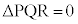 �Ƃ���B
�Ƃ���B
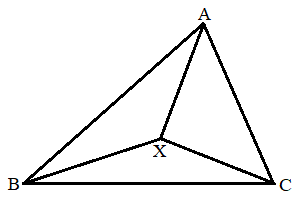
A�CB�CC�ʏ��3�_�Ƃ��A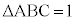 �Ƃ���B���̕��ʏ�̓_X��
�Ƃ���B���̕��ʏ�̓_X��
�����Ȃ��瓮���Ƃ��AX�̓�������͈̖͂ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̂悤�Ɍ����܂����A����Ă݂�ƁA���Z�̓�����肩�A�Ƃ������͋C�ł��B
��蕶�̏����́A
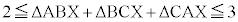 �@���(��)
�@���(��) �܂��AX���O�p�`ABC�̓����A�܂��͎���̓_���Ƃ���(�E�})�ƁA
�܂��AX���O�p�`ABC�̓����A�܂��͎���̓_���Ƃ���(�E�})�ƁA
���̂Ƃ��AX�͏��������܂���BX�͎O�p�`ABC�̊O���̓_�A�Ƃ������ƂɂȂ�܂����A�ʐ�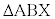 �C
�C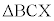 �C
�C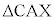 ���l����ƁAX����AB�Ɋւ��ĎO�p�`ABC�Ɣ��Α��AX����BC�Ɋւ��ĎO�p�`ABC�Ɣ��Α��AX����CA�Ɋւ��ĎO�p�`�Ɣ��Α��A�ȂǂŁA�l������ς��Ȃ�������Ȃ��̂ŁA�ꍇ�����̎d���������Ă��܂��B
���l����ƁAX����AB�Ɋւ��ĎO�p�`ABC�Ɣ��Α��AX����BC�Ɋւ��ĎO�p�`ABC�Ɣ��Α��AX����CA�Ɋւ��ĎO�p�`�Ɣ��Α��A�ȂǂŁA�l������ς��Ȃ�������Ȃ��̂ŁA�ꍇ�����̎d���������Ă��܂��B
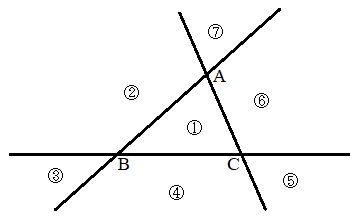 �E�}�̂悤�ɁA�e�ӂ���������3�{�̒����ɂ��A���ʂ�7�̗̈�@�C�A�C�B�C�C�C�D�C�E�C�F�ɕ����܂��B������̓_�͗אڂ���̈�Ɋ܂߂čl���܂��B�O�q�̂悤�ɁAX���̈�@�ɂ���Ƃ��́AX�͏��������܂���B
�E�}�̂悤�ɁA�e�ӂ���������3�{�̒����ɂ��A���ʂ�7�̗̈�@�C�A�C�B�C�C�C�D�C�E�C�F�ɕ����܂��B������̓_�͗אڂ���̈�Ɋ܂߂čl���܂��B�O�q�̂悤�ɁAX���̈�@�ɂ���Ƃ��́AX�͏��������܂���B
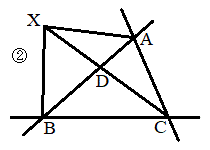 (i) X���̈�A�ɂ���Ƃ�(�E�})�AX���A����BC��A����CA��ɂ���Ƃ����܂߂āA����XC�ƒ���AB�Ƃ̌�_��D (D��A�ƈ�v����Ƃ���
(i) X���̈�A�ɂ���Ƃ�(�E�})�AX���A����BC��A����CA��ɂ���Ƃ����܂߂āA����XC�ƒ���AB�Ƃ̌�_��D (D��A�ƈ�v����Ƃ���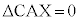 �CD��B�ƈ�v����Ƃ���
�CD��B�ƈ�v����Ƃ���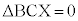 �CD��X�ƈ�v����Ƃ���
�CD��X�ƈ�v����Ƃ���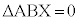 )�Ƃ��܂��B�E�}���A
)�Ƃ��܂��B�E�}���A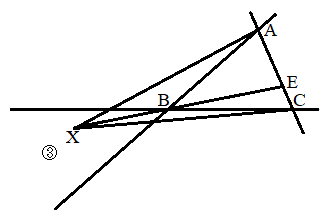 (ii) X���̈�B�ɂ���Ƃ�(�E�})�A����XB�ƕ�CA�Ƃ̌�_��E (E��C���邢��A�ƈ�v���邱�Ƃ�����܂�)�Ƃ��܂��B�E�}���A
(ii) X���̈�B�ɂ���Ƃ�(�E�})�A����XB�ƕ�CA�Ƃ̌�_��E (E��C���邢��A�ƈ�v���邱�Ƃ�����܂�)�Ƃ��܂��B�E�}���A(iii) (i)�C(ii)�Ɠ��l�ɂ��āAX���̈�C�C�̈�D�C�̈�E�C�̈�F�ɂ���Ƃ��́A����CA���C�ɂ���A�Ɣ��Α��ɁA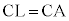 �ƂȂ�悤�ȓ_L���A
�ƂȂ�悤�ȓ_L���A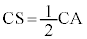 �ƂȂ�悤�ȓ_S���Ƃ�A����BC���C�ɂ���B�Ɣ��Α��ɁA
�ƂȂ�悤�ȓ_S���Ƃ�A����BC���C�ɂ���B�Ɣ��Α��ɁA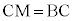 �ƂȂ�悤�ȓ_M���A
�ƂȂ�悤�ȓ_M���A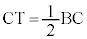 �ƂȂ�悤�ȓ_T���Ƃ�A����AB��ŁAA�ɂ���B�Ɣ��Α��ɁA
�ƂȂ�悤�ȓ_T���Ƃ�A����AB��ŁAA�ɂ���B�Ɣ��Α��ɁA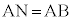 �ƂȂ�悤�ȓ_N���A
�ƂȂ�悤�ȓ_N���A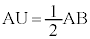 �ƂȂ�悤�ȓ_U���Ƃ�ƁAX�́A��`KLSR�A��`LMTS�A��`MNUT�A��`NIPU�̂��ꂼ��̓����܂��͎���ɂ���܂��B
�ƂȂ�悤�ȓ_U���Ƃ�ƁAX�́A��`KLSR�A��`LMTS�A��`MNUT�A��`NIPU�̂��ꂼ��̓����܂��͎���ɂ���܂��B 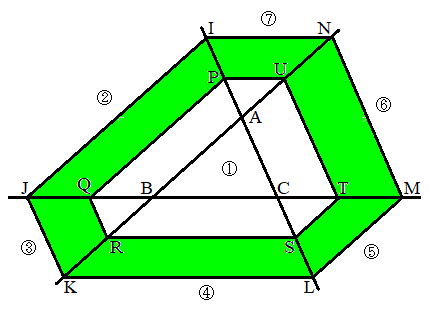 �ȏ��}������ƁAX�͉E�}���ΐF���F���̓����܂��͎���ɂ���A
�ȏ��}������ƁAX�͉E�}���ΐF���F���̓����܂��͎���ɂ���A
X�̓�������͈̖͂ʐς́A��`IJQP�A��`JKRQ�A��`KLSR�A��`LMTS�A��`MNUT�A��`NIPU�����킹�āA
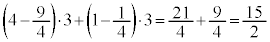 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B