東京大学理系2020年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] a,b,c,pを実数とする。不等式
をすべて満たす実数xの集合と、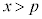 を満たす実数xの集合が一致しているとする。
を満たす実数xの集合が一致しているとする。
(1) a,b,cはすべて0以上であることを示せ。
(2) a,b,cのうち少なくとも1個は0であることを示せ。
(3) 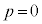 であることを示せ。
であることを示せ。 [解答へ]
[2] 平面上の点P,Q,Rが同一直線上にないとき、それらを3頂点とする三角形の面積を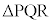 で表す。また、P,Q,Rが同一直線上にあるときは、
で表す。また、P,Q,Rが同一直線上にあるときは、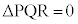 とする。
とする。
A,B,Cを平面上の3点とし、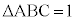 とする。この平面上の点Xが
とする。この平面上の点Xが
を満たしながら動くとき、Xの動きうる範囲の面積を求めよ。
[解答へ]
[3] 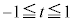 を満たす実数tに対して
を満たす実数tに対して
とする。座標平面上の点P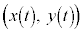 を考える。
を考える。
(1) 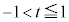 におけるtの関数
におけるtの関数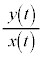 は単調に減少することを示せ。
は単調に減少することを示せ。 (2) 原点とPの距離を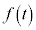 とする。
とする。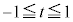 におけるtの関数
におけるtの関数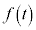 の増減を調べ、最大値を求めよ。
の増減を調べ、最大値を求めよ。 (3) t が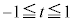 を動くときのPの軌跡をCとし、Cとx軸で囲まれた領域をDとする。原点を中心としてDを時計回りに
を動くときのPの軌跡をCとし、Cとx軸で囲まれた領域をDとする。原点を中心としてDを時計回りに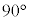 回転させるとき、Dが通過する領域の面積を求めよ。
回転させるとき、Dが通過する領域の面積を求めよ。 [解答へ]
[4] n,kを、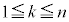 を満たす整数とする。n個の整数
を満たす整数とする。n個の整数
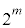 (
(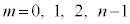 )
)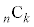 個の積の和を
個の積の和を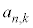 とおく。例えば、
とおく。例えば、
である。
(1) 2以上の整数nに対し、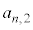 を求めよ。
を求めよ。 (2) 1以上の整数nに対し、xについての整式
を考える。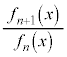 と
と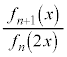 をxについての整式として表せ。
をxについての整式として表せ。 (3) 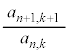 をn,kで表せ。
をn,kで表せ。 [解答へ]
[5] 座標空間において、xy平面上の原点を中心とする半径1の円を考える。この円を底面とし、点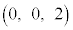 を頂点とする円錐(内部を含む)をSとする。また、点A
を頂点とする円錐(内部を含む)をSとする。また、点A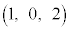 を考える。
を考える。
(1) 点PがSの底面を動くとき、線分APが通過する部分をTとする。平面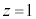 によるSの切り口および、平面
によるSの切り口および、平面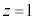 によるTの切り口を同一平面上に図示せよ。
によるTの切り口を同一平面上に図示せよ。 (2) 点PがSを動くとき、線分APが通過する部分の体積を求めよ。
[解答へ]
[6] 以下の問いに答えよ。
(1) A,αを実数とする。θの方程式
を考える。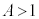 のとき、この方程式は
のとき、この方程式は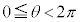 の範囲に少なくとも4個の解を持つことを示せ。
の範囲に少なくとも4個の解を持つことを示せ。 (2) 座標平面上の楕円
C: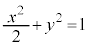
を考える。また、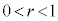 を満たす実数rに対して、不等式
を満たす実数rに対して、不等式 が表す領域をDとする。D内のすべての点Pが以下の条件を満たすような実数r (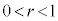 )が存在することを示せ。また、そのようなrの最大値を求めよ。
)が存在することを示せ。また、そのようなrの最大値を求めよ。 条件:C上の点Qで、QにおけるCの接線と直線PQが直交するようなものが少なくとも4個ある。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 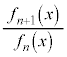 と
と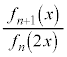 をxについての整式として表せ。
をxについての整式として表せ。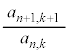 をn,kで表せ。
をn,kで表せ。