���嗝�n���w'20�N�O��[6]
�ȉ��̖₢�ɓ�����B
(1) A�Cα�������Ƃ���Bθ�̕�����
���l����B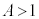 �̂Ƃ��A���̕�������
�̂Ƃ��A���̕�������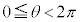 �͈̔͂ɏ��Ȃ��Ƃ�4�̉��������Ƃ������B
�͈̔͂ɏ��Ȃ��Ƃ�4�̉��������Ƃ������B (2) ���W���ʏ�̑ȉ~
C�F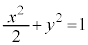
���l����B�܂��A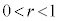 ��������r�ɑ��āA�s����
��������r�ɑ��āA�s���� ���\���̈��D�Ƃ���BD���̂��ׂĂ̓_P���ȉ��̏��������悤�Ȏ���r (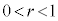 )�����݂��邱�Ƃ������B�܂��A���̂悤��r�̍ő�l�����߂�B
)�����݂��邱�Ƃ������B�܂��A���̂悤��r�̍ő�l�����߂�B �����FC��̓_Q�ŁAQ�ɂ�����C�̐ڐ��ƒ���PQ����������悤�Ȃ��̂����Ȃ��Ƃ�4����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@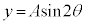 �̃O���t��`���Ă����āA
�̃O���t��`���Ă����āA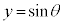 �̃O���t�����낢�땽�s�ړ������A��_�̂ł����ׂ���A�ȉ~��`���āA���낢����ڐ��E�@���������āA�ǂ�����@���������Ə����������A�ȂǁA�������ł����Ԃ������Ē��ׂ�K�v������Ǝv���܂��B�����������ł́A�^�̗ǂ����������Ȃ�e�����Ă��܂��܂��B�����Ă�����Ă��܂��Α債�����ƂłȂ��Ă��A���������{����4�������l����Ƃ��ȂǁA�s���k�o�ʼn^�����ނ��Ƃ���ł��B
�̃O���t�����낢�땽�s�ړ������A��_�̂ł����ׂ���A�ȉ~��`���āA���낢����ڐ��E�@���������āA�ǂ�����@���������Ə����������A�ȂǁA�������ł����Ԃ������Ē��ׂ�K�v������Ǝv���܂��B�����������ł́A�^�̗ǂ����������Ȃ�e�����Ă��܂��܂��B�����Ă�����Ă��܂��Α債�����ƂłȂ��Ă��A���������{����4�������l����Ƃ��ȂǁA�s���k�o�ʼn^�����ނ��Ƃ���ł��B
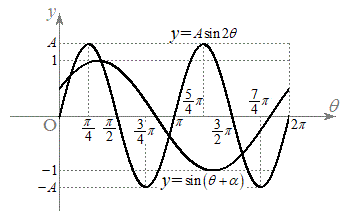
(1) ������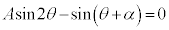 �@(��)
�@(��) �]���āA (��)�́A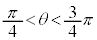 �C
�C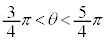 �C
�C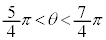 �̊e�͈͂ɏ��Ȃ��Ƃ�1���������܂�(���Ԓl�̒藝���Q��)�B
�̊e�͈͂ɏ��Ȃ��Ƃ�1���������܂�(���Ԓl�̒藝���Q��)�B
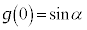 �ɂ��āA
�ɂ��āA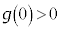 �C
�C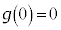 �C
�C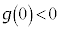 �ɂ��ďꍇ�������܂��B
�ɂ��ďꍇ�������܂��B
�E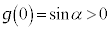 �C�܂�A
�C�܂�A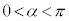 �̂Ƃ��A
�̂Ƃ��A 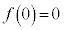 �C
�C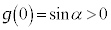 ���A
���A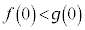
�@���A(��)�́A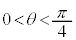 �ɂ����āA���Ȃ��Ƃ�1���������܂��B
�ɂ����āA���Ȃ��Ƃ�1���������܂��B�E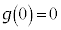 �C�܂�A
�C�܂�A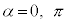 �̂Ƃ��A
�̂Ƃ��A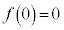 ���A
���A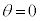 ��(��)�̉��ł��B
��(��)�̉��ł��B
�E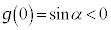 �C�܂�A
�C�܂�A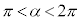 �̂Ƃ��A
�̂Ƃ��A 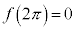 �C
�C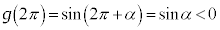 ���A
���A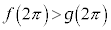
�A���A(��)�́A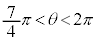 �ɂ����āA���Ȃ��Ƃ�1���������܂��B
�ɂ����āA���Ȃ��Ƃ�1���������܂��B�ȏ���A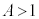 �̂Ƃ��A������(��)�́A
�̂Ƃ��A������(��)�́A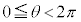 �͈̔͂ɏ��Ȃ��Ƃ�4�̉��������܂��B
�͈̔͂ɏ��Ȃ��Ƃ�4�̉��������܂��B �NjL�D����ŁA(1)�͎����Ă���킯�ł����A�����ŁA�@�𗘂����āA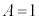 ��������ǂ��Ȃ�̂��A�Ƃ������ƂׂĂ݂܂��B
��������ǂ��Ȃ�̂��A�Ƃ������ƂׂĂ݂܂��B
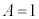 �̂Ƃ��A
�̂Ƃ��A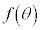 ��
��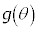 �̐U���͂Ƃ���1�ɂȂ�܂��B
�̐U���͂Ƃ���1�ɂȂ�܂��B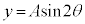 �̃O���t��`���Ă����āA
�̃O���t��`���Ă����āA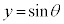 �̃O���t�����낢�땽�s�ړ������Ă����ƁA���������A4��_�����������Ȃ̂ł����A
�̃O���t�����낢�땽�s�ړ������Ă����ƁA���������A4��_�����������Ȃ̂ł����A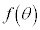 ��
��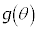 �̎R�̈ʒu���d�Ȃ�����ǂ��������ƂɂȂ�̂��A�Ƃ������ƂɋC�Â��܂��B
�̎R�̈ʒu���d�Ȃ�����ǂ��������ƂɂȂ�̂��A�Ƃ������ƂɋC�Â��܂��B
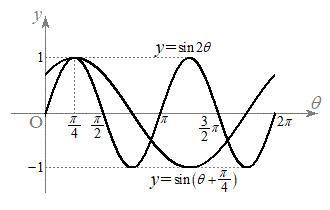 �Ⴆ�A
�Ⴆ�A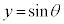 �̃O���t������(
�̃O���t������(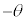 ������)
������)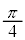 �������s�ړ�������ƁA
�������s�ړ�������ƁA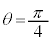 ������ŎR�̈ʒu���d�Ȃ�܂��B�����ŁA
������ŎR�̈ʒu���d�Ȃ�܂��B�����ŁA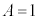 �C
�C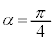 �̏ꍇ�ׂĂ݂܂��B������(��)�́A
�̏ꍇ�ׂĂ݂܂��B������(��)�́A�E�B�́A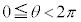 ���A
���A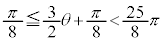 �C���͈̔͂ł́A
�C���͈̔͂ł́A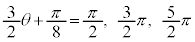 �@��
�@�� 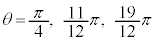
�E�C�́A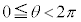 ���A
���A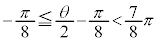 �C���͈̔͂ł́A
�C���͈̔͂ł́A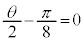 �@��
�@�� 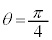
���̂Ƃ��́A������(��)�́A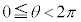 �͈̔͂�3��
�͈̔͂�3��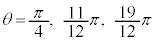 ���������܂���B
���������܂���B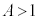 �łȂ���A������(��)���K��4�������Ƃ͌����Ȃ��̂ł��B
�łȂ���A������(��)���K��4�������Ƃ͌����Ȃ��̂ł��B
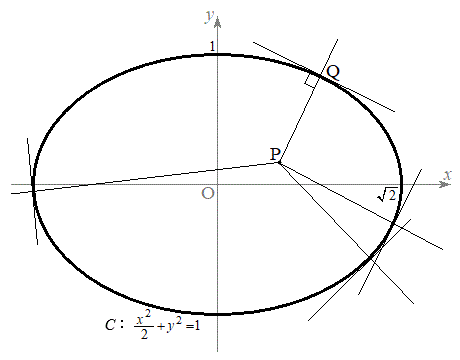 (2) �ȉ~C�F
(2) �ȉ~C�F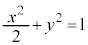 ��̓_Q
��̓_Q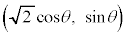 �ɂ�����C�̐ڐ��́A
�ɂ�����C�̐ڐ��́A����������Ȓ����́Ax�Cy�̌W�����Ђ�����Ԃ��āA�Е��Ƀ}�C�i�X�����邱�Ƃɂ��A 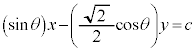 �@(c�F�萔)�@����D
�@(c�F�萔)�@����D���ꂪQ��ʂ邱�Ƃ���A
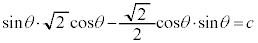 �C�܂�A
�C�܂�A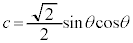
����āA�D�́A
�s����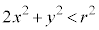 �Ƃ�������������A
�Ƃ�������������A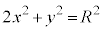 �Ƃ����āA �E���ȉ~
�Ƃ����āA �E���ȉ~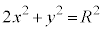 ��̓_
��̓_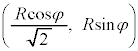 ��ʂ�Ƃ��āA
��ʂ�Ƃ��āA θ�̕������F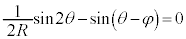 �@����F�@���A���Ȃ��Ƃ�4�̉������̂́A(1)���A
�@����F�@���A���Ȃ��Ƃ�4�̉������̂́A(1)���A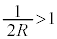 �C���Ȃ킿�A
�C���Ȃ킿�A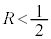 �̂Ƃ��ł��B
�̂Ƃ��ł��B
�܂�A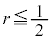 �ƂȂ�悤��r���Ƃ�A
�ƂȂ�悤��r���Ƃ�A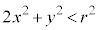 �ƂȂ�S�Ă̓_P�ɂ��āA����C�͖�������A����C����r�͑��݂��܂��B
�ƂȂ�S�Ă̓_P�ɂ��āA����C�͖�������A����C����r�͑��݂��܂��B
�܂��A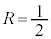 �̂Ƃ��ɂ́A(1)�̒NjL�ŏq�ׂ��悤�ɁA
�̂Ƃ��ɂ́A(1)�̒NjL�ŏq�ׂ��悤�ɁA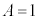 �ƂȂ��āA�F��4�������Ȃ��ꍇ������̂ŁA4�������߂ɂ�
�ƂȂ��āA�F��4�������Ȃ��ꍇ������̂ŁA4�������߂ɂ�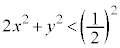 �ł��邱�Ƃ��K�v�ŁAr�̍ő�l��
�ł��邱�Ƃ��K�v�ŁAr�̍ő�l�� ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 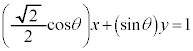
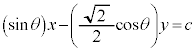 �@(c�F�萔)�@����D
�@(c�F�萔)�@����D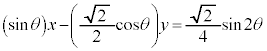 �C���ӂ�
�C���ӂ�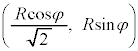 ��ʂ�Ƃ��āA
��ʂ�Ƃ��āA