���嗝�n���w'20�N�O��[1]
a�Cb�Cc�Cp�������Ƃ���B�s����
�����ׂĖ���������x�̏W���ƁA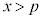 ��������x�̏W������v���Ă���Ƃ���B
��������x�̏W������v���Ă���Ƃ���B
(1) a�Cb�Cc�͂��ׂ�0�ȏ�ł��邱�Ƃ������B
(2) a�Cb�Cc�̂������Ȃ��Ƃ�1��0�ł��邱�Ƃ������B
(3) 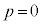 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�ɁA�u���ׂ�0�ȏ�v�A�u���Ȃ��Ƃ�1�v�Ƃ����悤�Ȍ��t���o�Ă���̂ŁA�w���@�ŏؖ����܂�(�ؖ��̋Z�I���Q��)�B�������₷�����邽�߂��W����p���āA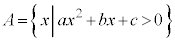 �C
�C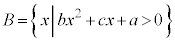 �C
�C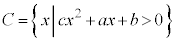 �C
�C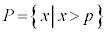 �C
�C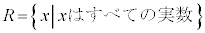 �Ƃ��܂��B�܂��A������
�Ƃ��܂��B�܂��A������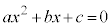 �̔��ʎ��F
�̔��ʎ��F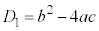 �C����
�C����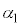 �C
�C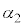 (�Ƃ��Ɏ����̂Ƃ��ɂ�
(�Ƃ��Ɏ����̂Ƃ��ɂ�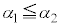 �Ƃ���)�C������
�Ƃ���)�C������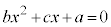 �̔��ʎ��F
�̔��ʎ��F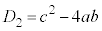 �C����
�C����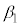 �C
�C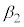 (�Ƃ��Ɏ����̂Ƃ��ɂ�
(�Ƃ��Ɏ����̂Ƃ��ɂ�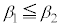 �Ƃ���)�C������
�Ƃ���)�C������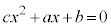 �̔��ʎ��F
�̔��ʎ��F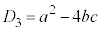 �C����
�C����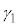 �C
�C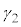 (�Ƃ��Ɏ����̂Ƃ��ɂ�
(�Ƃ��Ɏ����̂Ƃ��ɂ�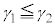 �Ƃ���)�Ƃ��܂��B
�Ƃ���)�Ƃ��܂��B
�����F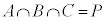 ��(��)�Ƃ��܂��B
��(��)�Ƃ��܂��B
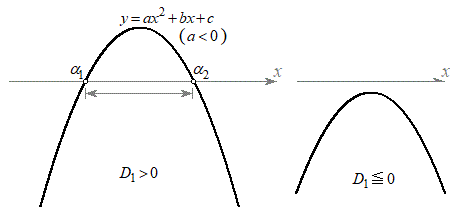 (1) a�Cb�Cc�̂����ǂꂩ��A�Ⴆ��a (b�Cc�ł����l�ł�)��
(1) a�Cb�Cc�̂����ǂꂩ��A�Ⴆ��a (b�Cc�ł����l�ł�)��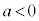 ���Ɖ��肵�܂�(
���Ɖ��肵�܂�(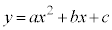 �̃O���t�͉E�}�̂悤�ȏ�ɓʂȕ������B2���������̈�ʘ_���Q��)�B
�̃O���t�͉E�}�̂悤�ȏ�ɓʂȕ������B2���������̈�ʘ_���Q��)�B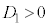 �̂Ƃ��A
�̂Ƃ��A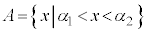
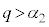 ����
����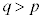 �ƂȂ�q�ɂ��āA
�ƂȂ�q�ɂ��āA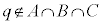 �C
�C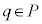 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA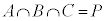 �Ƃ͂Ȃ蓾���A(��)�͐������܂���B
�Ƃ͂Ȃ蓾���A(��)�͐������܂���B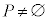 �Ȃ̂ŁA
�Ȃ̂ŁA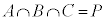 �Ƃ͂Ȃ蓾���A(��)�͐������܂���B
�Ƃ͂Ȃ蓾���A(��)�͐������܂���B�ȏ���Aa�Cb�Cc�̂����ǂꂩ��������Ɖ��肷���(��)�����������A����͌��ŁAa�Cb�Cc�͂��ׂ�0�ȏ�ł��B
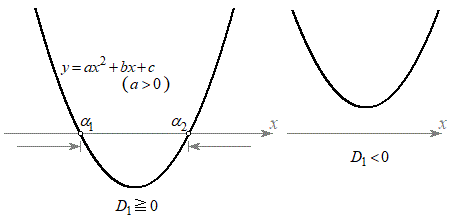 (2) (1)���l�����āAa�Cb�Cc�����ׂĐ����Ɖ��肵�܂�(
(2) (1)���l�����āAa�Cb�Cc�����ׂĐ����Ɖ��肵�܂�(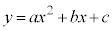 �̃O���t�͉E�}�̂悤�ȉ��ɓʂȕ������B2���������̈�ʘ_���Q��)�B
�̃O���t�͉E�}�̂悤�ȉ��ɓʂȕ������B2���������̈�ʘ_���Q��)�B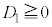 �̂Ƃ��A
�̂Ƃ��A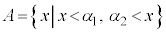 �@����@
�@����@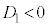 �̂Ƃ��A
�̂Ƃ��A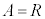 �@����A
�@����A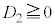 �̂Ƃ��A
�̂Ƃ��A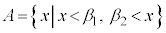 �@����B
�@����B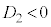 �̂Ƃ��A
�̂Ƃ��A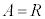 �@����C
�@����C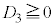 �̂Ƃ��A
�̂Ƃ��A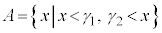 �@����D
�@����D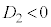 �̂Ƃ��A
�̂Ƃ��A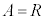 �@����E
�@����E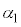 �C
�C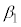 �C
�C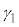 �̒��Ɏ����������(�@�܂��͇B�܂��͇D�̂Ƃ�)�A���̂ǂ�����������A���A
�̒��Ɏ����������(�@�܂��͇B�܂��͇D�̂Ƃ�)�A���̂ǂ�����������A���A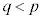 �ƂȂ�q�C
�ƂȂ�q�C
���邢�́A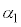 �C
�C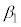 �C
�C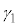 �̒��Ɏ������Ȃ����(�A���C���E�̂Ƃ�)�A
�̒��Ɏ������Ȃ����(�A���C���E�̂Ƃ�)�A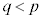 �ƂȂ�q�C
�ƂȂ�q�C
�ɂ��āA
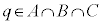 �C
�C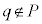 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA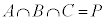 �Ƃ͂Ȃ蓾���A(��)�͐������܂���B
�Ƃ͂Ȃ蓾���A(��)�͐������܂���B
����āAa�Cb�Cc�����ׂĐ����Ɖ��肷���(��)�����������A����͌��ŁA(1)���l�����āAa�Cb�Cc�̂������Ȃ��Ƃ�1��0�ł��B
(3) (2)���Aa�Cb�Cc�̂������Ȃ��Ƃ�1��0�Ȃ̂ŁA�Ⴆ��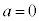 (
(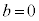 �̏ꍇ�A
�̏ꍇ�A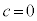 �̏ꍇ�����l�ł�)�Ƃ��܂��B
�̏ꍇ�����l�ł�)�Ƃ��܂��B (i) 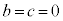 �̂Ƃ��A
�̂Ƃ��A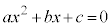 �Ȃǂ���蕶�̕s������
�Ȃǂ���蕶�̕s������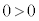 �ƂȂ�܂����A�����͐��藧���Ȃ��̂ŁA
�ƂȂ�܂����A�����͐��藧���Ȃ��̂ŁA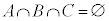 �ƂȂ�A
�ƂȂ�A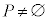 �Ȃ̂ŁA
�Ȃ̂ŁA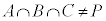 �ŁA(��)�͐������܂���B
�ŁA(��)�͐������܂���B 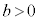 ����
����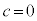 �����l�ł��B
�����l�ł��B����āA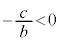 ���A
���A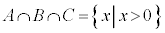
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B