���嗝�n���w'20�N�O��[4]
n�Ck���A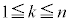 ���������Ƃ���Bn�̐���
���������Ƃ���Bn�̐���
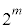 (
(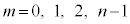 )
)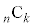 �̐ς̘a��
�̐ς̘a��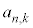 �Ƃ����B�Ⴆ�A
�Ƃ����B�Ⴆ�A
�ł���B
(1) 2�ȏ�̐���n�ɑ��A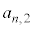 �����߂�B
�����߂�B (2) 1�ȏ�̐���n�ɑ��Ax�ɂ��Ă̐���
���l����B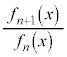 ��
��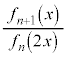 ��x�ɂ��Ă̐����Ƃ��ĕ\���B
��x�ɂ��Ă̐����Ƃ��ĕ\���B (3) 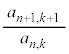 ��n�Ck�ŕ\���B
��n�Ck�ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��͂�����Ȃ�A��蕶�����������ŁA��{�Ώ̎��A�Ⴆ�A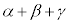 (3��������1������I��Řa�����)�C
(3��������1������I��Řa�����)�C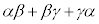 (3��������2������I��ō�����ς̘a)�C
(3��������2������I��ō�����ς̘a)�C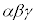 (3��������3������I��ō������)�̂ł������v���o���邩���m��܂��A��ʂ̎��ł́A�����Ȃ肱�̖����������Ă��A�����������A�ǂ�������t����悢�������킩��Ȃ������m��܂���B���������Ƃ��́An�Ck�ɐ��l�������āA���o�����ނƂ��납��n�߂܂��B
(3��������3������I��ō������)�̂ł������v���o���邩���m��܂��A��ʂ̎��ł́A�����Ȃ肱�̖����������Ă��A�����������A�ǂ�������t����悢�������킩��Ȃ������m��܂���B���������Ƃ��́An�Ck�ɐ��l�������āA���o�����ނƂ��납��n�߂܂��B
�܂��A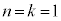 �̂Ƃ��A1�̐����A
�̂Ƃ��A1�̐����A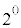 ����قȂ�1��I��Őς����ƁA
����قȂ�1��I��Őς����ƁA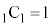 �̐ς̘a
�̐ς̘a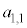 �́A
�́A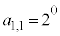 �ƂȂ�܂��B��ŁA���ʂ����悭���邽�߂ɁA
�ƂȂ�܂��B��ŁA���ʂ����悭���邽�߂ɁA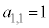 �Ə����Ȃ��ŁA��蕶�̗�̒ʂ�A
�Ə����Ȃ��ŁA��蕶�̗�̒ʂ�A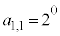 �Ə����悤�ɂ��܂��B��蕶���q���g�ɂȂ��Ă���̂ł��B
�Ə����悤�ɂ��܂��B��蕶���q���g�ɂȂ��Ă���̂ł��B
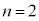 �̂Ƃ��A
�̂Ƃ��A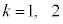 ��2�ʂ�̉\��������܂��B2�̐����́A
��2�ʂ�̉\��������܂��B2�̐����́A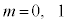 �Ƃ��āA
�Ƃ��āA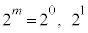 �ł��B
�ł��B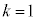 �̂Ƃ��́A2����1��I��Őς����ƁA
�̂Ƃ��́A2����1��I��Őς����ƁA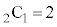 �̐ς̘a
�̐ς̘a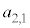 �́A
�́A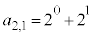 (
(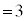 )�ƂȂ�܂��B
)�ƂȂ�܂��B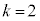 �̂Ƃ��́A2����2��I��Őς����ƁA
�̂Ƃ��́A2����2��I��Őς����ƁA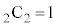 �̐ς̘a
�̐ς̘a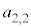 �́A
�́A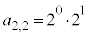 (
(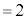 )�ƂȂ�܂�(�g�ݍ��킹���Q��)�B
)�ƂȂ�܂�(�g�ݍ��킹���Q��)�B
 �̂Ƃ��Ak = 1�C2�C3��3�ʂ�̉\��������܂��B3�̐����́A
�̂Ƃ��Ak = 1�C2�C3��3�ʂ�̉\��������܂��B3�̐����́A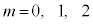 �Ƃ��āA
�Ƃ��āA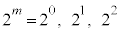 �ł��B
�ł��B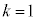 �̂Ƃ��A3����1��I��Őς����Ɛς̘a�́A
�̂Ƃ��A3����1��I��Őς����Ɛς̘a�́A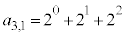 (
(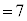 )
)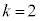 �̂Ƃ��A3����2��I��Őς����Ɛς̘a�́A
�̂Ƃ��A3����2��I��Őς����Ɛς̘a�́A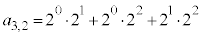 (
(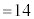 )
)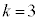 �̂Ƃ��A3����3��I��Őς����Ɛς̘a�́A
�̂Ƃ��A3����3��I��Őς����Ɛς̘a�́A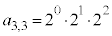 (
(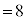 )
)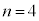 �̂Ƃ��A4�̐����́A
�̂Ƃ��A4�̐����́A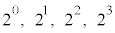 �ł��B
�ł��B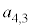 �͖�蕶�ɏo�Ă��܂����A
�͖�蕶�ɏo�Ă��܂����A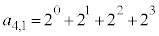 (
(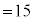 )�C
)�C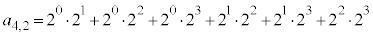 (
(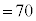 )�C
)�C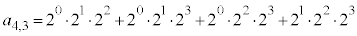 (
(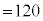 )�C
)�C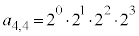 (
(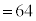 )
)
(1) ��L�ŁA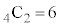 �̐ς̘a
�̐ς̘a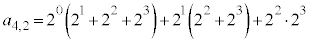 ����l������A
����l������A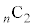 �̐ς̘a
�̐ς̘a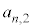 �́A
�́A
(2) 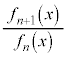 �C
�C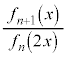 ��x�̐����ŕ\�����A�Ƃ������Ƃ́A
��x�̐����ŕ\�����A�Ƃ������Ƃ́A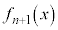 �́A
�́A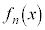 �ł��A
�ł��A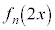 �ł�������A�Ƃ������Ƃł��B
�ł�������A�Ƃ������Ƃł��B �ƁA���������ł���̂ŁA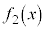 ��
��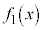 �Ŋ����āA
�Ŋ����āA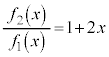
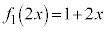 ���A
���A�ƁA���������ł���̂ŁA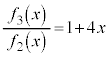 �C
�C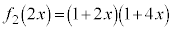 ���A
���A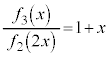
����ŁA���̔w�i�������Ă��܂��B
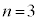 �̏ꍇ�A
�̏ꍇ�A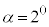 �C
�C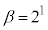 �C
�C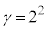 �Ƃ��āA
�Ƃ��āA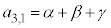 �C
�C �C
�C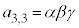 �ƂȂ�̂ŁA��ʂ�n�̏ꍇ�A
�ƂȂ�̂ŁA��ʂ�n�̏ꍇ�A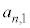 �C
�C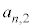 �C����C
�C����C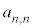 ��n�����ɂ��Ă̊�{�Ώ̎�������Ă���킯�ł��B
��n�����ɂ��Ă̊�{�Ώ̎�������Ă���킯�ł��B �ƂȂ�̂ŁA
�̂悤�ɂȂ��Ă���̂��낤�Ǝ@�m�ł��܂��B�ŏ�����C�Â���A�{��͂Ђ��������������̌v�Z���ł����A�������ŁA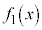 �C
�C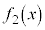 �C
�C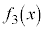 �ƒ��ׂ邤���ɋC�Â��A�Ƃ����̂ŏ[���ɊԂɍ����܂��B
�ƒ��ׂ邤���ɋC�Â��A�Ƃ����̂ŏ[���ɊԂɍ����܂��B
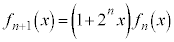 ���ؖ����܂��B
���ؖ����܂��B 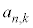 (
(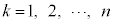 )�́An�̐���
)�́An�̐���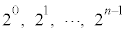 ����قȂ�k��I��Őς��Ƃ�Ak�̐����̑I�ѕ����ׂĂɑ��č������(
����قȂ�k��I��Őς��Ƃ�Ak�̐����̑I�ѕ����ׂĂɑ��č������(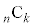 ����)�̘a�ł��B�܂�A
����)�̘a�ł��B�܂�A������
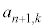 (
(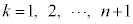 )�́A
)�́A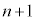 �̐���
�̐���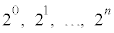 ����قȂ�k��I��Őς��Ƃ�Ak�̐����̑I�ѕ����ׂĂɑ��ĂƂ�����(
����قȂ�k��I��Őς��Ƃ�Ak�̐����̑I�ѕ����ׂĂɑ��ĂƂ�����(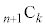 ����)�̘a�ł��B���āA
����)�̘a�ł��B���āA �@����@
�@����@�܂��Ax�̌W���́A
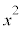 �̌W���́A
�̌W���́A�܂�An�̐���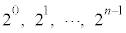 ����قȂ�k��I��Őς����Ak�̐����̑I�ѕ����ׂĂɑ��č������(
����قȂ�k��I��Őς����Ak�̐����̑I�ѕ����ׂĂɑ��č������(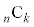 ����)�̘a�A
����)�̘a�A
�ƁAn�̐���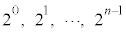 �����قȂ�
�����قȂ�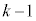 ��I��Őς��Ƃ�A
��I��Őς��Ƃ�A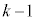 �̐����̑I�ѕ����ׂĂɑ��č������(
�̐����̑I�ѕ����ׂĂɑ��č������(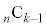 ����)�̊e�X��
����)�̊e�X��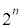 ���������̂���
���������̂���
�Ƃ̘a�ɂȂ��Ă��āA���ǁA
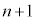 �̐���
�̐���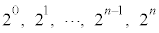 ����قȂ�k��I��Őς��Ƃ�Ak�̐����̑I�ѕ����ׂĂɑ��č������(
����قȂ�k��I��Őς��Ƃ�Ak�̐����̑I�ѕ����ׂĂɑ��č������(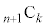 ����A
����A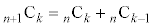 �ɒ���)�̘a
�ɒ���)�̘a
�ɂȂ��Ă���̂ŁA 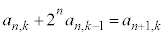 �@����A
�@����A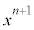 �̌W���́A
�̌W���́A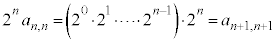
������A�@�́A�]���āA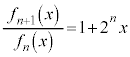 ......[��]�@����B
......[��]�@����B 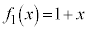 �C�B���J��Ԃ��ėp���邱�Ƃɂ��A
�C�B���J��Ԃ��ėp���邱�Ƃɂ��A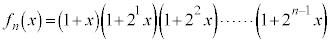
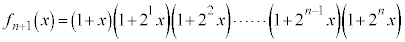 �C
�C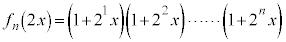
����āA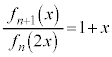 ......[��]�@����C
......[��]�@����C ���D��L�̂悤��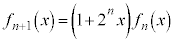 ���ؖ����v�Z���Ď����̂ł́A���Ԃ��������ɁA���ėp���ɏ�������Ȃ��Ȃ�܂��B����I�ɂ́A�A�̐����������āA�B�C�C�����x�őË�����ׂ��ł��B���邢�́A
���ؖ����v�Z���Ď����̂ł́A���Ԃ��������ɁA���ėp���ɏ�������Ȃ��Ȃ�܂��B����I�ɂ́A�A�̐����������āA�B�C�C�����x�őË�����ׂ��ł��B���邢�́A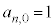 �Ƃ��āA
�Ƃ��āA �ƈ��������ł���A�ƁA�ŏ�����f�肵�ē��Ă������n�߂�̂������ł��B
(3) �C���A
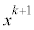 �̌W��(�㎮�̓�d��)�́A
�̌W��(�㎮�̓�d��)�́A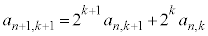 �@����D
�@����D
�A��k��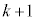 �ɑウ��ƁA
�ɑウ��ƁA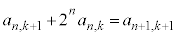 �C����āA
�C����āA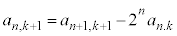 �C�D�ɑ������ƁA
�C�D�ɑ������ƁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 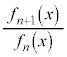 ��
��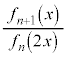 ��x�ɂ��Ă̐����Ƃ��ĕ\���B
��x�ɂ��Ă̐����Ƃ��ĕ\���B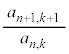 ��n�Ck�ŕ\���B
��n�Ck�ŕ\���B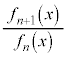 �C
�C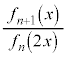 ��x�̐����ŕ\�����A�Ƃ������Ƃ́A
��x�̐����ŕ\�����A�Ƃ������Ƃ́A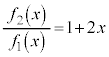
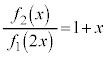
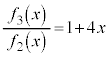 �C
�C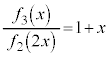
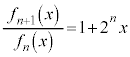 ......[��]�@����B
......[��]�@����B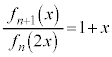 ......[��]�@����C
......[��]�@����C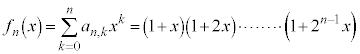
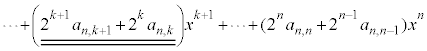
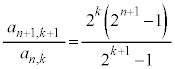 ......[��]
......[��]