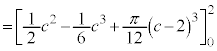���嗝�n���w'20�N�O��[5]
���W��Ԃɂ����āAxy���ʏ�̌��_�𒆐S�Ƃ��锼�a1�̉~���l����B���̉~���ʂƂ��A�_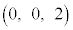 �_�Ƃ���~��(�������܂�)��S�Ƃ���B�܂��A�_A
�_�Ƃ���~��(�������܂�)��S�Ƃ���B�܂��A�_A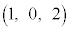 ���l����B
���l����B
(1) �_P��S�̒�ʂ��Ƃ��A����AP���ʉ߂��镔����T�Ƃ���B����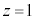 �ɂ��S�̐������сA����
�ɂ��S�̐������сA����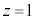 �ɂ��T�̐���ꕽ�ʏ�ɐ}������B
�ɂ��T�̐���ꕽ�ʏ�ɐ}������B (2) �_P��S���Ƃ��A����AP���ʉ߂��镔���̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���~��S���A��ʂ̉~�ɕ��s�ȕ���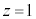 �Ő�Ƃ��́A����͉~�ŁA�~�̔��a�́A�����䂪2�F1�ł��邱�Ƃ���A
�Ő�Ƃ��́A����͉~�ŁA�~�̔��a�́A�����䂪2�F1�ł��邱�Ƃ���A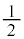 �ɂȂ�܂��B�Ή~���ɂ��Ă��A��ʂ̉~�ɕ��s�ȕ��ʂł̐���͉~�ɂȂ�A�Ƃ������ƂȂǂ�m���Ă���A��������l���ėv�̂悭�ł��܂����A�����ł͂��������m���Ȃ��ōl���Ă݂܂��B
�ɂȂ�܂��B�Ή~���ɂ��Ă��A��ʂ̉~�ɕ��s�ȕ��ʂł̐���͉~�ɂȂ�A�Ƃ������ƂȂǂ�m���Ă���A��������l���ėv�̂悭�ł��܂����A�����ł͂��������m���Ȃ��ōl���Ă݂܂��B
(1) xy���ʏ�ŁA���_�𒆐S�Ƃ��锼�a1�̉~����̓_P�̍��W�́A�}��ϐ�θ��p���āAP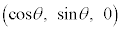 �ƕ\���܂��B�~���̓������l����̂ŁA���̉~����������̓_���l���邱�ƂɂȂ�܂��B
�ƕ\���܂��B�~���̓������l����̂ŁA���̉~����������̓_���l���邱�ƂɂȂ�܂��B ����AP�́A�_A��ʂ�̂ŁA����AP��̓_�̍��W�́A
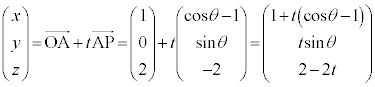 �@(
�@(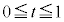 )
)����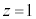 �ɂ�������l����̂ŁA
�ɂ�������l����̂ŁA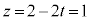 �Ƃ���ƁA
�Ƃ���ƁA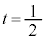 �C����āA
�C����āA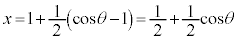 �C
�C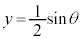
����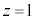 ��̓_��xy���ʂ܂�z���ƕ��s�ɕ��s�ړ������Aθ����������ƁA
��̓_��xy���ʂ܂�z���ƕ��s�ɕ��s�ړ������Aθ����������ƁA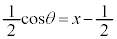 �C
�C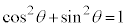 ���A
���A 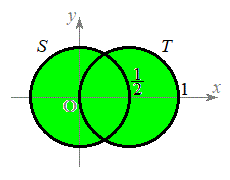 ����́A
����́A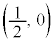 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a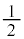 �̉~���ł��BS�̕���
�̉~���ł��BS�̕���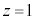 �ɂ�����́A���̉~����������ł����āA���_�𒆐S�Ƃ��锼�a
�ɂ�����́A���̉~����������ł����āA���_�𒆐S�Ƃ��锼�a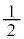 �̉~�ƂȂ�܂��B�~���̓������܂߂�̂ŁA�}������ƁA�E�}���ΐF���F���B
�̉~�ƂȂ�܂��B�~���̓������܂߂�̂ŁA�}������ƁA�E�}���ΐF���F���B
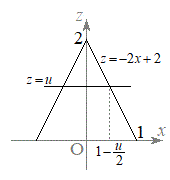 (2) �_P��S���Ƃ��A����AP���ʉ߂��镔����D�Ƃ��܂��B���~��S��zx���ʂŐ�ƁA�E�}�̂悤�Ȓf�ʂ��ł��܂����A
(2) �_P��S���Ƃ��A����AP���ʉ߂��镔����D�Ƃ��܂��B���~��S��zx���ʂŐ�ƁA�E�}�̂悤�Ȓf�ʂ��ł��܂����A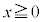 ���ŋ��E�ƂȂ�Ő��̕������́A
���ŋ��E�ƂȂ�Ő��̕������́A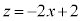 �@����@�@�ł��B
�@����@�@�ł��B���~��S��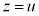 (
(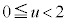 )�Ő�Ɛ���͉~�ɂȂ�܂����A�@��
)�Ő�Ɛ���͉~�ɂȂ�܂����A�@��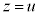 �Ƃ��āA
�Ƃ��āA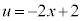 �C
�C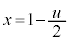 �@����A�C���ꂪ����ɂł���~�̔��a�ɂȂ�܂��B
�@����A�C���ꂪ����ɂł���~�̔��a�ɂȂ�܂��B
���̐���̉~����ɓ_P���Ƃ�ƁA���̍��W��P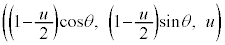 �ƂȂ�܂��BS�͉~���̓������܂߂�̂ŁA���̉~���Ɖ~����������̓_���l���邱�ƂɂȂ�܂��B����AP�̕����x�N�g���́A
�ƂȂ�܂��BS�͉~���̓������܂߂�̂ŁA���̉~���Ɖ~����������̓_���l���邱�ƂɂȂ�܂��B����AP�̕����x�N�g���́A ����AP�́A�_A��ʂ�̂ŁA����AP��̓_�̍��W�́A
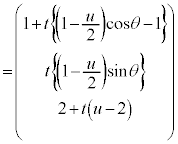 �@(
�@(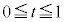 )
)����AP���ʉ߂��镔��D��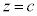 �Ő�ƁA
�Ő�ƁA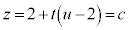 �Ƃ��āA
�Ƃ��āA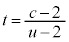
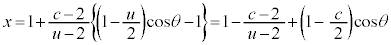 �C
�C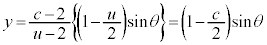
����AP�̒ʉ߂��镔�����l����̂ŁA�ؒf��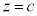 �́A�_P�̑��݂��Ă��镽�ʂ����ɂ���܂��B�܂�A
�́A�_P�̑��݂��Ă��镽�ʂ����ɂ���܂��B�܂�A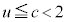 �ł��B
�ł��B
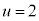 �̏ꍇ�A�܂��́A
�̏ꍇ�A�܂��́A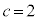 �̏ꍇ�́AD��
�̏ꍇ�́AD��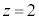 �Ő����f�ʂ́A�����A�������́A1�_A�݂̂ŁA��������f�ʐς�0�ł��B
�Ő����f�ʂ́A�����A�������́A1�_A�݂̂ŁA��������f�ʐς�0�ł��B
����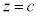 ��̓_��xy���ʂ܂�z���ƕ��s�ɕ��s�ړ�������ƁA����AP�ƕ���
��̓_��xy���ʂ܂�z���ƕ��s�ɕ��s�ړ�������ƁA����AP�ƕ���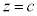 �Ƃ̌�_�́A���S
�Ƃ̌�_�́A���S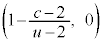 �C���a
�C���a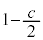 �̉~��`���܂��B���̔��a�́A�_P��z���Wu�ɂ͈ˑ������A�A��蒼�~��S��
�̉~��`���܂��B���̔��a�́A�_P��z���Wu�ɂ͈ˑ������A�A��蒼�~��S��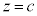 �Ő����Ƃ��̒f�ʂ̉~�̔��a�Ɠ����ł��B�����ł́A�v�Z���Ċm���߂܂������A�����������Ƃ�m���Ƃ��Ď����Ă�����́A��L�̌����͕s�v�ł��B
�Ő����Ƃ��̒f�ʂ̉~�̔��a�Ɠ����ł��B�����ł́A�v�Z���Ċm���߂܂������A�����������Ƃ�m���Ƃ��Ď����Ă�����́A��L�̌����͕s�v�ł��B
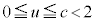 ���A�~�̒��S��x���W
���A�~�̒��S��x���W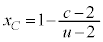 �́Ac���Œ肵�Au�̊��Ƃ݂�0����c�܂�u�����ƁA
�́Ac���Œ肵�Au�̊��Ƃ݂�0����c�܂�u�����ƁA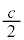 ����0�܂ŒP���Ɍ������܂�(�������̃O���t���Q��)�B
����0�܂ŒP���Ɍ������܂�(�������̃O���t���Q��)�B
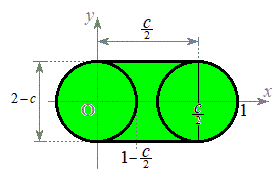
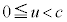 �͈̔͂�u�����Ƃ��A�~�̒��S��
�͈̔͂�u�����Ƃ��A�~�̒��S��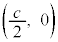 ����
����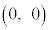 �܂œ����Ȃ���A���a
�܂œ����Ȃ���A���a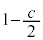 �̉~���������܂߂ē������ƂɂȂ�AD��
�̉~���������܂߂ē������ƂɂȂ�AD��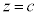 �Ő����Ƃ��̒f�ʂ͉E�}���ΐF���F���ɂȂ�܂��B
�Ő����Ƃ��̒f�ʂ͉E�}���ΐF���F���ɂȂ�܂��B
���̖ʐ�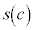 �́A2�ӂ�
�́A2�ӂ�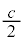 �C
�C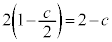 �ł��������`�̖ʐςƁA���a
�ł��������`�̖ʐςƁA���a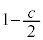 �̉~�̖ʐς̘a�ƂȂ�A
�̉~�̖ʐς̘a�ƂȂ�A 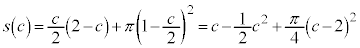 �@(
�@(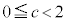 �ł����A���̎���
�ł����A���̎���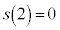 �Ȃ̂ŁA
�Ȃ̂ŁA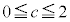 �Ƃ���OK�ł�)
�Ƃ���OK�ł�)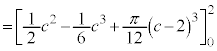
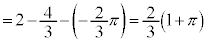 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 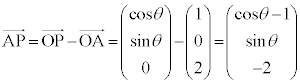
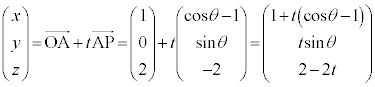 �@(
�@(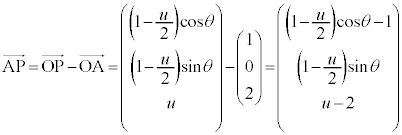
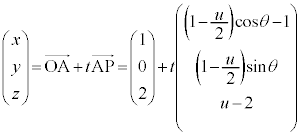
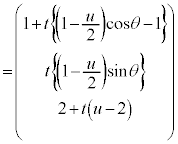 �@(
�@(