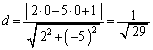���嗝�n���w'91�N�O��[5]
xy���ʏ�Ax���W�Ay���W���Ƃ��ɐ����ł���悤�ȓ_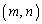 ���i�q�_�ƌĂԁB
���i�q�_�ƌĂԁB
�e�i�q�_�𒆐S�Ƃ��Ĕ��ar�̉~���`����Ă���A�X��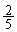 �̔C�ӂ̒����͂����̉~�̂ǂꂩ�Ƌ��L�_�����Ƃ����B���̂悤�Ȑ�����������r�̍ŏ��l�����߂�B
�̔C�ӂ̒����͂����̉~�̂ǂꂩ�Ƌ��L�_�����Ƃ����B���̂悤�Ȑ�����������r�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
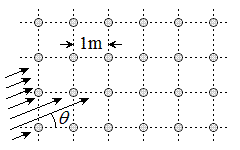 ���@���̈Ӗ��́A�Ԋu1m�̌�Ֆڏ�̈ʒu�ɁA�f�ʂ̉~�̔��a��r�̉~���ƌ��Ȃ���|������ł��āA���̊Ԃ��A�X��
���@���̈Ӗ��́A�Ԋu1m�̌�Ֆڏ�̈ʒu�ɁA�f�ʂ̉~�̔��a��r�̉~���ƌ��Ȃ���|������ł��āA���̊Ԃ��A�X��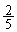 �̕������������˂�����Ƃ��ɁA�������蔲���Ȃ��悤�Ȕ��ar�̍ŏ��l�͂����炩�A�Ƃ������Ƃł��B
�̕������������˂�����Ƃ��ɁA�������蔲���Ȃ��悤�Ȕ��ar�̍ŏ��l�͂����炩�A�Ƃ������Ƃł��B
�|�т̒���������R��Ă���̂����ĘV����������P���������ÓT�ɂ��Ȃ�ŁA�u������P�v���ƁA���͌Ă�ł��܂��B
�i�q�_�́A�܂�ɕ���ł���悤�Ɍ�����̂ł����A���̊Ԃ����蔲���悤�Ƃ���ƈӊO�Ɠ�����̂ł��B�܂��A�����ɂ��蔲���悤�Ƃ����ɁA�����ꂩ�̊i�q�_��ʉ߂��钼������l���邱�Ƃɂ��܂��B
�X��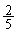 �̒����́A����k��p���āA
�̒����́A����k��p���āA
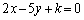 �@����@
�@����@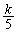 �ł��B
�ł��B
�@���i�q�_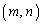 ��ʉ߂���Ƃ��āA
��ʉ߂���Ƃ��āA
�����藧�̂ł����Ak�͂ǂ�Ȑ��ɂȂ�̂ł��傤���H
m�Cn�ɓK���ɐ��������Ă݂܂��B
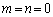 �Ƃ���ƁA
�Ƃ���ƁA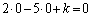 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA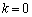 �ł��B
�ł��B
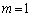 �C
�C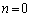 �Ƃ���ƁA
�Ƃ���ƁA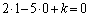 �C
�C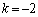
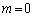 �C
�C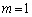 �Ƃ���ƁA
�Ƃ���ƁA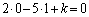 �C
�C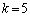
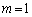 �C
�C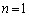 �Ƃ���ƁA
�Ƃ���ƁA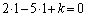 �C
�C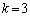
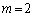 �C
�C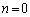 �Ƃ���ƁA
�Ƃ���ƁA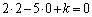 �C
�C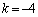
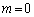 �C
�C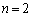 �Ƃ���ƁA
�Ƃ���ƁA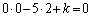 �C
�C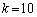
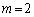 �C
�C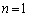 �Ƃ���ƁA
�Ƃ���ƁA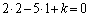 �C
�C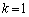
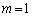 �C
�C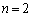 �Ƃ���ƁA
�Ƃ���ƁA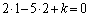 �C
�C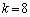
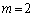 �C
�C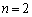 �Ƃ���ƁA
�Ƃ���ƁA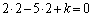 �C
�C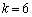
�܂��܂������܂��B
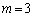 �C
�C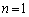 �Ƃ���ƁA
�Ƃ���ƁA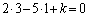 �C
�C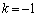
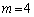 �C
�C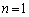 �Ƃ���ƁA
�Ƃ���ƁA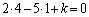 �C
�C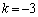
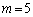 �C
�C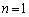 �Ƃ���ƁA
�Ƃ���ƁA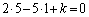 �C
�C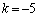
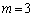 �C
�C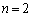 �Ƃ���ƁA
�Ƃ���ƁA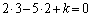 �C
�C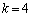
�Ȃ�āA�I�O��Ȃ��Ƃ����ėV��ł���Ɗ����邩���m��܂��A���ꂪ�A���������R�c�Ȃ̂ł���A�܂��A��֑�w�𐧔e���邽�߂̎�@�Ȃ̂ł��B
��L�ŁA�d�v�Ȏ����ɋC������͂��ł��B
k�̒l�Ƃ��ďo�Ă��鐔�́A����C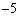 �C
�C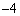 �C
�C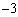 �C
�C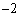 �C
�C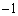 �C0�C1�C2�C3�C4�C5�C6�C�������Ƃ����悤�ɂȂ��Ă��܂��B���[�ȏ����͏o�Ă��܂���B���������ɕ���ł����̂ł��B���ꂪ�A���̖��̃|�C���g�ł��B
�C0�C1�C2�C3�C4�C5�C6�C�������Ƃ����悤�ɂȂ��Ă��܂��B���[�ȏ����͏o�Ă��܂���B���������ɕ���ł����̂ł��B���ꂪ�A���̖��̃|�C���g�ł��B
�܂�A�i�q�_��ʉ߂��钼���@�́A
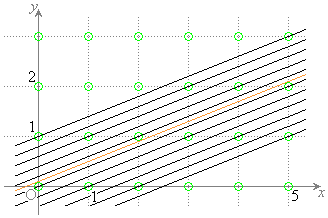 �Ƃ�����ɕ��Ԃ̂ł��B�����xy���ʏ�ɏ����Ă݂�ƉE�}�̂悤�ɓ��Ԋu�ɕ��т܂��B�Ȃ����Ԋu�ɂȂ邩�A�Ƃ����ƁAk�������l���Ƃ邩��ł��Bm�Cn�𐮐��Ƃ��āA
�Ƃ�����ɕ��Ԃ̂ł��B�����xy���ʏ�ɏ����Ă݂�ƉE�}�̂悤�ɓ��Ԋu�ɕ��т܂��B�Ȃ����Ԋu�ɂȂ邩�A�Ƃ����ƁAk�������l���Ƃ邩��ł��Bm�Cn�𐮐��Ƃ��āA
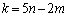
�ƕ\����̂ł�����A�����Ɛ����������Đ����A�������m�����ΐ����Ȃ̂ŁAk�������ɂȂ�͓̂��R�ł��B��L�ł́Ak�����ׂĂ̐������Ƃ肻�����A�Ƃ������Ƃ��m���߂��̂ł��B
�����Ȃ�A�����A�������̂����R�ł��B
��Ղ̖ڏ�ɕ���ł���|���������蔲���čs���̂��Ƃ�����A�E�}�����̒����̂��傤�ǒ���(��F�̒���)��ʂ�悢�̂ł��B
���̖��́A�X��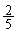 �̒����������̉~�̂ǂꂩ�Ƌ��L�_�����A�ƌ����Ă���̂ł����A����ʉ߂����Ȃ��悤�ȍŏ��̔��a�͂ǂꂾ�����A�Ƃ������Ƃł��B�E�}�̂悤�ɓ��Ԋu�ɕ������̂����A�ׂ荇��2�����̋�����
�̒����������̉~�̂ǂꂩ�Ƌ��L�_�����A�ƌ����Ă���̂ł����A����ʉ߂����Ȃ��悤�ȍŏ��̔��a�͂ǂꂾ�����A�Ƃ������Ƃł��B�E�}�̂悤�ɓ��Ԋu�ɕ������̂����A�ׂ荇��2�����̋�����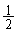 ���ŏ��l�ł��B
���ŏ��l�ł��B
�A�ƇB�̋������l����ƁA�A�͌��_ ��ʂ�̂ŁA���_�ƇB�̋���d���A�_�ƒ����̋����̌������g���ċ��߂�ƁA
��ʂ�̂ŁA���_�ƇB�̋���d���A�_�ƒ����̋����̌������g���ċ��߂�ƁA
���߂�ŏ��l�͂���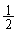 �ŁA
�ŁA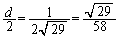 ......[��]
......[��]
����̐��w�̎�����150����6��ł��B1���25�������邱�Ƃ��ł��܂��B��L�̃X�g�[���[�ŏ[����25���ɓ���܂��B���̕�����3�`4����̂ɂ���Ώ[���ɍ��i���C���ɓ���܂��B
��L�ŁA�ǂ����āA�ɂ��ǂ蒅�����̂��A�Ƃ����ƁA�@��x�Cy�ɐ��������Ă݂�����ł��B��֑�w�̖��������A�Ƃ������Ƃ́A���ۓI�ȍ����ȗ��_��U��A�Ƃ������Ƃł͂Ȃ��A�N�ɂł��ȒP�ɂł���V�ѐS�̂悤�ȂƂ��납��A�d�v�Ȏ����ɋC�����A�Ƃ������ƂȂ̂��A�Ƃ������Ƃ����Вm���Ē��������Ǝv���܂��B�`�������W����C������������A�N�ɂł��肪�͂����ƂȂ̂ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B