���勳�琔�w'09�N[4]
���̐���n�ɑ��āA�W�� �̕����W��M�ŏ���
�̕����W��M�ŏ���
 �Ȃ��
�Ȃ��
 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A �̎�肤��ő�l��
�̎�肤��ő�l�� �ƕ\���B
�ƕ\���B
���̖₢�ɓ�����B
(1) n��4�̔{���̂Ƃ��A �����藧���Ƃ������B
�����藧���Ƃ������B (2) n��4�̔{���̂Ƃ��A �����藧���Ƃ������B
�����藧���Ƃ������B (3)  �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�C(2)�͒��ۓI�ōl���Â炢���ł��B�����������́A ���x�Ƃ��ċ�̓I�ɍl����悤�ɂ��܂��B
���x�Ƃ��ċ�̓I�ɍl����悤�ɂ��܂��B
�W�� �̕����W��M�ŏ���
�̕����W��M�ŏ���
 �Ȃ��
�Ȃ�� �@���(��)
�@���(��)
�͏���(��)�����܂��B �ł���
�ł��� �ł��B
�ł��B
���l�ɁA ������(��)�����܂��B
������(��)�����܂��B
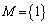 �̂Ƃ��AM��1�̗v�f�����̂ŁA
�̂Ƃ��AM��1�̗v�f�����̂ŁA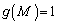 �ł��B
�ł��B
 �͏���(��)�����܂���B
�͏���(��)�����܂���B �̂Ƃ�
�̂Ƃ� �ƂȂ��Ă��܂��܂��B
�ƂȂ��Ă��܂��܂��B
 �͏���(��)�����܂��B
�͏���(��)�����܂��B �Ȃ��
�Ȃ�� �C
�C �Ȃ��
�Ȃ�� �ƂȂ��Ă��܂��B
�ƂȂ��Ă��܂��B �̂Ƃ�
�̂Ƃ� �ł��B
�ł��B
 ������(��)�����܂��B���̂Ƃ�
������(��)�����܂��B���̂Ƃ� �ł��B
�ł��B
�u �̂Ƃ肤��ő�l��
�̂Ƃ肤��ő�l�� �Ƃ���v�Ƃ����̂́A
�Ƃ���v�Ƃ����̂́A �̏ꍇ�A�W��
�̏ꍇ�A�W�� �̕����W�������낢��ƍl���āA����(��)���݂��������W����������Ƃ��ɁA�����Ƃ��v�f���̑傫�Ȃ��̂��l����A�Ƃ������Ƃł��B����(��)���݂��������W��M�̒��ɁA1��2�͓��������A3��6�͓��������A�Ƃ����悤�ɍl���čs���ƁA
�̕����W�������낢��ƍl���āA����(��)���݂��������W����������Ƃ��ɁA�����Ƃ��v�f���̑傫�Ȃ��̂��l����A�Ƃ������Ƃł��B����(��)���݂��������W��M�̒��ɁA1��2�͓��������A3��6�͓��������A�Ƃ����悤�ɍl���čs���ƁA
�̂Ƃ���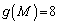 ���ő�v�f���̕����W���ɂȂ�܂��B�ł���A
���ő�v�f���̕����W���ɂȂ�܂��B�ł���A �ł��B
�ł��B �ƂȂ�M�́A���ɂ��A
�ƂȂ�M�́A���ɂ��A �C
�C �Ȃǂ��l�����܂��B
�Ȃǂ��l�����܂��B
�����āA(1)�̖�蕶�́A �Ƃ����s���������藧���Ƃ������A�ƁA�����Ă���킯�ł��B
�Ƃ����s���������藧���Ƃ������A�ƁA�����Ă���킯�ł��B
 �Ƃ����̂́A�W��
�Ƃ����̂́A�W�� �̕����W���̒��ŏ���(��)���݂������̂��l���A�����̒��̍ő�v�f���ł��B1��2�͓����ł��Ȃ��̂ŁA
�̕����W���̒��ŏ���(��)���݂������̂��l���A�����̒��̍ő�v�f���ł��B1��2�͓����ł��Ȃ��̂ŁA �Ƃ������Ƃ͂��蓾�܂���B����(��)�����̂́A
�Ƃ������Ƃ͂��蓾�܂���B����(��)�����̂́A �C
�C �ŁA
�ŁA �ł��B
�ł��B
 �Ȃ̂ŁA
�Ȃ̂ŁA �͖�������Ă��܂��B
�͖�������Ă��܂��B
�܂��A(2)�� ����������Ă��܂��B
����������Ă��܂��B
���āA(1)�ł����A �̂Ƃ��A
�̂Ƃ��A �ƂȂ镔���W��M�̒��ŁA
�ƂȂ镔���W��M�̒��ŁA �ɒ��ڂ��܂��B���̏W���́A
�ɒ��ڂ��܂��B���̏W���́A �̂Ƃ���
�̂Ƃ��� ��^���镔���W��
��^���镔���W�� �ƁA
�ƁA �����v�fx���琬�镔���W��
�����v�fx���琬�镔���W�� �ɕ����邱�Ƃ��ł��܂��B
�ɕ����邱�Ƃ��ł��܂��B �̗v�f����6�Ȃ̂ŁA
�̗v�f����6�Ȃ̂ŁA �Ƃ����s�����́A
�Ƃ����s�����́A
 �̂Ƃ��ɍő�v�f����^���镔���W���́A
�̂Ƃ��ɍő�v�f����^���镔���W���́A �̂Ƃ��ɍő�v�f����^���镔���W���̗v�f�ƁA
�̂Ƃ��ɍő�v�f����^���镔���W���̗v�f�ƁA ����
����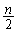 �̗v�f�����ׂĊ܂�ł���B
�̗v�f�����ׂĊ܂�ł���B
��ʂ�n�̏ꍇ�������Ƃ��ɂ́A �ȉ��Ƃ���ȊO�Ƃɕ����Ď������ƂɂȂ�܂��B
�ȉ��Ƃ���ȊO�Ƃɕ����Ď������ƂɂȂ�܂��B
(1)  �Ƃ��܂��B
�Ƃ��܂��B n��4�̔{���̂Ƃ� �͐��̐����ŁA�W��
�͐��̐����ŁA�W�� �́A
�́A �̕����W���ł��B
�̕����W���ł��B
 �̕����W���ł����āA����(��)����
�̕����W���ł����āA����(��)���� (
( �Ƃ���)�ƂȂ�W��
�Ƃ���)�ƂȂ�W�� �̗v�f��m����܂����A��������������ɁA
�̗v�f��m����܂����A��������������ɁA �C
�C �C����C
�C����C �Ƃ��܂��B
�Ƃ��܂��B  �@����@
�@����@�܂��A �C
�C �C����C
�C����C �@����A�@�ł��B
�@����A�@�ł��B
 ����
���� �̗v�fx���琬��W��
�̗v�fx���琬��W�� �́A����(��)�����܂��B�܂�A
�́A����(��)�����܂��B�܂�A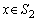 �ł���A
�ł���A �ł��B
�ł��B
�Ȃ��Ȃ�A ���A
���A �@����B�@�ƂȂ邩��ł��B
�@����B�@�ƂȂ邩��ł��B
�����ŁA ���l���܂��B
���l���܂��B
 �C
�C �C����C
�C����C �ɂ��ẮA�@���A
�ɂ��ẮA�@���A �ł����āA�A�����킹�čl����ƁA
�ł����āA�A�����킹�čl����ƁA �C
�C  �C����C
�C����C
�܂��A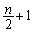 �C
�C �C����Cn�ɂ��ẮA�B���A����2�{��
�C����Cn�ɂ��ẮA�B���A����2�{�� �̗v�f�ł͂���܂���B
�̗v�f�ł͂���܂���B
�]���āA �̂��ׂĂ̗v�f
�̂��ׂĂ̗v�f �ɂ��āA
�ɂ��āA �ł���A
�ł���A ��
�� �̕����W���ŏ���(��)�����܂��B�܂��A
�̕����W���ŏ���(��)�����܂��B�܂��A ���A
���A �ȏ���A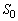 �̕����W��M�ŏ���(��)�������̂ɑ���M�̗v�f�̌���
�̕����W��M�ŏ���(��)�������̂ɑ���M�̗v�f�̌��� �Ƃ���Ƃ��A
�Ƃ���Ƃ��A �̎�肤��ő�l��
�̎�肤��ő�l�� �Ƃ���A
�Ƃ���A
(2) (1)�� �ɑ��A
�ɑ��A ��
�� �̕����W���ŏ���(��)����
�̕����W���ŏ���(��)���� ���Ƃ��܂��B
���Ƃ��܂��B �܂�A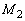 �͏���(��)����
�͏���(��)���� �̕����W���̒��ōő�v�f���̏W��(�K��������ʂ�ł͂���܂���)���Ƃ��܂��B
�̕����W���̒��ōő�v�f���̏W��(�K��������ʂ�ł͂���܂���)���Ƃ��܂��B
 �̗v�f�̒���
�̗v�f�̒��� �ȉ��̗v�f�̌���k�Ƃ���ƁA
�ȉ��̗v�f�̌���k�Ƃ���ƁA �@����C�@�ł��B
�@����C�@�ł��B
������w���@�Ŏ����܂��B���ɁA �̗v�f�̒���
�̗v�f�̒��� �ȉ��̂��̂�
�ȉ��̂��̂� �ȏ゠��Ƃ��āA���̂�����m�ŏW��
�ȏ゠��Ƃ��āA���̂�����m�ŏW�� ��������Ƃ��܂�(
��������Ƃ��܂�( �ɓ���Ȃ��v�f��b�Ƃ��܂�)�B�C�ӂ�
�ɓ���Ȃ��v�f��b�Ƃ��܂�)�B�C�ӂ� �ɂ��āA
�ɂ��āA �ł�����̂�
�ł�����̂� �ł����A�ł���A
�ł����A�ł���A (
( )�ł����āA
)�ł����āA ��(1)�̏W��
��(1)�̏W�� �̕����W���ł����ď���(��)�����̂ŁA
�̕����W���ł����ď���(��)�����̂ŁA �C�܂�A
�C�܂�A �͏���(��)�����ő�v�f���̏W���ł��B�Ƃ��낪�A
�͏���(��)�����ő�v�f���̏W���ł��B�Ƃ��낪�A ����
���� ����
���� �ƂȂ�b�����݂��A
�ƂȂ�b�����݂��A �C�]����
�C�]���� �Ȃ̂ŁA
�Ȃ̂ŁA ��b��t�������Ăł���W����
��b��t�������Ăł���W���� �̕����W���ł����ď���(��)�����Ă��܂��܂��B����́A
�̕����W���ł����ď���(��)�����Ă��܂��܂��B����́A ���ő�v�f���̏W���ł��邱�ƂƖ������܂��B����āA�C�����藧���܂��B
���ő�v�f���̏W���ł��邱�ƂƖ������܂��B����āA�C�����藧���܂��B
 �̗v�f�̒���
�̗v�f�̒��� �ȏ�̗v�f�̌���K�Ƃ���ƁA
�ȏ�̗v�f�̌���K�Ƃ���ƁA �@����D�@�ł��B
�@����D�@�ł��B
�Ȃ��Ȃ�A �́A
�́A �ȏ�n�ȉ��̐����̒��ł́A
�ȏ�n�ȉ��̐����̒��ł́A �����x (�S����
�����x (�S���� ����܂�)�ƁA
����܂�)�ƁA ����y (
����y ( ����܂�)�ɂ��āAy��
����܂�)�ɂ��āAy�� (
( )�̂����ꂩ1��(y��
)�̂����ꂩ1��(y�� ��
�� �̒��œ������܂���)�̌v
�̒��œ������܂���)�̌v �C���킹�āA
�C���킹�āA �ȊO�̗v�f���������Ȃ�����ł��B
�ȊO�̗v�f���������Ȃ�����ł��B
�C�C�D���A
(3) (1)�C(2)���An��4�̔{���̂Ƃ��A
 �ł��B
�ł��B ��4�̔{���Ȃ̂ŁA
��4�̔{���Ȃ̂ŁA������
 �̂Ƃ��A�W��
�̂Ƃ��A�W�� �̕����W���ŁA����(��)�����W���ł����āA�v�f���ő�̂��̂�
�̕����W���ŁA����(��)�����W���ł����āA�v�f���ő�̂��̂� �ŁA
�ŁA �ł��B
�ł��B �́A����
�́A���� �C����4�����䐔����62���̘a�Ƃ��āA
�C����4�����䐔����62���̘a�Ƃ��āA
��  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B