�G�l���M�[�̌����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̂��^���G�l���M�[�̕ω��́A���̊ԂɎ��d���ɓ������B���̌������G�l���M�[�̌����ƌ����B
�^���������F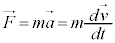 �̗��ӂ������ψ�
�̗��ӂ������ψ�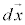 �Ƃ̓��ς��Ƃ�A�ʒu
�Ƃ̓��ς��Ƃ�A�ʒu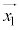 �����ʒu
�����ʒu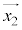 �܂Őϕ����܂��B
�܂Őϕ����܂��B
�@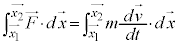 ����@
����@
2�����̉^���̏ꍇ�A���ӂ̐ϕ��́A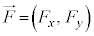 �C
�C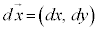 �C
�C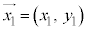 �C
�C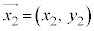 �Ƃ��āA
�Ƃ��āA
�@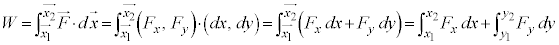 ����A
����A
���̐ϕ��̒l���d���ƌ����B
�E�ӂ̐ϕ��́A
�@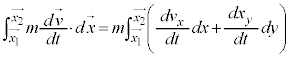 ����B
����B
�����ŁA�E�ӑ�1���̐ϕ���x�̐ϕ�����t�̐ϕ��ɕϊ����܂�(�u���ϕ�)�B ���A
���A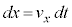 �C
�C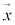 �F
�F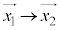 �̂Ƃ��At�F
�̂Ƃ��At�F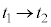 �Ƃ��āA
�Ƃ��āA
�@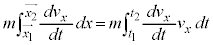
����ɁA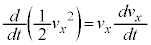 ���At�F
���At�F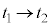 �̂Ƃ��A
�̂Ƃ��A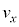 �F
�F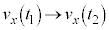 �Ƃ��āA
�Ƃ��āA
�@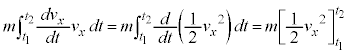
�@�@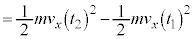
�B�̉E�ӑ�2���̐ϕ������l�ɂ��āAx��y�ɓ���ւ���A
�@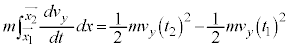
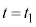 �C
�C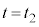 �̂Ƃ������x�����ꂼ��A
�̂Ƃ������x�����ꂼ��A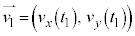 �C
�C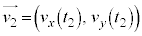 �C�܂��A
�C�܂��A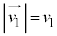 �C
�C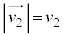 �Ƃ���A�B�́A
�Ƃ���A�B�́A
�@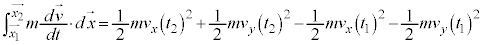
�@�@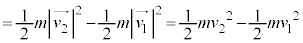 ����C
����C
�@�C�A�C�C���A
�@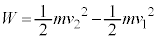
����́A�^���G�l���M�[�̕ω������d���ɓ��������Ƃ������Ă��܂��B
��L�̐����́A���V�̐ϕ����w�K���Ă��Ȃ��l�ɂ͍��x�Ȃ̂ŁA�Ƃ肠�����A�G�l���M�[�̌����̓��e���o���Ă��������B
�d���́A�������ł���ꍇ�ɂ́A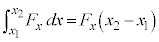 �C
�C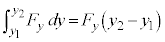 ���A�ψ���
���A�ψ���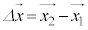 �Ƃ��āA
�Ƃ��āA
�@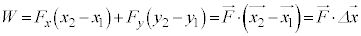
�����A�d���́A���̃x�N�g�����ψ��x�N�g���Ƃ̓��ςɓ������Ȃ�܂��B���̌������ψ��̌����̂Ȃ��p��θ �Ƃ���ƁA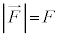 �C
�C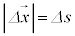 �Ƃ��āA
�Ƃ��āA
�@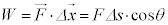
���̌������ψ��̌����Ƃ����p�ɂȂ�ꍇ�́A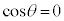 �ƂȂ�A
�ƂȂ�A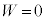 �ƂȂ�܂��B�܂�A�����ړ��̌����Ɛ����ɓ����ꍇ�ɂ́A���������d�������܂���B
�ƂȂ�܂��B�܂�A�����ړ��̌����Ɛ����ɓ����ꍇ�ɂ́A���������d�������܂���B
���̌������ψ��̌���������(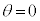 )�Ƃ��ɂ́A
)�Ƃ��ɂ́A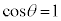 �ƂȂ�A
�ƂȂ�A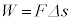 �ƂȂ�܂��B�܂�A�d�������~�ψ��ł��B
�ƂȂ�܂��B�܂�A�d�������~�ψ��ł��B
���̌������ψ��̌��������傤�Ƌt����(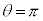 )�̂Ƃ��ɂ́A
)�̂Ƃ��ɂ́A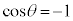 �ƂȂ�A
�ƂȂ�A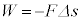 �ƂȂ�B���̂Ƃ��ɂ́A���͕����d�������܂��B�܂�A�^���G�l���M�[�����������铭�������܂��B
�ƂȂ�B���̂Ƃ��ɂ́A���͕����d�������܂��B�܂�A�^���G�l���M�[�����������铭�������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 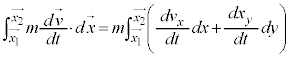 ����B
����B