�d�ׂ��A���I�ɕ��z����ꍇ�̃K�E�X�̖@��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����^�̃K�E�X�̖@���F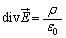
�����̓d�ׂ����݂���ꍇ�̃K�E�X�̖@���̍��ŋ��߂�
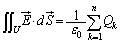 �@����@
�@����@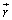 �Ŏw�肳���ʒu�̔����̐ϕ���
�Ŏw�肳���ʒu�̔����̐ϕ���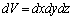 �����x
�����x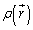 ���d�������݂���ꍇ�A���̔����̐ϓ����d����
���d�������݂���ꍇ�A���̔����̐ϓ����d����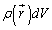 �ł���A�����d�ׂ����݂���̈�V(�Ȗ�U�ň͂܂ꂽ�̈�)�ɓn���đ̐ϕ�������S�d���ɂȂ�܂��B
�ł���A�����d�ׂ����݂���̈�V(�Ȗ�U�ň͂܂ꂽ�̈�)�ɓn���đ̐ϕ�������S�d���ɂȂ�܂��B
�܂�A�@��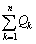 ��
��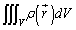 �ƍl���邱�Ƃ��ł��܂��B
�ƍl���邱�Ƃ��ł��܂��B
�K�E�X�̒藝�ɂ��A�@�̍��ӂ́A
����āA�@�́A�d�����A���I�ɕ��z����ꍇ�ɂ́A
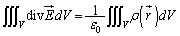 �@����A
�@����A
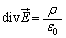 �@����A
�@����A
�A���́A��ԓ��ɕ��z����S�Ă��d������d�C�ʂ�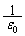 �{�̖{�����d�C�͐����o�čs��(���d�ׂȂ�I�[����)���Ƃ��Ӗ����Ă��܂��B�A���E�ӂ�ρ���d�ז��x�ł����A�d�E
�{�̖{�����d�C�͐����o�čs��(���d�ׂȂ�I�[����)���Ƃ��Ӗ����Ă��܂��B�A���E�ӂ�ρ���d�ז��x�ł����A�d�E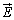 ���d�C�͐��̖��x�ł��邱�Ƃɒ��ӂ��Ă��������B
���d�C�͐��̖��x�ł��邱�Ƃɒ��ӂ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B