複数の電荷が存在する場合のガウスの法則
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
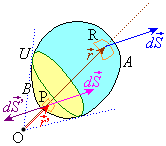原点Oに置かれた電荷Qが凸な閉曲面Uの外側にあるとき、原点Oから閉曲面に接線を引き、接点が作る曲線を境界として、閉曲面を原点から遠い側Aと近い側Bに分けます。
A上の各点Rと原点Oとを半直線ORで結ぶと、半直線ORは、閉曲面UのB側ともう一つ交点Pを持ちます。
，
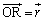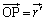として、R，Pにおける電界は、
，
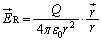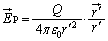より、曲面A，曲面Bにおける電界の面積分を考えます。曲面Aについては、
曲面Bについての面積分では面積素片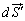
は、閉曲面Uの内側から外側に向くのですが、原点O側から曲面Bを見るとき(このときの曲面を
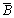とします)の面積素片は、
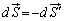となるので、
ところで、Aの立体角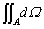
と
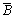の立体角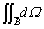
とは等しいので、閉曲面全体では、
つまり、閉曲面Uの外側の電荷は、面積分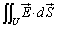
には寄与しません。面積分
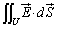に寄与するのは、閉曲面Uの内側の電荷だけです。
閉曲面Uの中に複数の電荷が存在する場合、ここで一つの仮定を置きます。空間内の電界は、各電荷が空間内の各点に作る電界を足し合わせたものだとします。これを重ね合わせの原理と言います。電界はベクトルなので、当然、ベクトル的に足し合わせることになります。
閉曲面U内に、n個の電荷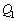
，
，･･･，
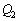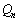が存在する場合には、電荷が閉曲面内のどこにあっても、
となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
