��啨��'01�N�O��[2]
�����ƃ}�C�N���z�������������B�}�C�N���z���͎����g(���x�ω��̔g)�̐U��A ( )�C�U����f�C�ʑ��𑪒肷�邱�Ƃ��ł���(�ʑ��Ƃ́At�������Ƃ��Ĕg�`��
)�C�U����f�C�ʑ��𑪒肷�邱�Ƃ��ł���(�ʑ��Ƃ́At�������Ƃ��Ĕg�`��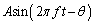 �ƕ\�����Ƃ���
�ƕ\�����Ƃ��� �̂��Ƃł���)�B�����̂Ƃ���ł̔g�`��
�̂��Ƃł���)�B�����̂Ƃ���ł̔g�`��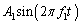 �ŕ\�����B������V�Ƃ��āA�ȉ��̖��ɓ�����B
�ŕ\�����B������V�Ƃ��āA�ȉ��̖��ɓ�����B
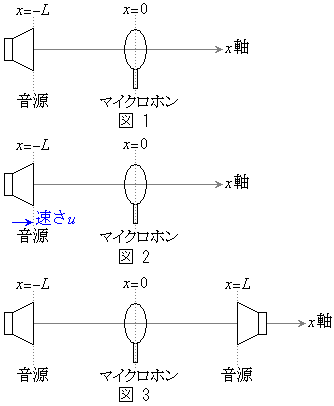 �T�@�}1�̂悤�ɉ�����
�T�@�}1�̂悤�ɉ�����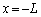 �ɁA�}�C�N���z�������_�ɌŒ肷��B
�ɁA�}�C�N���z�������_�ɌŒ肷��B��1�@�}�C�N���z���ő��肵���g�`��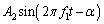 �ł������Bα��L�C
�ł������Bα��L�C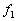 �CV��p���ĕ\���B
�CV��p���ĕ\���B �U�@�}2�̂悤�ɁA���_�Ƀ}�C�N���z�����Œ肵����ԂŁA������x���̐��̕����ɑ���u ( )�œ����Ă���B����
)�œ����Ă���B����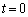 �ɉ�����
�ɉ�����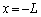 ��ʉ߂����B
��ʉ߂����B ��2�@����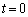 �ɉ�������o�����g���A�}�C�N���z���ɓ��B���鎞�������߂�B
�ɉ�������o�����g���A�}�C�N���z���ɓ��B���鎞�������߂�B ��3�@�}�C�N���z���ő��肵���g�`��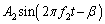 �ł������Bβ ��L�C
�ł������Bβ ��L�C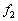 �CV��p���ĕ\���B
�CV��p���ĕ\���B ��4�@����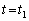 �ɉ�������o�����g���A�}�C�N���z���ɓ��B���鎞��
�ɉ�������o�����g���A�}�C�N���z���ɓ��B���鎞��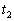 �����߂�B�������A����
�����߂�B�������A���� �ʼn�����x���̕��̗̈�ɂ�����̂Ƃ���B
�ʼn�����x���̕��̗̈�ɂ�����̂Ƃ���B ��5�@����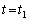 �ɉ�������o�����g�̈ʑ��ƁA����
�ɉ�������o�����g�̈ʑ��ƁA���� �Ƀ}�C�N���z���������g�̈ʑ����ׂ邱�Ƃɂ��
�Ƀ}�C�N���z���������g�̈ʑ����ׂ邱�Ƃɂ��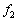 ��
�� �̊W�����߂�B�̍ۂɂ͌v�Z�̉ߒ����Ȍ��ɋL���B
�̊W�����߂�B�̍ۂɂ͌v�Z�̉ߒ����Ȍ��ɋL���B �V�@�}3�̂悤�ɁA2��̉��������ꂼ��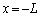 ��
��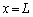 �ɌŒ肵���B���ꂼ��̉������P�Ƃɉ����o�����Ƃ��A���_�ɒu�����}�C�N���z���ő��肵���g�`�͂ǂ���������ŁA
�ɌŒ肵���B���ꂼ��̉������P�Ƃɉ����o�����Ƃ��A���_�ɒu�����}�C�N���z���ő��肵���g�`�͂ǂ���������ŁA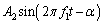 �ł������B
�ł������B ��6�@�����̉����������ɉ����o�����B�}�C�N���z���ő��肷��g�`�����߂�B�������A�����ł�α�͂��̂܂ܗp���Ă悢�B
��7�@���Ƀ}�C�N���z���̈ʒu��x���̐��̕����ɏ������点�đ��肵���Ƃ���A�U����0�ɂȂ����B���̂Ƃ��̃}�C�N���z����x���W��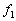 �CV��p���ĕ\���B�������A���̈ʒu�͌��_�ɍł��߂��U����0�ɂȂ�ʒu�ł���B�܂��A�Е��̉��������������o���Ă���Ƃ��A�}�C�N���z�����������炢�������Ă��A�}�C�N���z���ő��肷��U���͕ω����Ȃ��ƍl���Ă悢�B
�CV��p���ĕ\���B�������A���̈ʒu�͌��_�ɍł��߂��U����0�ɂȂ�ʒu�ł���B�܂��A�Е��̉��������������o���Ă���Ƃ��A�}�C�N���z�����������炢�������Ă��A�}�C�N���z���ő��肷��U���͕ω����Ȃ��ƍl���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���g�̊�{�����h�b�v���[�����̌��������A�Ƃ������ł��B
�Ȃ��A�g�������A�ʑ����Q�Ƃ��Ă��������B
�T�@��1 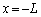 �Ɉʒu���鉹�����o�����g������V�Ői���
�Ɉʒu���鉹�����o�����g������V�Ői���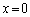 �Ɉʒu����}�C�N���z���ɓ͂��̂ɁA����
�Ɉʒu����}�C�N���z���ɓ͂��̂ɁA����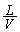 ��v���܂��B�]���āA�}�C�N���z���ő��肵���g�`�ł́A�����ł��ʑ�
��v���܂��B�]���āA�}�C�N���z���ő��肵���g�`�ł́A�����ł��ʑ�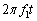 ������
������ �x���
�x���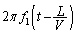 �ƂȂ�܂��B
�ƂȂ�܂��B �� 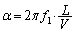 ......[��]
......[��]
�U�@��2 �������o�Ă��܂��A���g�͉����̈ړ��̉e���͎܂���B��1�Ɠ��l������ �������ă}�C�N���z���ɓ��B����̂ŁA�}�C�N���z���ɓ��B���������́A
�������ă}�C�N���z���ɓ��B����̂ŁA�}�C�N���z���ɓ��B���������́A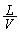 ......[��]
......[��]
��3 ������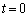 �ɏo�����g��
�ɏo�����g��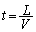 �Ƀ}�C�N���z���ɓ��B����̂ŁA��1�Ɠ��l�ɁA
�Ƀ}�C�N���z���ɓ��B����̂ŁA��1�Ɠ��l�ɁA �� 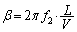 ......[��]
......[��]
��4 ���� �ɉ�����
�ɉ����� (
( )�ɗ��Ă��܂��B�����ʼn������o�����g������
)�ɗ��Ă��܂��B�����ʼn������o�����g������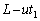 �i��Ń}�C�N���z���ɓ��B���܂��B���B����܂ł�������
�i��Ń}�C�N���z���ɓ��B���܂��B���B����܂ł�������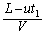 �C���B���������́A
�C���B���������́A 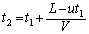 ......[��]
......[��]
��5 ��4�ɂ����āA �ɂ����鉹�����ʑ�
�ɂ����鉹�����ʑ� ��
�� �ɂ�����}�C�N���z���ɂ������ʑ�
�ɂ�����}�C�N���z���ɂ������ʑ� �͓������Ȃ�܂��B�܂�A
�͓������Ȃ�܂��B�܂�A ��  ......[��]
......[��]  ���D
���D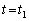 �ɂ����鉹�����ʑ�
�ɂ����鉹�����ʑ�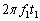 ��
�� �ɂ�����}�C�N���z���ɂ������ʑ�
�ɂ�����}�C�N���z���ɂ������ʑ�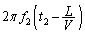 ���������Ȃ�A�Ƃ����Ӗ����킩��Â炢�����m��܂���B�E�}�̂悤�ɁA�h�b�v���[���ʂɂ��A�������o���Ƃ��̐U����
���������Ȃ�A�Ƃ����Ӗ����킩��Â炢�����m��܂���B�E�}�̂悤�ɁA�h�b�v���[���ʂɂ��A�������o���Ƃ��̐U����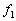 �ƃ}�C�N���z�����ϑ�����U����
�ƃ}�C�N���z�����ϑ�����U����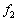 ���قȂ�̂ł����A
���قȂ�̂ł����A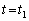 �̂Ƃ��ɉ������o���U����
�̂Ƃ��ɉ������o���U����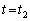 �Ƀ}�C�N���z���ɓ��B����킯�ł��B�ʑ����������Ȃ�A�Ƃ����̂́A
�Ƀ}�C�N���z���ɓ��B����킯�ł��B�ʑ����������Ȃ�A�Ƃ����̂́A �ɉ������o���Ƃ��̉��g�̐U�����g�P���̂ǂ̕ӂɂ����邩�A�Ƃ������ƂƁA
�ɉ������o���Ƃ��̉��g�̐U�����g�P���̂ǂ̕ӂɂ����邩�A�Ƃ������ƂƁA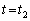 �Ƀ}�C�N���z���ɓ��B�����Ƃ��̉��g�̐U�����g1���̂ǂ̕ӂɂ����邩�A�Ƃ������Ƃ������ɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
�Ƀ}�C�N���z���ɓ��B�����Ƃ��̉��g�̐U�����g1���̂ǂ̕ӂɂ����邩�A�Ƃ������Ƃ������ɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
�V�@��6�@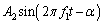 �ƂȂ�2�g���d�ˍ��킳���̂ŁA
�ƂȂ�2�g���d�ˍ��킳���̂ŁA 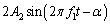 ......[��]
......[��]
��7�@��6�ł�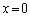 �Ɉʒu����}�C�N���z�������g�����瓙�����ɂ����āA2�g�͋��ߍ����܂����B
�Ɉʒu����}�C�N���z�������g�����瓙�����ɂ����āA2�g�͋��ߍ����܂����B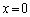 ��2�g�������g�̕��ɂȂ��Ă��܂��B���g�łׂ͗荇�����ƕ����������g����
��2�g�������g�̕��ɂȂ��Ă��܂��B���g�łׂ͗荇�����ƕ����������g���� �C�ׂ荇�����Ɛ߂��������g����
�C�ׂ荇�����Ɛ߂��������g����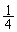 �ł��B
�ł��B ���g���g���� �Ȃ̂ŁA���߂�x���W�́A
�Ȃ̂ŁA���߂�x���W�́A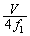 ......[��]�ʉ��D���̉���������Wx�Ɉʒu����}�C�N���z���ɓ��B����g�́A
......[��]�ʉ��D���̉���������Wx�Ɉʒu����}�C�N���z���ɓ��B����g�́A
�E�̉���������Wx�Ɉʒu����}�C�N���z���ɓ��B����g�́A 2�g���d�ˍ��킹��ƁA
2�g���d�ˍ��킹��ƁA ���Wx�ɂ������U����0�ɂȂ�̂ŁA
m�𐮐��Ƃ��āA
�� 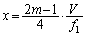
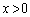 �ɂ�����
�ɂ�����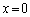 �ɍł��߂��̂�
�ɍł��߂��̂�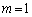 �̏ꍇ�ŁA
�̏ꍇ�ŁA ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B