波の干渉 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
複数の地点から発せられた波が重なり合って(重ね合わせの原理を参照)、強め合ったり弱め合ったりする現象を干渉と言う。
2波源から同位相の波が出るとき、経路差が波長の整数倍であれば強め合い、波長の整数倍から半波長ずれれば弱め合う。
2波源から逆位相の波が出るとき、強弱の条件は、同位相のときと逆になる。
波源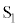 ,
,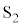 からP点まで波長λ,周期T,振幅Aの波が届くとします。
からP点まで波長λ,周期T,振幅Aの波が届くとします。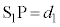 ,
,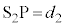 として、2つの波の式を、
として、2つの波の式を、
とします。
P点で観測される波は両波が合成された波です。観測される波の変位は、
この式のうち、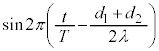 の部分は時間tを含むので、周期Tの単振動を表しています。単振動の振幅は、
の部分は時間tを含むので、周期Tの単振動を表しています。単振動の振幅は、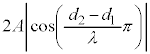 (時間tを含んでいないので、一つの決まった点で見ていれば一定の値となる)です。
(時間tを含んでいないので、一つの決まった点で見ていれば一定の値となる)です。
この振幅は、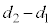 の値によって変化します。
の値によって変化します。
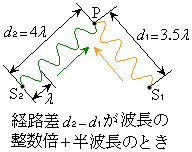 (1)
(1) 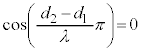 ,つまり、
,つまり、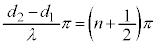 (n:整数)となるところでは、単振動の振幅は0です。
(n:整数)となるところでは、単振動の振幅は0です。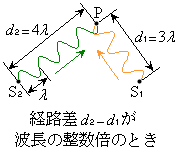 (2)
(2) 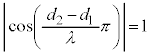 ,つまり、
,つまり、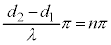 (n:整数)となるところでは、単振動の振幅は最大になります。
(n:整数)となるところでは、単振動の振幅は最大になります。このとき、経路差: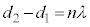 となります。波長の整数倍になっていることに注意してください。
となります。波長の整数倍になっていることに注意してください。
波源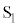 ,
,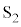 からやってくる2つの波は、ちょうど同じ変化の仕方をするようにしてP点に届きます。このときP点に届いた2つの波の関係を同位相と言います(波の位相を参照)。2つの波は同じ波形をしているので、強め合って振幅が最大となるのです。
からやってくる2つの波は、ちょうど同じ変化の仕方をするようにしてP点に届きます。このときP点に届いた2つの波の関係を同位相と言います(波の位相を参照)。2つの波は同じ波形をしているので、強め合って振幅が最大となるのです。
以上では、波源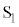 ,
,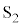 からやってくる2つの波について、波源から出るときに同じ波形になるように出る(波源で同位相)場合を考えました。
からやってくる2つの波について、波源から出るときに同じ波形になるように出る(波源で同位相)場合を考えました。
もし、波源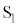 ,
,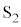 からやってくる2つの波が、波源から出るときに逆位相だとどういうことになるでしょうか?このときは、2つの波の式は、
からやってくる2つの波が、波源から出るときに逆位相だとどういうことになるでしょうか?このときは、2つの波の式は、
となります。P点で観測される波は、
となります。今度は、単振動を表す部分が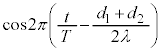 ,振幅が
,振幅が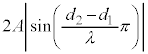 です。
です。
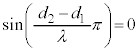 となるのは、経路差:
となるのは、経路差: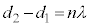 (n:整数)の場合です。このとき、単振動の振幅は0です。
(n:整数)の場合です。このとき、単振動の振幅は0です。
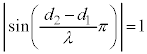 となるのは、経路差:
となるのは、経路差: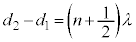 (n:整数)の場合です。このとき、単振動の振幅は最大です。
(n:整数)の場合です。このとき、単振動の振幅は最大です。
結局、2波源から同位相の波が出るときと、逆位相の波が出るときとでは、強弱が入れ替わることがわかります。
重要なポイントは、観測地点に同位相の2波がたどりつくときには強め合い、逆位相の2波がたどりつくときには弱め合うということです。無理に覚え込もうとせずに、波の絵を描いて理解するように努力してください。
整理すると、2波源から同位相の波が出るとき、経路差が波長の整数倍であれば強め合い、波長の整数倍から半波長ずれれば弱め合います。
2波源から逆位相の波が出るとき、経路差が波長の整数倍であれば弱め合い、波長の整数倍から半波長ずれれば強め合います。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 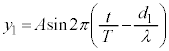 ,
,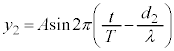
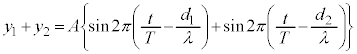
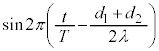 の部分は時間tを含むので、周期Tの単振動を表しています。単振動の振幅は、
の部分は時間tを含むので、周期Tの単振動を表しています。単振動の振幅は、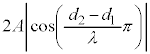 (時間tを含んでいないので、一つの決まった点で見ていれば一定の値となる)です。
(時間tを含んでいないので、一つの決まった点で見ていれば一定の値となる)です。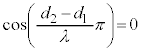 ,つまり、
,つまり、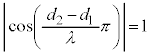 ,つまり、
,つまり、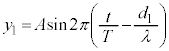 ,
,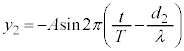
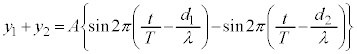
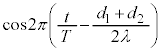 ,振幅が
,振幅が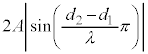 です。
です。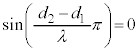 となるのは、経路差:
となるのは、経路差: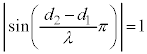 となるのは、経路差:
となるのは、経路差: