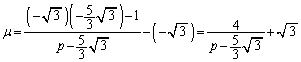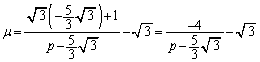��啨��'07�N�O��[1]
 �}�̂悤�ɁA����
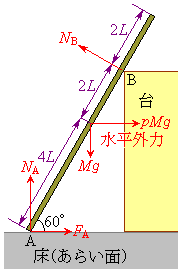
�}�̂悤�ɁA���� �C����M�ׂ̍���l�ȍ��̖_���A�����ȏ��̏�ɏ��Ɗp�x
�C����M�ׂ̍���l�ȍ��̖_���A�����ȏ��̏�ɏ��Ɗp�x �ƂȂ�悤�ɒu����A��[����
�ƂȂ�悤�ɒu����A��[����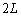 �̈ʒu�ő�̃J�h�Ɛڂ���悤�ɗ��Ă����Ă���B��̃J�h�͊��炩�ŁA�_�Ƃ̊Ԃɖ��C�͓͂����Ȃ��B���ʂ͂��炭�A�_�Ƃ̊Ԃɖ��C�͂������B�_�����ʂɐڂ���_��A�Ƃ��AA�ɂ����Ė_��������鐂���R�͂̑傫����
�̈ʒu�ő�̃J�h�Ɛڂ���悤�ɗ��Ă����Ă���B��̃J�h�͊��炩�ŁA�_�Ƃ̊Ԃɖ��C�͓͂����Ȃ��B���ʂ͂��炭�A�_�Ƃ̊Ԃɖ��C�͂������B�_�����ʂɐڂ���_��A�Ƃ��AA�ɂ����Ė_��������鐂���R�͂̑傫����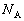 �C���C�͂�
�C���C�͂�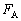 �Ƃ���B�܂��A�_����̃J�h�Ɛڂ���_��B�Ƃ��A�_�ɐ����ȕ����ɓ���B�ɂ�����R�͂̑傫����
�Ƃ���B�܂��A�_����̃J�h�Ɛڂ���_��B�Ƃ��A�_�ɐ����ȕ����ɓ���B�ɂ�����R�͂̑傫���� �Ƃ���B
�Ƃ���B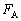 �̐��̕����͐}�Ɏ������̌����Ƃ���B�܂��A�_�Ə��ʂ̊Ԃ̐Î~���C�W����μ�C�d�͉����x��g�Ƃ���B�_�̒��S�ɂ͏d��
�̐��̕����͐}�Ɏ������̌����Ƃ���B�܂��A�_�Ə��ʂ̊Ԃ̐Î~���C�W����μ�C�d�͉����x��g�Ƃ���B�_�̒��S�ɂ͏d��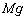 �������B
�������B
�T�D�����ȊO�͂�_�̒��S�ɉ������Ƃ���A�_�͐Î~�����܂܂ł������B�������A�����O�͂̑傫���͖_�̏d����p�{( )�Ƃ��A�E�����ɓ����Ƃ���
)�Ƃ��A�E�����ɓ����Ƃ��� �Ƃ���B
�Ƃ���B ��1�@�_�ɓ����͂́A�_A�̂܂��̃��[�����g�̂肠�����A ���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B
���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B ��2�@�_�ɓ����͂̂肠�����A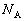 ���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B
���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B ��3�@�_�ɓ����͂̂肠�����A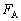 ���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B
���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B ��4�@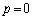 �̂Ƃ��ɖ_���Î~���Ă��邽�߂�μ�͈̔͂����߂�B
�̂Ƃ��ɖ_���Î~���Ă��邽�߂�μ�͈̔͂����߂�B �U�D���ɁA�_�������Ȃ��悤�Ɏ�Ŏx���Ă���A�_�̒��S�ɐ����O�͂��������B���_��������ƁA�����O��( )�ƐÎ~���C�W��(μ)�̑傫���ɉ����āA�_�͐Î~�����܂܂��^�����n�߂邩�̂����ꂩ�ł���B�_���Î~�����܂܂ł��邽�߂ɂ́A����3�̏����������ɖ�������Ȃ���Ȃ�Ȃ��B
)�ƐÎ~���C�W��(μ)�̑傫���ɉ����āA�_�͐Î~�����܂܂��^�����n�߂邩�̂����ꂩ�ł���B�_���Î~�����܂܂ł��邽�߂ɂ́A����3�̏����������ɖ�������Ȃ���Ȃ�Ȃ��B (����a)�@��̃J�h(�_B)����_������Ȃ��B
(����b)�@������_������Ȃ��B
(����c)�@���ɐڂ���_�̒[�������ɂ��E�ɂ����ׂ�Ȃ��B
���̏ꍇ�A����b�́A����c����������Ă���Ƃ��ɂ́A�K����������Ă���B
��5�@�������̑傫�Ȑ����O��(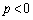 )���������Ƃ��ɁA����a���j��Ă��܂��B����a����������邽�߂́Ap�͈̔͂����߂�B
)���������Ƃ��ɁA����a���j��Ă��܂��B����a����������邽�߂́Ap�͈̔͂����߂�B ��6�@���̐Î~���C�W�����������Ƃ��ɏ���c���j��Ă��܂��B�_�̉��[�����ɂ��ׂ�Ȃ����߂�μ�C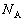 �C
�C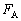 ���������ׂ���������K���Ɏ��ό`����ƁAp��μ�̊Ԃ̊W���Ƃ��Ď��̂悤�ɕ\����B(1)�C(2)�C(3)�ɓK���Ȑ�������B
���������ׂ���������K���Ɏ��ό`����ƁAp��μ�̊Ԃ̊W���Ƃ��Ď��̂悤�ɕ\����B(1)�C(2)�C(3)�ɓK���Ȑ�������B ��7�@���l�ɂ��āA�_�̉��[���E�ɂ��ׂ�Ȃ����߂�p��μ���������ׂ������͎����ŕ\����B(4)�C(5)�C(6)�ɓK���Ȑ�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�͂̃��[�����g�̖��ł��B�U�����e�ŁA�w���ʂ�ɂ���Ă����Ήł��܂����A�U�����Ȃ��Ă��ł���悤�ɂ��Ă��������Ƃ���ł��B
����a)�Cb)�Cc)���^�����Ă���̂́A�Z�I�ȂLjËL���Ă��Ȃ��Ă��ǂ��A�Ƃ������b�Z�[�W�Ȃ̂ł��傤����ǂ��A���ꂭ�炢�͒m���Ƃ��Ă����Ă���ׂ����Ǝv���܂��B
�T�D��1�@�_A�̂܂����͂̃��[�����g���l����̂ŁA ��
��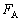 �����ł̒���(�_A�������̍�p���ɉ��낵�������̒���)��0�ōl����K�v�͂���܂���B
�����ł̒���(�_A�������̍�p���ɉ��낵�������̒���)��0�ōl����K�v�͂���܂���B �d�� (���v���)�����ł̒�����
(���v���)�����ł̒�����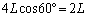 �C�����O��
�C�����O��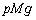 (���v���)�����ł̒�����
(���v���)�����ł̒�����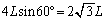 �C�R��
�C�R��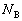 (�����v���)�����ł̒�����
(�����v���)�����ł̒����� �C����āA�_A�̂܂������̃��[�����g�̂荇����(�����v���𐳂Ƃ���)�A
�C����āA�_A�̂܂������̃��[�����g�̂荇����(�����v���𐳂Ƃ���)�A �� 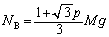 ......[��]
......[��]
��2�@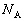 �����߂邽�߂ɂ͉������������̂荇�����l���܂��B���������ɓ������������R��
�����߂邽�߂ɂ͉������������̂荇�����l���܂��B���������ɓ������������R��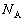 (�����)�̂ق��ɁA�d��
(�����)�̂ق��ɁA�d��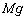 (������)�C�R��
(������)�C�R��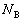 �̉�����������
�̉�����������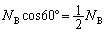 (�����)�C����āA�����������͂̂荇���́A
(�����)�C����āA�����������͂̂荇���́A ��1�̌��ʂ�p���āA
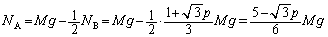 ......[��]
......[��]
��3�@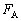 �����߂邽�߂ɂ͐������������̂荇�����l���܂��B���������ɓ��������Î~���C��
�����߂邽�߂ɂ͐������������̂荇�����l���܂��B���������ɓ��������Î~���C��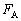 (�����͂킩��Ȃ��A�����Ƃ����肤��)�̂ق��ɁA�����O��
(�����͂킩��Ȃ��A�����Ƃ����肤��)�̂ق��ɁA�����O�� (�E����)�C�R��
(�E����)�C�R��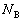 �̐�����������
�̐�����������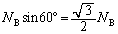 (������)�C����āA�����������͂̂荇���́A
(������)�C����āA�����������͂̂荇���́A ��1�̌��ʂ�p���āA
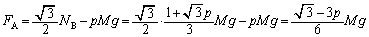 ......[��]
......[��]
��4�@ �������O�����Ȃ��A�_A�Ŗ_�̉��[�͍����ɂ��ׂ낤�Ƃ��Ă���̂ŁA�_���Î~���Ă��邽�߂ɂ́A�_A�ʼnE�������Î~���C��
�������O�����Ȃ��A�_A�Ŗ_�̉��[�͍����ɂ��ׂ낤�Ƃ��Ă���̂ŁA�_���Î~���Ă��邽�߂ɂ́A�_A�ʼnE�������Î~���C��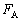 ���ő�Î~���C��
���ő�Î~���C�� �ȉ��ł��邱�Ƃ��K�v�\��(���C�����Q��)�ł��B
�ȉ��ł��邱�Ƃ��K�v�\��(���C�����Q��)�ł��B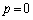 �̂Ƃ��A
�̂Ƃ��A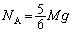 �C
�C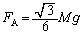
�� 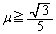
�U�D��5�@��̃J�h(�_B)����_������Ȃ������́A
��  ......[��]
......[��]
��6�@�_�̉��[�������ɂ��ׂ�Ȃ������́A�E�������Î~���C�� ���ő�Î~���C��
���ő�Î~���C��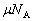 �ȉ��ł��邱�Ƃł��B
�ȉ��ł��邱�Ƃł��B 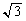 �Ŋ��萮������ƁA
�Ŋ��萮������ƁA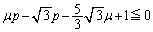 �@����@
�@����@(1)  �C(2)
�C(2) 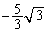 �C(3) 1 ......[��]
�C(3) 1 ......[��]
��7�@�_�̉��[���E���ɂ��ׂ�Ȃ������́A���������Î~���C��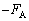 ���ő�Î~���C��
���ő�Î~���C��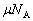 �ȉ��ł��邱�Ƃł��B
�ȉ��ł��邱�Ƃł��B  �Ŋ��萮������ƁA
�Ŋ��萮������ƁA �@����A
�@����A(4) 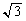 �C(5)
�C(5)  �C(6)
�C(6)  ......[��]
......[��]
��8�@�̈��}������ۂ� �ł��邱�Ƃɒ��ӂ��܂��B
�ł��邱�Ƃɒ��ӂ��܂��B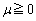 �Ɩ�5�̌��ʁC��6�̌��ʇ@�C��7�̌��ʇA�����ׂĖ������A�_���Î~�����܂܂ɂȂ�܂��B
�Ɩ�5�̌��ʁC��6�̌��ʇ@�C��7�̌��ʇA�����ׂĖ������A�_���Î~�����܂܂ɂȂ�܂��B �@�̋��E��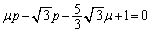 �@����B�@�ɑ��āA��蕶�Ɏw�肳��Ă���悤�ȕό`���s���ƁA
�@����B�@�ɑ��āA��蕶�Ɏw�肳��Ă���悤�ȕό`���s���ƁA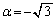 �C
�C �C
�C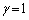 �Ƃ��āA
�Ƃ��āA ����́A �C
�C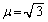 ��Q�ߐ��Ƃ����o�Ȑ��ł��B
��Q�ߐ��Ƃ����o�Ȑ��ł��B
�@�́A �̂Ƃ��A
�̂Ƃ��A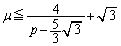 �@����C
�@����C
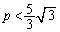 �̂Ƃ��A
�̂Ƃ��A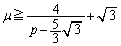 �@����D
�@����D
�A�̋��E��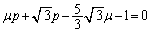 �ɑ��āA��蕶�Ɏw�肳��Ă���悤�ȕό`���s���ƁA
�ɑ��āA��蕶�Ɏw�肳��Ă���悤�ȕό`���s���ƁA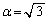 �C
�C �C
�C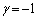 �Ƃ��āA
�Ƃ��āA ����́A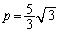 �C
�C ��Q�ߐ��Ƃ���o�Ȑ��ł�(�B��p���Ɋւ��đΏ�)�B
��Q�ߐ��Ƃ���o�Ȑ��ł�(�B��p���Ɋւ��đΏ�)�B
�A�́A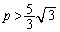 �̂Ƃ��A
�̂Ƃ��A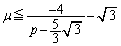 �@����E
�@����E
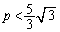 �̂Ƃ��A
�̂Ƃ��A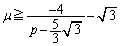 �@����F
�@����F
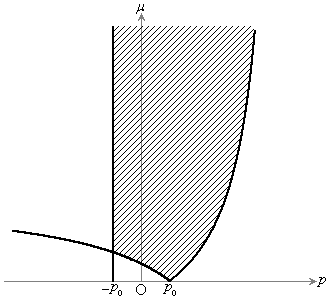 ��L�ŁA
��L�ŁA �̂Ƃ��A�C���E�����K�v������܂����A�E���
�̂Ƃ��A�C���E�����K�v������܂����A�E���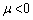 �ɂȂ��Ă��܂��̂ŁA
�ɂȂ��Ă��܂��̂ŁA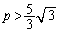 �̂Ƃ��ɂ͏������݂���μ�͑��݂��܂���B
�̂Ƃ��ɂ͏������݂���μ�͑��݂��܂���B
���ǁA���߂�̈�́A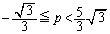 ���D���F�̕����ƂȂ�A�}������ƉE�}�ΐ���(���E�����܂�)�B
���D���F�̕����ƂȂ�A�}������ƉE�}�ΐ���(���E�����܂�)�B
�}����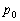 �́A�B��p���Ƃ̌�_�ŁA�B��
�́A�B��p���Ƃ̌�_�ŁA�B��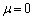 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A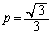 (��5�̌��ʂ̕�����ς������̂Ɉ�v)
(��5�̌��ʂ̕�����ς������̂Ɉ�v)  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B