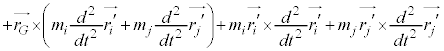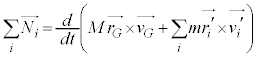�͂̃��[�����g�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
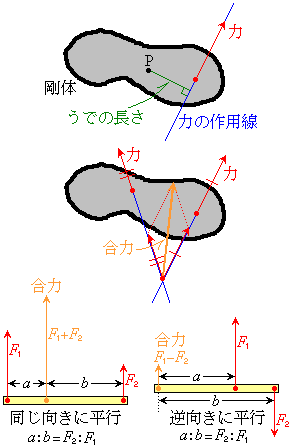 �����Ȃ������������Ă��ό`�����Ɍ��̌`���ۂ��̂������ƌ����B
�����Ȃ������������Ă��ό`�����Ɍ��̌`���ۂ��̂������ƌ����B
���̃x�N�g��������Ă��钼�����͂̍�p���ƌ����B
���������Ă����͕̂ό`���Ȃ��̂ŁA���̂ɂ��������́A���̍�p����̂ǂ��ōl���Ă��������ʂ��y�ڂ��B
����_P�����̍�p���Ƃ�����(�_�������̍�p���ɉ��낵������������)���A�����������ł̒����ƌ����B
���̑傫�������ł̒����̐ςɁA���������_P�̂܂��ɔ����v���ɍ��̂���]�����悤�Ƃ��Ă���Ƃ��ɐ��A���v���ɉ�]�����悤�Ƃ��Ă���Ƃ��ɕ��A�ƂȂ�悤�ȕ������������̂��A�͂̃��[�����g�ƌ����B
���̂Ɋւ���肠���̏����́A���̂ɓ������̘a����x�N�g���A���A�͂̃��[�����g�̘a����B
���̂ɓ��������������l����ꍇ�A���s�łȂ�2���̘a�́A���̍�p���̌�_�܂������ړ��������������l����B
���������ɕ��s��2���������́A���̑傫����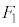 �C
�C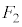 �C���̍�p���ɐ����Ȓ����Ƃ̌�_��
�C���̍�p���ɐ����Ȓ����Ƃ̌�_��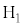 �C
�C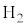 �Ƃ��āA
�Ƃ��āA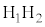 ��
��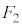 �F
�F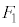 �ɓ�������_�ɁA2���Ɠ��������ő傫����
�ɓ�������_�ɁA2���Ɠ��������ő傫����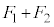 �����Ƃ��čl���邱�Ƃ��ł���B
�����Ƃ��čl���邱�Ƃ��ł���B
�t�����ɕ��s��2���������́A���̑傫����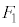 �C
�C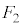 (
(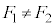 )�C���̍�p���ɐ����Ȓ����Ƃ̌�_��
)�C���̍�p���ɐ����Ȓ����Ƃ̌�_��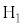 �C
�C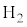 �Ƃ��āA
�Ƃ��āA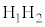 ��
��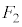 �F
�F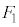 �ɊO������_�ɁA
�ɊO������_�ɁA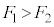 �Ȃ�
�Ȃ�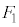 �̌����A
�̌����A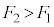 �Ȃ�
�Ȃ�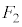 �̌����ŁA�傫����
�̌����ŁA�傫����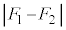 �����Ƃ��čl���邱�Ƃ��ł���B
�����Ƃ��čl���邱�Ƃ��ł���B
�t�����ɕ��s��2���̑傫�����������Ƃ��́A����2�����������邱�Ƃ͂ł��Ȃ��B���̏ꍇ��2���������ƌ����B�����́A���̂���]�^��������B���̑傫����2���̍�p���Ԃ������Ƃ̐ς����͂̃��[�����g�ƌ����B
�傫�����l����K�v�̂Ȃ����̂̉^���ł́A���̂�������������1�̓_(���_�ƌ����܂�)�ƍl���܂��B���̂Ƃ��́A���̂��Î~�������͓����x�^���𑱂���Ƃ��A���͂�0�Ƃ����͂̂肠�����l����悢�̂ł����A�傫�����l���镨�̂ł́A���̂��̂��̂̉�]�^�����l����K�v���o�Ă��܂��B
�]���āA���̂Ɋւ���肠���̏����ɂ́A��������x�N�g���ɂȂ�A�Ƃ��������łȂ��A��]���Ȃ������A�͂̃��[�����g�̘a��0�Ƃ���������t��������K�v������܂��B
(1) ���������ɕ��s��2���̍���
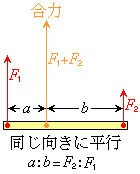 �E�}�ɂ����āA��������p���Ă���_����
�E�}�ɂ����āA��������p���Ă���_����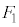 �C��
�C��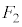 �̍�p���Ƃ�������a�Cb�Ȃ̂ŁA���̓_�̂܂����͂̃��[�����g�̂肠���̎��F
�̍�p���Ƃ�������a�Cb�Ȃ̂ŁA���̓_�̂܂����͂̃��[�����g�̂肠���̎��F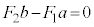
�� a�Fb = 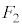 �F
�F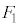
(2) �t�����ɕ��s��2���̍���
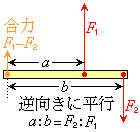 �E�}�ɂ����āA��������p���Ă���_����
�E�}�ɂ����āA��������p���Ă���_����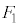 �C��
�C��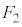 �̍�p���Ƃ�������a�Cb�Ȃ̂ŁA���̓_�̂܂����͂̃��[�����g�̂肠���̎��F
�̍�p���Ƃ�������a�Cb�Ȃ̂ŁA���̓_�̂܂����͂̃��[�����g�̂肠���̎��F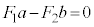
�� a�Fb = 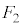 �F
�F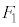
���̏ꍇ�ɂ́A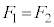 �̂Ƃ��A�O���_�����݂��Ȃ��Ȃ�̂ŁA2���������ł��܂���B����2�͂������ƌ����܂����A���̂���]�����铭�������܂�(�ȉ��ɏڏq���܂�)�B
�̂Ƃ��A�O���_�����݂��Ȃ��Ȃ�̂ŁA2���������ł��܂���B����2�͂������ƌ����܂����A���̂���]�����铭�������܂�(�ȉ��ɏڏq���܂�)�B
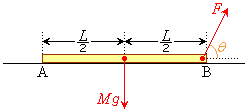 ���@�E�}�̂悤�ɁA����M�C����L�̈�l�Ȗ_�������ȏ��ɒu����Ă��āAB�[���A���ƂȂ��p��θ �̕����ɑ傫��F�̗͂ň�������B���Ɩ_�̊Ԃ̐Î~���C�W����μ���Ƃ��āA�_������o�����ƂȂ��AB�[�������オ�邽�߂̊pθ �̏��������߂�B
���@�E�}�̂悤�ɁA����M�C����L�̈�l�Ȗ_�������ȏ��ɒu����Ă��āAB�[���A���ƂȂ��p��θ �̕����ɑ傫��F�̗͂ň�������B���Ɩ_�̊Ԃ̐Î~���C�W����μ���Ƃ��āA�_������o�����ƂȂ��AB�[�������オ�邽�߂̊pθ �̏��������߂�B
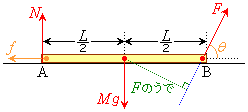 ���@B�[�������オ��u�ԂɁA�_��������������R��N�C�Î~���C��f�́AA�[�ɓ����܂��B
���@B�[�������オ��u�ԂɁA�_��������������R��N�C�Î~���C��f�́AA�[�ɓ����܂��B
�_���d���͖_�̒��S�ɓ����Ă��āA���̓_�ōl������F�����ł̒����́A�E�}�̂悤�ɁA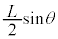 �C��F�̃��[�����g�́A
�C��F�̃��[�����g�́A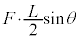 (�����v�܂��ɖ_�����Ƃ���̂Ő�)�ł��B
(�����v�܂��ɖ_�����Ƃ���̂Ő�)�ł��B
�_�ɓ��������������͂̂荇���F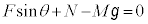 �@����@
�@����@
�_�ɓ��������������͂̂荇���F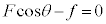 �@����A
�@����A
�_�̒��S�̂܂����͂̃��[�����g�̂荇���F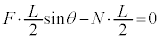 �@����B
�@����B
���Ɩ_�̊Ԃ�����o���Ȃ������F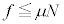 �@����C�@(���C�����Q��)
�@����C�@(���C�����Q��)
�@���A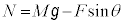 �@����D
�@����D
�B�ɑ�����āA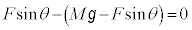
�� 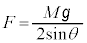
�D���A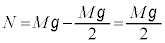
�A���A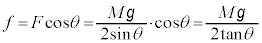
�C���A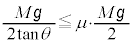
�� 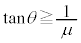 ......[��]
......[��]
��L�ɂ��āA�ڍׂɌ������Ă݂܂��B
����m�̕��̂���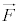 �������Ă���Ƃ��A���̂������x��
�������Ă���Ƃ��A���̂������x��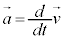 �Ƃ��āA
�Ƃ��āA
�^���������F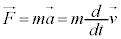
�̗��ӂ�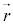 �Ƃ��O�����l���܂��B
�Ƃ��O�����l���܂��B
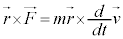 �@����@
�@����@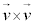 �͗�x�N�g���ɂȂ�܂��B�]���āA
�͗�x�N�g���ɂȂ�܂��B�]���āA
������A�@�̉E�ӂ́A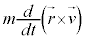 �Ə������Ƃ��ł��āA
�Ə������Ƃ��ł��āA
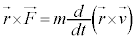 �@����A
�@����A
���ӂ�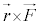 �̑傫���́A
�̑傫���́A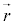 ��
��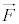 �̂Ȃ��p��θ (
�̂Ȃ��p��θ (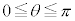 )�Ƃ��āA
)�Ƃ��āA
�ƂȂ�܂����A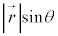 �́A��
�́A��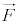 �����ł̒����Ȃ̂ŁA
�����ł̒����Ȃ̂ŁA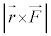 �́A��w�����̎����͈͂ɂ�������
�́A��w�����̎����͈͂ɂ�������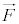 �̃��[�����g�ł��B
�̃��[�����g�ł��B
��ʓI�ɂ́A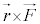 ���A��
���A��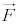 �̃��[�����g�ƌ����܂��B
�̃��[�����g�ƌ����܂��B
�����ƈ�ʓI�Ɍ����ƁA�ǂ�ȃx�N�g��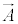 �ɂ��Ă��A
�ɂ��Ă��A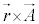 ���A�x�N�g��
���A�x�N�g��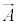 �̃��[�����g�ƌ����܂��B��w�����ɂ����Ă��A�P�Ɂu���[�����g�v�ƌ���Ȃ��ŁA��X�A�u�͂́v���[�����g�ƌ����̂́A���̂��߂ł��B
�̃��[�����g�ƌ����܂��B��w�����ɂ����Ă��A�P�Ɂu���[�����g�v�ƌ���Ȃ��ŁA��X�A�u�͂́v���[�����g�ƌ����̂́A���̂��߂ł��B
�A�̉E�ӂɏo�Ă���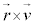 �̑傫���́A
�̑傫���́A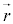 ��
��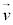 �̂Ȃ��p��φ (
�̂Ȃ��p��φ (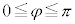 )�Ƃ��āA
)�Ƃ��āA
�ƂȂ�܂����A����́A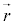 ��
��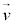 �ō��O�p�`�̖ʐς�2�{�ɂȂ��Ă��āA�P�v���[�̑�2�@���ɏo�Ă���ʐϑ��x��2�{�ɂȂ��Ă��܂��B
�ō��O�p�`�̖ʐς�2�{�ɂȂ��Ă��āA�P�v���[�̑�2�@���ɏo�Ă���ʐϑ��x��2�{�ɂȂ��Ă��܂��B
�P�v���[�̑�2�@���́A���̂ɓ����͂����S��(�˂ɁA����1��_��������)�ł���A�ʐϑ��x���ۑ������Ƃ����@���ł����āA�ʐϑ��x�͉�]�^���̐����̂悤�Ȃ��̂�\���Ă��܂��B��ʓI�ɂ́A�E���E�ӂ�����m������̒��ɓ���āA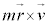 ���p�^�����ƌ����܂��B
���p�^�����ƌ����܂��B
�A���́A�p�^�����������ω����͂̃��[�����g�ɓ������A�͂̃��[�����g����]�^�����N�����ƌ����Ă��鎮�ł��B
�����ŁA���̂��l���A���̂�����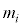 �̕����ɕ����čl���܂��B
�̕����ɕ����čl���܂��B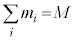 �͍��̑S�̂������ł��B
�͍��̑S�̂������ł��B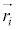 �Ɉʒu��������
�Ɉʒu��������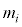 �̕�������
�̕�������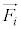 ���������Ă���Ƃ��܂��B���̕����̉^���������́A
���������Ă���Ƃ��܂��B���̕����̉^���������́A
���̗��ӂ����̑S�̂ő������킹�܂��B�e�����������͍��̂Ȃ̂������ω��͂Ȃ��A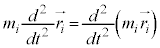 ���A
���A
���̂��l���Ă���̂ŁA���̂��d�S�ʒu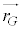 �͍��̓����ړ����邱�Ƃ͂Ȃ��A
�͍��̓����ړ����邱�Ƃ͂Ȃ��A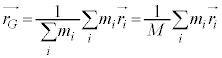 ���A
���A
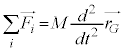 �@����B
�@����B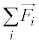 ���A���̂��S����M���d�S�ɏW�����Ă���Ƃ��āA���̂̕��i�^�����l����Ηǂ��A�Ƃ������Ƃ�\���Ă��܂��B�������Ȃ���A�������l����ꍇ�ɁA���̍�p�_��1�_�ɂ܂Ƃ߂��Ȃ���������܂��B����́A�������ɕ��s�œ���t��������(����)�̏ꍇ�ł��B
���A���̂��S����M���d�S�ɏW�����Ă���Ƃ��āA���̂̕��i�^�����l����Ηǂ��A�Ƃ������Ƃ�\���Ă��܂��B�������Ȃ���A�������l����ꍇ�ɁA���̍�p�_��1�_�ɂ܂Ƃ߂��Ȃ���������܂��B����́A�������ɕ��s�œ���t��������(����)�̏ꍇ�ł��B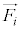 �̒��������ƂȂ���̂�����Ƃ��ɂ́A�B���ł͓s���������̂ŁA
�̒��������ƂȂ���̂�����Ƃ��ɂ́A�B���ł͓s���������̂ŁA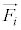 ��1�_�ɓ������Ƃ��Ă܂Ƃ߂�����̂ƁA�����ɂȂ��Ă��܂����̂ɕ����A���i�^���ɂ��ẮA�B�̍��ӂ�
��1�_�ɓ������Ƃ��Ă܂Ƃ߂�����̂ƁA�����ɂȂ��Ă��܂����̂ɕ����A���i�^���ɂ��ẮA�B�̍��ӂ�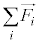 ���A�����ƂȂ�g�ݍ��킹�������������Ƃ��čl���܂��B
���A�����ƂȂ�g�ݍ��킹�������������Ƃ��čl���܂��B
�B���̍��ӂ̒��ɁA�����ƂȂ�g�ݍ��킹���c��ꍇ�A�܂�A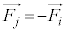 �Ƃ����W�ɂ���2��
�Ƃ����W�ɂ���2��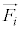 �C
�C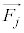 �Ƃ����͂��A
�Ƃ����͂��A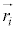 �C
�C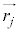 �ɓ����Ă���悤�ȑg�ݍ��킹���c��ꍇ�ɂ́A�B�̍��ӂ�
�ɓ����Ă���悤�ȑg�ݍ��킹���c��ꍇ�ɂ́A�B�̍��ӂ�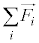 ���������ƂȂ���̂��������o���čl���邱�Ƃɂ��܂��B
���������ƂȂ���̂��������o���čl���邱�Ƃɂ��܂��B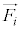 ���S�������ƂȂ����݂̂��Ƃ���ƁA
���S�������ƂȂ����݂̂��Ƃ���ƁA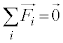 �ł�(���邢�́A�͂̂肠�����������Ă���ꍇ���l���܂�)�B���̏ꍇ�ɂ́A�B�́A���̂̏d�S���Î~�𑱂��邩�A�����x�^���𑱂���Ƃ������Ƃ������Ă��܂��B
�ł�(���邢�́A�͂̂肠�����������Ă���ꍇ���l���܂�)�B���̏ꍇ�ɂ́A�B�́A���̂̏d�S���Î~�𑱂��邩�A�����x�^���𑱂���Ƃ������Ƃ������Ă��܂��B
�������Ȃ���A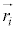 �C
�C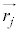 ����p�_�Ƃ���A�����ƂȂ�g�ݍ��킹��2��
����p�_�Ƃ���A�����ƂȂ�g�ݍ��킹��2��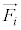 �C
�C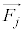 (
(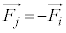 )�ɂ��ẮA�^���������F
)�ɂ��ẮA�^���������F
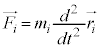 �C
�C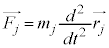
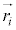 �C
�C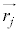 �Ƃ̊O�ς��Ƃ�ƁA
�Ƃ̊O�ς��Ƃ�ƁA
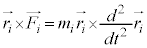 �C
�C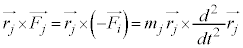
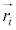 �C
�C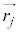 ���d�S���ʒu�x�N�g���Əd�S����̂���
���d�S���ʒu�x�N�g���Əd�S����̂���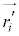 �C
�C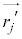 �ɕ����āA
�ɕ����āA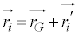 �C
�C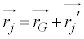 �Ə����A���҂̘a���Ƃ�ƁA
�Ə����A���҂̘a���Ƃ�ƁA
�܂��A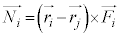 (���͂̃��[�����g�ƌ����܂�)�Ƃ����ƁA
(���͂̃��[�����g�ƌ����܂�)�Ƃ����ƁA
���̎��̗��ӂ����̑S�̂ɂ��đ������킹��ƁA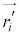 �C
�C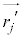 �͏d�S����������Ȃ̂ŁA
�͏d�S����������Ȃ̂ŁA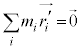 ���E�ӑ�2���̘a��
���E�ӑ�2���̘a��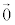 �C�܂��A
�C�܂��A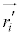 �������ω��̑��a��
�������ω��̑��a��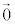 �ŁA�E�ӑ�3���̘a��
�ŁA�E�ӑ�3���̘a��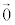 �ƂȂ�A��1���Ƒ�4���̘a�������c��A
�ƂȂ�A��1���Ƒ�4���̘a�������c��A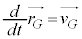 �C
�C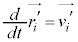 �Ƃ��ćA�����̂Ɠ������ό`���s���A
�Ƃ��ćA�����̂Ɠ������ό`���s���A
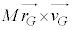 �͍��̂̏d�S���p�^�����ł��B
�͍��̂̏d�S���p�^�����ł��B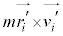 �͏d�S����e�����������Ƃ��̊e�������p�^�����ł��B���̂ɂ��ẮA�����̑��a���p�^�����������ω��ł���A�Ƃ��������l���ĉ�]�^�����l���邱�ƂɂȂ�܂��B���̂ɂ��ẮA����
�͏d�S����e�����������Ƃ��̊e�������p�^�����ł��B���̂ɂ��ẮA�����̑��a���p�^�����������ω��ł���A�Ƃ��������l���ĉ�]�^�����l���邱�ƂɂȂ�܂��B���̂ɂ��ẮA����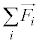 ����x�N�g���ł����Ă��A�����̘a
����x�N�g���ł����Ă��A�����̘a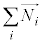 ����x�N�g���ɂȂ炸�ɉ�]�^�����s���ꍇ������܂��B
����x�N�g���ɂȂ炸�ɉ�]�^�����s���ꍇ������܂��B
�]���āA���̂̂肠���̏����́A�u����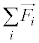 ����x�N�g���ł����Ă��A�͂̃��[�����g�̘a
����x�N�g���ł����Ă��A�͂̃��[�����g�̘a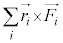 ����x�N�g���v�Ƃ������ƂɂȂ�܂��B
����x�N�g���v�Ƃ������ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
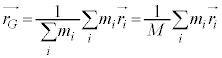 ���A
���A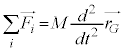 �@����B
�@����B