東北大物理'10年前期[3]
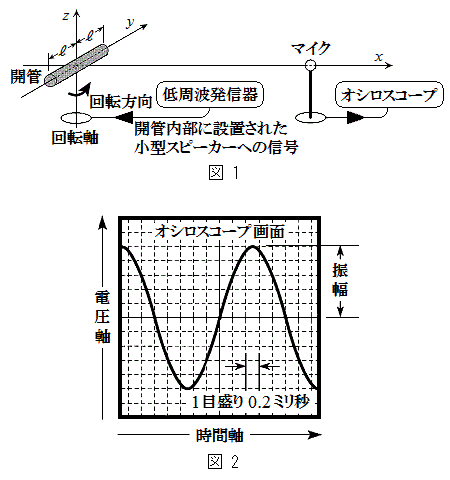 図1に示すような長さ
図1に示すような長さ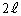 で両端の開いた管(開管)が、z軸上の回転軸に開管の中心が原点と一致するように固定されている。回転軸が矢印の方向に回ることにより、開管はx-y平面内でz軸の正方向から見て反時計回りに回転できる。開管内部には低周波発信器に接続された小型スピーカーが取り付けられている。低周波発信器から適切な振動数の正弦波を小型スピーカーに入力すると、開管内の気柱に両方の開口端が腹の位置となる定常波を作ることができる。定常波を音源とした音は、両方の開口端が出口となり周囲に伝わる。この音の波形は、x-y平面上に置かれたマイクを通してオシロスコープで調べることができる。
で両端の開いた管(開管)が、z軸上の回転軸に開管の中心が原点と一致するように固定されている。回転軸が矢印の方向に回ることにより、開管はx-y平面内でz軸の正方向から見て反時計回りに回転できる。開管内部には低周波発信器に接続された小型スピーカーが取り付けられている。低周波発信器から適切な振動数の正弦波を小型スピーカーに入力すると、開管内の気柱に両方の開口端が腹の位置となる定常波を作ることができる。定常波を音源とした音は、両方の開口端が出口となり周囲に伝わる。この音の波形は、x-y平面上に置かれたマイクを通してオシロスコープで調べることができる。
床や壁などは、音が通過および反射をしない材質でできているとして、以下の問いに答えよ。解答は、解答用紙の所定の場所に記入せよ。また、結果だけでなく考え方や計算の過程も記せ。
問(1) 図1のように、開管の中心軸をy軸と一致させて開管を静止させた。低周波発信器の振動数をゼロからゆっくりと増加させていくと、ある振動数になったとき開管内の気柱に基本振動の定常波ができ、開口端から音が響き始めた。この音をx軸上に置かれたマイクを通してオシロスコープで調べた。オシロスコープの時間軸1目盛りの間隔を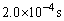 (
(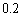 ミリ秒)にしたところ、図2で示すような波形を観測することができた。
ミリ秒)にしたところ、図2で示すような波形を観測することができた。 (a) オシロスコープに表示された波形から、定常波の周期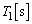 の数値および振動数
の数値および振動数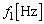 の数値を求めよ。
の数値を求めよ。 (b) 音速が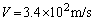 であるとき、図2で観測した音の波長
であるとき、図2で観測した音の波長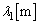 の数値を、有効数字2桁で求めよ。
の数値を、有効数字2桁で求めよ。 (c) 開管内の気柱の固有振動のうち、波長が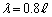 に対応する低周波発信器の振動数
に対応する低周波発信器の振動数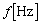 の数値を求めよ。
の数値を求めよ。 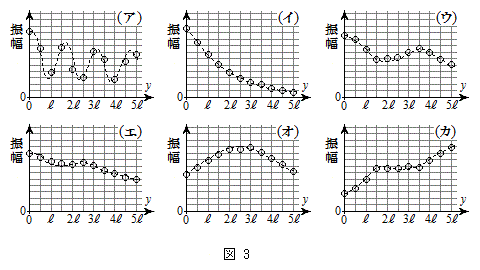 (d) 低周波発信器の振動数をf に固定して、開管内の気柱に作られる定常波の波長を
(d) 低周波発信器の振動数をf に固定して、開管内の気柱に作られる定常波の波長を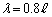 とした。2つの開口端から出た音の干渉を調べるため、マイクを
とした。2つの開口端から出た音の干渉を調べるため、マイクを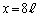 の線上でy軸正方向に移動させた。マイクを通してオシロスコープで測定した振幅とマイクのy座標位置の関係を示す最も適切なグラフを、図3の(ア)〜(カ)の中から1つ選べ。また、そのグラフを選んだ理由を記せ。なお、グラフを見やすくするために、○で示す測定値はなめらかな破線で結んである。
の線上でy軸正方向に移動させた。マイクを通してオシロスコープで測定した振幅とマイクのy座標位置の関係を示す最も適切なグラフを、図3の(ア)〜(カ)の中から1つ選べ。また、そのグラフを選んだ理由を記せ。なお、グラフを見やすくするために、○で示す測定値はなめらかな破線で結んである。
問(2) 次に、低周波発信器の振動数を問(1)(c)で求めたf に固定し、開管を角速度ω で回転させた。このとき、回転による開口端の速度は音速Vより十分に遅く、実験室内には風がない。また、開口端外からの音はないものとする。
(a) 開管の中心軸がy軸と重なるとき、2つの開口端はそれぞれ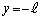 と
と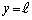 の位置にある。このときの時刻を
の位置にある。このときの時刻を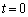 とし、そのとき
とし、そのとき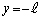 にあった開口端の速度のx成分
にあった開口端の速度のx成分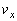 とy成分
とy成分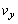 を、
を、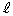 ,ω,t を用いて表せ。
,ω,t を用いて表せ。 (b) マイクを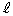 の長さに比べると開管から十分に離れたx軸上の点に移動した。開口端速度のx方向成分
の長さに比べると開管から十分に離れたx軸上の点に移動した。開口端速度のx方向成分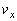 が周期的に変化するため、ドップラー効果により開口端から放出される音の波長もまた周期的に変化する。マイクの位置で観測される音の波長の最小値と最大値を、
が周期的に変化するため、ドップラー効果により開口端から放出される音の波長もまた周期的に変化する。マイクの位置で観測される音の波長の最小値と最大値を、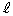 ,ω,Vを用いて求めよ。
,ω,Vを用いて求めよ。 (c) 回転する2つの開口端からの音波には、ドップラー効果による振動数のわずかな違いがあるため、うなりが生ずる。振動数の違いは周期的に変わるので、うなりの回数もまた周期的に変化する。マイクの位置で観測されるうなりの単位時間あたりの回数の最大値を、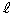 ,ω,Vを用いて表せ。
,ω,Vを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 その昔、1960年代から1970年代にかけて、多くのロック・バンドで使われていたレスリー・スピーカーがネタになっていて、当時、ハモンド・オルガンに酔っていたオールド・ロック・ファンがしびれてしまう問題です。
入試本番間近だというのに、レスリーが泣かせてくれる、ユーライア・ヒープの名曲「7月の朝」を聞きながら数学の難問を考えていた頃が懐かしいですね。
問(1)(a) 図2よりオシロスコープで観測された波形の周期は2ミリ秒です。
定常波の周期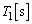 は、
は、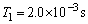 ......[答]振動数
......[答]振動数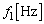 は、
は、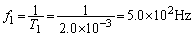 ......[答]
......[答] (b) 波の公式より、波長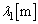 は、
は、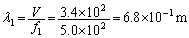 ......[答]
......[答] 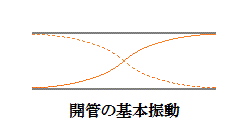 (c) 開管の基本振動の波長は、
(c) 開管の基本振動の波長は、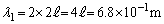
∴ 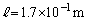
波の公式より、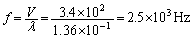 ......[答]注.
......[答]注.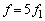 なので
なので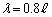 の振動は、5倍振動です。
の振動は、5倍振動です。 (d) まず、きちんと計算してみます。y軸上で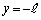 に位置する開口端と、
に位置する開口端と、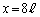 でx軸から距離yの位置との距離
でx軸から距離yの位置との距離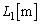 は、
は、 y軸上で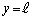 に位置する開口端と、
に位置する開口端と、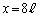 でx軸から距離yの位置との距離
でx軸から距離yの位置との距離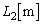 は、
は、 両経路の経路差は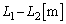 ですが、yを
ですが、yを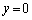 から大きくしていくとき、両開口端から来る音が最初に強めあう条件は、
から大きくしていくとき、両開口端から来る音が最初に強めあう条件は、 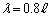 より、
より、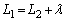 両辺を2乗して、
両辺を2乗して、これより、
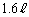 で割って、さらに2乗すると、
で割って、さらに2乗すると、∴ 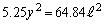 ∴
∴ 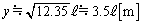
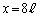 の線上でy軸正方向に移動すると、
の線上でy軸正方向に移動すると、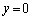 の位置では両音源から等距離にあって強め合うのですが、そこから次第に音の振幅は減少して極小になったのちに増大して、
の位置では両音源から等距離にあって強め合うのですが、そこから次第に音の振幅は減少して極小になったのちに増大して、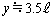 で極大になります。こうなっているグラフは(ウ)です。
で極大になります。こうなっているグラフは(ウ)です。
ここでは、理由を書けばよいので、以下のような概略の近似計算でOKでしょう。(ウ) ......[答]理由:経路差は近似的に、マイク位置のy座標をy,原点とマイクを結ぶ直線とx軸のなす角をθ として、 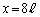 の線上で
の線上で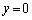 からy軸正方向に移動すると、最初に強め合う条件は、
からy軸正方向に移動すると、最初に強め合う条件は、よって、おおよそ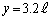 で最初に強めあう。これに最も近いのは(ウ)。 ......[答]
で最初に強めあう。これに最も近いのは(ウ)。 ......[答]
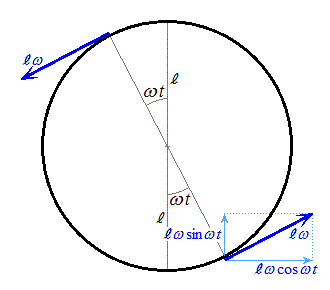 問(2)(a) 右図より、最初に
問(2)(a) 右図より、最初に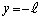 にあった開口端の速度のx成分
にあった開口端の速度のx成分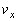 とy成分
とy成分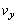 は、
は、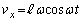 ,
,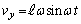 ......[答]
......[答](b) 最初に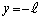 と
と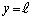 にあった開口端が発する音は半周期ずれて観測されるだけなので、最初に
にあった開口端が発する音は半周期ずれて観測されるだけなので、最初に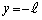 にあった開口端の発する音のドップラー効果を考えれば十分です。
にあった開口端の発する音のドップラー効果を考えれば十分です。 十分に離れたx軸上の点においては開口端から出てくる音が進む速度はx軸方向成分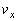 のみ考えればよく、ドップラー効果の公式より、観測される音の振動数
のみ考えればよく、ドップラー効果の公式より、観測される音の振動数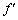 は、
は、 波長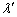 は、
は、 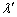 は
は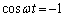 のときに最大で、最大値は、
のときに最大で、最大値は、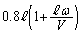 ......[答]
......[答]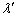 は
は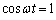 のときに最小で、最小値は、
のときに最小で、最小値は、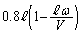 ......[答]
......[答]注.問題文に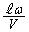 を微小量と考えよ、という指示がついていますが、
を微小量と考えよ、という指示がついていますが、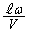 の1次の項を無視すると、ドップラー効果そのものを無視することになってしまいます。
の1次の項を無視すると、ドップラー効果そのものを無視することになってしまいます。 (c) 最初に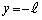 にあった開口端が発する音を観測してドップラー効果による波長が最大となるとき(振動数が最小値
にあった開口端が発する音を観測してドップラー効果による波長が最大となるとき(振動数が最小値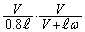 をとるとき)、最初に
をとるとき)、最初に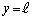 にあった開口端が発する音のドップラー効果による波長が最小(振動数が最大値
にあった開口端が発する音のドップラー効果による波長が最小(振動数が最大値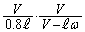 をとる)になります。このときに、両振動数の差が最大となり、単位時間あたりのうなりの回数も最大になります。よって、求める最大値は、
をとる)になります。このときに、両振動数の差が最大となり、単位時間あたりのうなりの回数も最大になります。よって、求める最大値は、 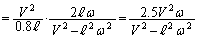
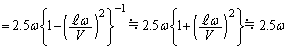 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。