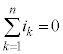�L���q�z�b�t�̖@���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��1�@���F��H���̂���ߓ_�ɗ��������d���̘a�Ɨ��o�����d���̘a�͓������B
��2�@���F��H���̕�H�ɂ����āA�N�d�͂̑��a���d���~���̑��a�͓������B
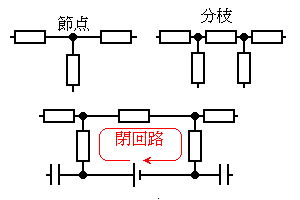 �d�C���i��ڑ����Ăł���܂Ƃ܂����H�ƌ����܂��B��H�̒��œd�C���i�Ɠd�C���i��ڑ����Ă���_���ߓ_�A�ߓ_�Ɛߓ_�̊Ԃ̕�����d�C���i���܂߂����}�ƌ����܂��B
�d�C���i��ڑ����Ăł���܂Ƃ܂����H�ƌ����܂��B��H�̒��œd�C���i�Ɠd�C���i��ڑ����Ă���_���ߓ_�A�ߓ_�Ɛߓ_�̊Ԃ̕�����d�C���i���܂߂����}�ƌ����܂��B
�d�C��H�̒��ŁA���镔�i����o�����ēr��邱�ƂȂ���H�̌��������ǂ��Ă��Ƃ̕��i�ɖ߂��Ă���Ƃ��A���̓���������H�ƌ����܂��B
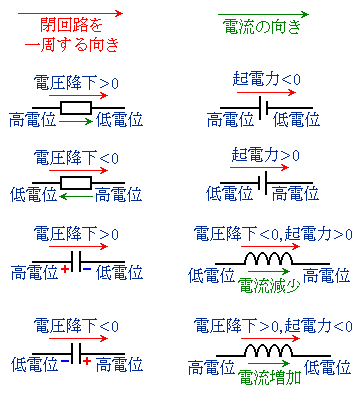 �d�C���i���d���������Ƃ��A�d���͓d�ʂ̍���������Ⴂ���Ɍ������ė���܂��B���}���d���̗��������ɐi�ނƂ��A�����������̓d�ʍ����d���~���܂����d�ʍ~���ƌ����܂��B�d���~�����d�ʂ�������Ƃ��ɐ��ł��B
�d�C���i���d���������Ƃ��A�d���͓d�ʂ̍���������Ⴂ���Ɍ������ė���܂��B���}���d���̗��������ɐi�ނƂ��A�����������̓d�ʍ����d���~���܂����d�ʍ~���ƌ����܂��B�d���~�����d�ʂ�������Ƃ��ɐ��ł��B
�d�r�̂悤�ɁA�d������������\�͂����d�C���i���[���d�����N�d���ƌ����܂��B�N�d�������̂Ƃ��A�d���̗��������ɐi�ނƁA�N�d�͕������d�ʂ��㏸���܂��B
��H������R�ɁA��H�����������d���������Ƃ��A�d���~���͐��ł��B��R�ɁA��H���������Ƌt�������d���������Ƃ��A�d���~���͕��ł��B
�d���~���̐�Βl���I�[���̖@���ɂ���d���̑傫������R�l�����������̂ɂȂ�܂��B
�R���f���T�[�̏ꍇ�́A���d����~���Ă���ɔ����d���ŁA���d����~���Ă���ɔ���d���Ȃ̂ŁA��H�����������A���d����~���Ă���ɔ������d����~���Ă���ɔɌ������Ȃ�A�d���~���͐��ł��B���d����~���Ă���ɔ������d����~���Ă���ɔɌ������Ȃ�A�d���~���͕��ł��B
�R�C���̏ꍇ�́A��H���������ɗ�����d�������������Ƃ��A�����W�������(���Ƃ��d���Ƌt�������d���𗬂����Ƃ���)���N�d�����������܂��B���̂Ƃ��A��H�������������d��������d�ʂ��Ȃ�܂��B������N�d���ƍl����Ȃ����A�d���~���ƍl����Ȃ����ł��B
��H���������ɗ�����d�������������Ƃ��A�����W�������(���Ƃ��d���Ɠ����������d���𗬂����Ƃ���)���N�d�����������A��H������������d���������d���ƂȂ�܂��B������N�d���ƍl����Ȃ����A�d���~���ƍl����Ȃ����ł��B
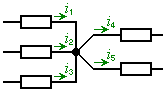 �d�C��H�̒��ł́A�d���͏�������������ĂȂ��Ȃ����肹���ɁA�ǂ��܂łł�����Ă����܂��B�]���āA���镪�}�ɉ����Đߓ_�ɗ��ꍞ���d�����A�ʂ̕��}���炻�̂܂o�čs�����ƂɂȂ�̂���1�@�����������܂��B
�d�C��H�̒��ł́A�d���͏�������������ĂȂ��Ȃ����肹���ɁA�ǂ��܂łł�����Ă����܂��B�]���āA���镪�}�ɉ����Đߓ_�ɗ��ꍞ���d�����A�ʂ̕��}���炻�̂܂o�čs�����ƂɂȂ�̂���1�@�����������܂��B
�Ȃ��A�d��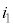 �C
�C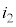 �C
�C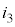 ���ߓ_�ɗ��ꍞ�݁A�d��
���ߓ_�ɗ��ꍞ�݁A�d��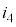 �C
�C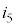 ���ߓ_���痬��o���ꍇ�A
���ߓ_���痬��o���ꍇ�A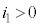 �C
�C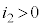 �C
�C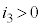 �C
�C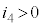 �C
�C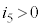 �ƍl����Ƃ��ɂ́A
�ƍl����Ƃ��ɂ́A
�Ƃ������𗧂Ă܂��B
���������d���𐳁A���o�����d���Ƃ��āA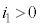 �C
�C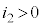 �C
�C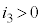 �C
�C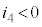 �C
�C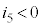 �ƍl����Ƃ��ɂ́A
�ƍl����Ƃ��ɂ́A
�Ƃ������𗧂Ă܂��B
�ߓ_�ɁA�������邢�͗��o�����d��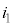 �C
�C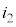 �C����C
�C����C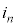 �������āA�d��
�������āA�d��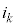 ����������Ƃ���
����������Ƃ���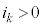 �C���o����Ƃ���
�C���o����Ƃ���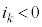 �Ƃ���ꍇ�ɂ́A��1�@�����A
�Ƃ���ꍇ�ɂ́A��1�@�����A
�ƕ\�����Ƃ��ł��܂��B���̏�����������ꍇ�ɂ́A��1�@���́A�u��H���̂���ߓ_�ɗ�������d���̑��a�̓[���v�Ƃ����������ɂȂ�܂��B
����ߓ_����o�����ĕ�H�ɉ����Ĉ������ƁA�r�����d���������Ȃ�����Ⴍ�Ȃ����肵�Ȃ�����Ƃ��d���ɖ߂�A�܂�A�N�d���ǂ����A�d���~���ǂ������������킹��ƁA�o���̘a����v����Ƃ����̂���2�@���ł��B
�L���q�z�b�t��2�@���ł́A��H���������Ƃ��A�e���}���d���~����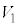 �C
�C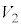 �C����C
�C����C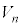 �A�N�d����
�A�N�d����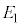 �C
�C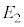 �C����C
�C����C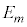 �Ƃ��āA
�Ƃ��āA
�Ƃ������𗧂Ă܂��B
�L���q�z�b�t�̖@����p���ĉ�H�̖��������ꍇ�ɂ́A��1�@���Ƒ�2�@���̎���d���A�d���Ȃǂ̖��m���̌������������āA�A�����������������ƂɂȂ�܂��B
�ǂ̐ߓ_�ɒ��ڂ��邩�A�ǂ̕�H�ɒ��ڂ��邩�A�Ƃ������ƂɍH�v��v��������������܂��B
��2�@���̎����A�l�������H�S�Ăɂ��ď��������ƁA���m���̌������鎮���ł��Ă��܂����Ƃ�����܂����A���̂Ƃ��́A��1�Ǝ�2���玮3�������Ă��܂��A�Ƃ����悤�Ȃ��ƂɂȂ��Ă���̂ł��B���ڂ���ߓ_�A��H�����܂��Ƃ�K�v������܂��B
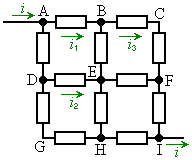 ���@�E�}�̉�H�ŁA��R�͂��ׂ���R�lr�̒�R�A��H�ɗ��ꍞ���d����i�Ƃ��āAA��I�Ԃ�������R�����߂Ă݂܂��B����������H�ł́A���}�̈�����d���̒l��ݒ肹���ɁA��H�̑Ώ̐������܂��������ė������܂��B
���@�E�}�̉�H�ŁA��R�͂��ׂ���R�lr�̒�R�A��H�ɗ��ꍞ���d����i�Ƃ��āAA��I�Ԃ�������R�����߂Ă݂܂��B����������H�ł́A���}�̈�����d���̒l��ݒ肹���ɁA��H�̑Ώ̐������܂��������ė������܂��B
A��B�CA��D�CF��I�CH��I���d���́A��H�̑Ώ̐���蓙�����̂ŁA�����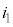 �Ƃ��܂��B
�Ƃ��܂��B
B��E�CD��E�CE��F�CE��H���d�����A��H�̑Ώ̐���蓙�����A�����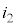 �Ƃ��܂��B
�Ƃ��܂��B
B��C��F�CD��G��H���d�����A��H�̑Ώ̐���蓙�����A�����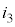 �Ƃ��܂��B
�Ƃ��܂��B
�ߓ_A�ɂ����āA�L���q�z�b�t��1�@�����A
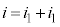 �@����@
�@����@
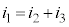 �@����A
�@����A
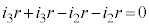 �@����B
�@����B
�@���A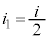
�B���A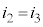
�A�ɑ�����āA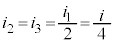
����āAA��B��C��F��I�̓d���́A
A��I�𗬂���d����i�Ȃ̂ŁAA��I��������R�́A�I�[���̖@�����A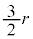 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B