京都大学2002年前期物理入試問題

京都大学2002年前期物理入試問題

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

[1]　次の文を読んで、　　に適した式をそれぞれの解答欄に記入せよ。なお、　　はすでに　　で与えられたものと同じものを表す。

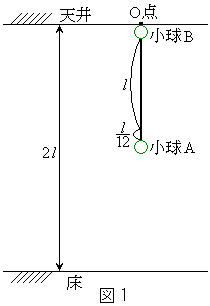
長さlの質量の無視できるゴムひもの両端に、2つの小球AおよびBがついている。小球AおよびBの直径は無視できるほど十分小さく、質量はいずれもmとし、重力加速度をgとする。また、このゴムひもは、引き伸ばされた状態ではフックの法則に基づく復元力が働くが、細くてやわらかいために、たるんだ状態では小球の運動を妨げないものとする。
　図1のように、天井のO点に小球Bを固定し、小球Aを静かにつるしたとき、ゴムひもは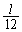

だけ伸びた。このゴムひもが自然長からxだけ引き伸ばされたとき、ゴムひもには

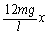の復元力が働く。

(1) 小球Aを小球Bと同じ位置Oまで持ち上げ、小球Bを固定したまま小球Aのみをそのまま自由落下させた。このとき、落下する小球Aが到達する最下端の位置は、天井から　イ　だけ下方となる。小球Aは　イ　の位置から、ゴムひもの復元力　ロ　によって上昇運動をはじめる。その上昇運動において、小球Aは天井からlの位置を速さ　ハ　で通過するが、その瞬間に、天井のO点で固定していた小球Bを静かに解放した。その後、小球AとBは天井から　ニ　の位置で衝突するが、小球Bを解放してから衝突するまでに要する時間は　ホ　である。この衝突が完全非弾性衝突(反発係数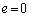

)であり、衝突後は完全にひとつの小球として運動する場合に、衝突してからこの小球が天井から鉛直距離で

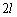だけ下にある床に落下するまでに要する時間は　ヘ　である。

(2) 次に、(1)と同様の手順でO点から小球Aを自由落下させ、　ヘ　の位置に小球Aが到達した瞬間に、O点で固定していた小球Bを静かに解放した。この解放した瞬間においては、小球AとBはゴムひもの復元力　ロ　によって、お互いに引き寄せられている。自由落下している仮想的な観測者からこの2つの小球を見ると、どちらの小球にも重力が働かず、ゴムひもの復元力のみにより運動しているように見える。したがって、小球Bを解放した瞬間からゴムひもが自然長lに戻るまでに要する時間は　ト　であり、その後、小球AとBが衝突するまでにはさらに　チ　だけ時間がかかる。その衝突する位置は天井から　リ　の位置となる。

[解答へ]

[2]　次の文A，Bを読んで、　　に適した式をそれぞれの解答欄に記入せよ。なお、単位系は国際単位系(SI)を用い、すべての装置は真空中に置かれているものとして、真空の透磁率を

とする。

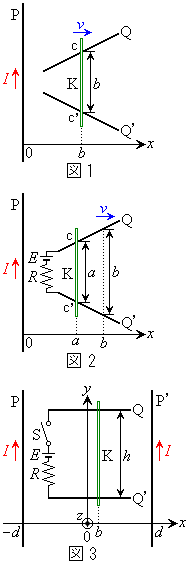
A．図1および図2に示すように、水平面上にある十分に長い直線導体Pに直線電流Iが流れている。2本の直線導体Qおよび

が導体Pを含む水平面内にあり、導体Pから距離xの位置において導体Qと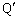

の間隔がxに等しくなるように配置されている。これら2本の導体の上に、質量mの直線導体Kがおかれていて、導体Pと平行のままx方向に摩擦なしに動くことができる。

(1) 図1に示すように、導体Kを一定速度vでx方向に運動させる。導体Kが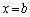

に達したとき、導体Kの位置における磁束密度の大きさは　あ　で与えられ、導体Kが導体Qおよび導体

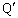と接触する2つの点、cと

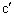の間に発生する起電力は　い　となる。

(2) 図2に示すように、導体Kが位置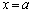

に静止した状態で、導体Qと導体

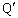の間に抵抗Rを介して起電力Eの電池を接続し、ループ回路を構成する。ただし、導体の抵抗は抵抗Rに比べて十分小さく、また、ループ回路を流れる電流が作る磁界は直線電流Iが作る磁界に比べて十分小さく、いずれも無視できるものとする。このとき、導体Kには大きさ　う　の力が働き、x方向に動き始める。

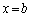に達したときに導体Kの速度がvであったとすると、そのとき導体Kを流れる電流は　え　であり、導体Kの加速度は　お　と表される。そして十分長い時間がたつと、導体Kの速度は一定値　か　に近づいていく。

B．図3に示すように、2本の十分長い直線導体Pおよび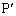

がy軸に平行に

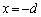および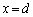

の位置に並んでいて、いずれにもy軸の正の方向の直線電流Iが流れている。これらの導体と同じ平面内にx軸に平行な2本の直線導体Qおよび

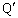が間隔hで並んでいて、導体Qと導体

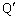の上にはy軸に平行のまま摩擦なしにx軸に沿って動くことのできる質量mの直線導体Kがおかれている。ここでx軸，y軸は水平面内にある。導体Qと導体

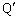の間には、抵抗RとスイッチSを介して起電力Eの電池が接続されており、はじめはスイッチを開いておく。導体の抵抗は抵抗Rに比べて十分小さく、また、ループ回路を流れる電流が作る磁界は電流Iが作る磁界に比べて十分小さく、いずれも無視できるものとする。

(1) 紙面に対して上向きをz軸の正の方向とすると、位置xにおけるz方向の磁束密度は　き　で与えられる。導体Kが原点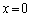

近傍の位置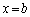

に静止した状態でスイッチSを閉じると、導体Kにはx方向の力　く　が働く。距離bがdに比べて十分短く

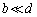が成り立つとき、導体Kに働くx方向の力は　け　と近似することができる。

(2) 初期位置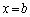

が原点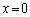

に十分近く、導体Kが磁界中を動くことによって発生する起電力は電池の起電力Eに比べて無視できると仮定する。このとき、導体Kは

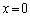の近傍において角振動数ω＝　こ　で単振動する。

(3) 導体Kが磁界中を動くことによって発生する起電力が電池の起電力Eに比べて無視できる条件を求めてみよう。はじめに導体Kが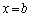

の位置で静止していて、スイッチSを閉じた後

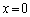のまわりで単振動しているとき、導体Kに発生する起電力の最大値は角振動数ωを用いて　さ　と表される。したがって、この起電力が電池の起電力Eに比べて無視できるための条件は、(2)で求めたωの表式を代入することによって、b≪　し　と表される。

[解答へ]

[3]　次の文を読んで、文中の　　に適した式または数値を、それぞれの解答欄に記入せよ。　　はすでに　　で与えられたものと同じものを表す。なお、微小量x (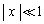

)および実数aに対して成り立つ近似式

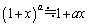を用いよ。

音波と電波の両方を同時に用いると、以下のようにしていろいろな高度での音速を測定することができ、測定された音速から大気の温度の高度分布を知ることができる。ここで音速を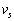

で表し、電波の速さを真空中の光速c (

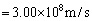)と等しいとする。音速

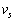は光速cより十分小さいので

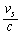は微小量であることに留意せよ。
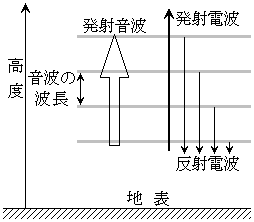
大気は通常では電波を反射しない。しかし、図1に示すように音波を発射して大気の密度の増減を引き起こすと、電波を反射する面が音波の波長に等しい間隔でいく重にもあらわれ、地上から発した電波の一部は、これらの面で反射して再び地上に戻ってくる。この反射面の間隔は音波の振動数を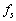

とすると　ア　である。
図1に示すように、地上から垂直に上空に向け、振動数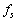

の音波を短時間発した。音波を発して時間

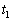後に、音波と同じ方向に、やはり短い時間だけ電波を発射したところ、電波を発して時間

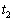後に地上に戻ってきた電波が観測された。このことから反射が生じた高度はh＝　イ　であることがわかる。
電波に対して音波など一般の波と同じようにドップラー効果を考えることができ、観測者および波源の動く速さが光速より十分に小さいときには、ドップラー効果の関係式は音波の場合と同じになる。よって、音速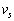

で上昇する仮想的な観測者には電波の振動数は発射した電波の振動数fからずれてみえ、

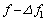と表される。ここで、振動数のずれ

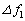は　ウ　となる。したがって、反射してきた電波を地上で測定すると、その振動数は

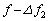と表すことができる。ここで、振動数のずれ

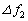は　エ　となり、これより高度hにおける音速を知ることができる。
このような観測では地上に戻る電波が強いことが望ましい。そこで発射する電波の振動数fを変えて繰り返し発射し、反射してくる電波の強度を観測した、その結果、電波の強度は振動数fとともに大きく変化し、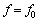

のときに最大になった。その理由を考えてみよう。電波の速さは音速

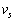で上昇する観測者に対しても光速cに等しいので、振動数fで発射した電波に対して、この観測者が見る波長はλ＝　オ　となる。したがって、異なった反射面で反射される波が互いに強め合う条件は、自然数nを用いてλ＝　カ　となる。この関係式において

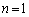とおくと、音速は電波の振動数

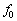を用いて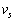

＝　キ　と表すことができる。ただし、

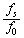は微小量なので

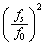を含む項は無視せよ。
音速は高度とともに変化する大気圧には直接依存せず、大気を構成している分子の速さの平均(二乗平均速度)で近似的に与えられることがわかっているので、音速は絶対温度Tの　ク　乗に比例することになる。したがって、いろいろな高度で音速を測定すれば、それぞれの高度における大気の温度を知ることができる。例えば、ある観測の結果、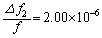

であったとすると、

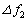が　エ　で与えられることを用いて、電波が反射された高度での音速は　ケ　m/s，温度は　コ　

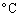となる。それぞれ有効数字3桁および2桁で答えよ。ここで、音速は

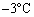において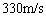

であるとして計算せよ。
[解答へ]

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

　　京大物理TOP　　物理TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。