���s��w2008�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̕���ǂ�ŁA�@�@�ɂ͓K�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�܂���{�@�@}�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł͎w���ɂ��������āA�����ꂼ��̉��ɋL������B
�ȉ��̐ݖ�ł́A���S�͂��ĉ~�^�����镨�̂ɂ��Ė��C�͂ɂ�鑬���̕ω����l����B���̍ہA���܂��܂ȕ����ʂ̔����ȕω��ׂ�B
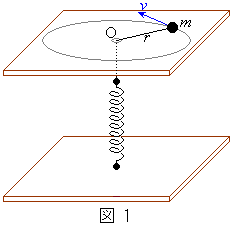
(1) �}1�̂悤�ɁA�Ȃ߂炩�ȑ�̏�ɒu���ꂽ����m�̕��̂��A�Ђ��ɂȂ���Ă���B�Ђ��͑�̒��SO�ɊJ����ꂽ�Ȃ߂炩�ȏ����Ȍ����ђʂ��A�˂ɂȂ���Ă���B����ɂ˂̉��[�͉����̑�ɌŒ肳��Ă���B���̕��͔̂��ar�C����v�̓����~�^�������Ă���B�˒萔��b�ł���A�˂ƂЂ��̎��ʂ͖������Ă悢���̂Ƃ���B�܂��A���̂��_O�ɂ���Ƃ��A�˂̒��������R�̒����ł���悤�ɂȂ��Ă���B
���̓����~�^���ɑ���^����������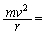 �@�A�@�ƂȂ�B���̂̉^���G�l���M�[��
�@�A�@�ƂȂ�B���̂̉^���G�l���M�[��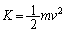 �C�˂̒e���͂̈ʒu�G�l���M�[��
�C�˂̒e���͂̈ʒu�G�l���M�[��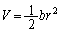 �ŗ^������B���̂Ƃ��^������������^���G�l���M�[K�ƈʒu�G�l���M�[V�̊Ԃ�
�ŗ^������B���̂Ƃ��^������������^���G�l���M�[K�ƈʒu�G�l���M�[V�̊Ԃ�
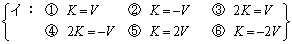
�Ƃ����W�����藧���Ƃ�������B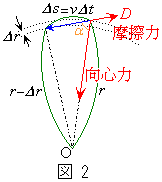
(2) ���ɁA���̕��̂ɑ��x�Ƌt�����ɖ��C�͂���p�����ꍇ���l����B���C�͂̑傫��D�͈��Ƃ���B�˂̗͂ɔ�ׂĔ��ɏ��������C�͂���p�������߁A�}2�̂悤�ɋO�����킸���ɉ~�^������ω������Ƃ��悤�B���̂��߁A���̂̑��x��(1)�ōl�������x�ƌ����ɂ͈قȂ��Ă���B�������A���C�͂����ɏ������ꍇ�ɂ́A���x�̍��͂킸���ł���̂Ŗ������Ă悢���̂Ƃ���B���̂̑�����v�Ƃ���ƁA�}2�̂悤�ɔ����Ȏ���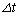 �̊Ԃ̈ړ�������
�̊Ԃ̈ړ�������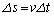 �ŗ^������B���̈ړ��̌��ʁA���̂Ɠ_O�Ƃ̋�����r����
�ŗ^������B���̈ړ��̌��ʁA���̂Ɠ_O�Ƃ̋�����r����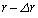 �ɕω�����B���ۂɂ�r�ɔ�ׂĂ��̕ω�
�ɕω�����B���ۂɂ�r�ɔ�ׂĂ��̕ω�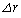 �͔��ɏ��������A���̐}�ł͔����ȕω�
�͔��ɏ��������A���̐}�ł͔����ȕω�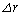 ���������Ă���B�܂��A���̂̉^�������Ƃ˂ɂ����S�͂̊Ԃ̊p�xα��
���������Ă���B�܂��A���̂̉^�������Ƃ˂ɂ����S�͂̊Ԃ̊p�xα��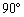 ���킸���ɏ������B
���킸���ɏ������B ���̔����Ȏ���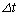 �̊Ԃɐ�����^���G�l���M�[�̔����ȕω�
�̊Ԃɐ�����^���G�l���M�[�̔����ȕω�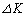 �́A�˂̗͂ɂ��d���Ɩ��C�͂ɂ��d���Ō��܂�̂ŁA
�́A�˂̗͂ɂ��d���Ɩ��C�͂ɂ��d���Ō��܂�̂ŁA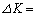 (�@�E�@)�~
(�@�E�@)�~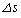 �Ɨ^������B
�Ɨ^������B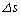 ��
��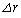 �������ł��邱�Ƃ��A
�������ł��邱�Ƃ��A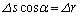 �����藧�Ƃ���B�^���G�l���M�[�̔����ȕω�
�����藧�Ƃ���B�^���G�l���M�[�̔����ȕω�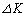 �̂����A�˂ɂ��d���́A���a�̔����ȕω�
�̂����A�˂ɂ��d���́A���a�̔����ȕω�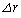 �ɔ�Ⴗ��`���@�G�@�ƕ\�����B���̂˂ɂ��d���ƈʒu�G�l���M�[�̔����ȕω��̊W�ׂ悤�B�O���̔��a��r����
�ɔ�Ⴗ��`���@�G�@�ƕ\�����B���̂˂ɂ��d���ƈʒu�G�l���M�[�̔����ȕω��̊W�ׂ悤�B�O���̔��a��r����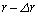 �ɔ����ɕω�����ԂɁA�ʒu�G�l���M�[��
�ɔ����ɕω�����ԂɁA�ʒu�G�l���M�[�� ���������ɕω�����B�㎮�̍Ō�̍s�ł́A�����ȕω�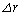 ��2���̍�
��2���̍�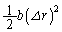 �����Ă���B���̂悤�ɁA�{���ł͔����ȕω���2���̍��͖������Ă悢�B���������ĉ^���G�l���M�[�̔����ȕω��̂����A�˂ɂ��d���̕�����{�I�F�@�@�{1�C�@�A�@�|1�C�@�B�@�{
�����Ă���B���̂悤�ɁA�{���ł͔����ȕω���2���̍��͖������Ă悢�B���������ĉ^���G�l���M�[�̔����ȕω��̂����A�˂ɂ��d���̕�����{�I�F�@�@�{1�C�@�A�@�|1�C�@�B�@�{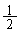 �C�@�C�@�|
�C�@�C�@�|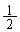 }
}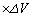 �ƂȂ�B�܂����C�͂ɂ��d���́A�����Ȏ���
�ƂȂ�B�܂����C�͂ɂ��d���́A�����Ȏ���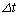 �ɔ�Ⴗ��`���@�J�@�ƕ\�����Ƃ��ł���B���������āA
�ɔ�Ⴗ��`���@�J�@�ƕ\�����Ƃ��ł���B���������āA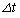 �̊Ԃɐ�����͊w�I�G�l���M�[
�̊Ԃɐ�����͊w�I�G�l���M�[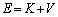 �̔����ȕω�
�̔����ȕω�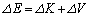 ��
�� 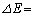 �@�J�@�@�@�@(i)
�@�J�@�@�@�@(i)�Ɨ^������B
���C�͂����ɏ������̂ŁA���̂͋ߎ��I�ɉ~�^����ۂ��Ȃ���A�����������Ɣ��a���ω����Ă����Ƃ���B���̂Ƃ��W���@�C�@�͐��藧���Ă���ƍl���Ă悢�B���������āA�����ȕω�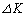 �C
�C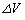 �ɂ��Ă��A�����W��ۂ��Ȃ���A�͊w�I�G�l���M�[��
�ɂ��Ă��A�����W��ۂ��Ȃ���A�͊w�I�G�l���M�[��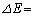 �@�J�@�Ɣ����ɕω����Ă����̂ŁA�^���G�l���M�[�̔����ȕω���
�@�J�@�Ɣ����ɕω����Ă����̂ŁA�^���G�l���M�[�̔����ȕω��� 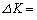 �@�L�@�~(�@�J�@)�@�@�@(ii)
�@�L�@�~(�@�J�@)�@�@�@(ii)�ƂȂ�B(���F�@�L�@�ɂ͓K�Ȑ��l�����Ȃ����B)
(3) ���(2)�ł͔����Ȏ���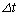 �̊Ԃ̉^���G�l���M�[�̔����ȕω������߂��B���̊ԂɁA���̂̑�����v����
�̊Ԃ̉^���G�l���M�[�̔����ȕω������߂��B���̊ԂɁA���̂̑�����v����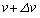 �ɕω�����̂ŁA�^���G�l���M�[�̔����ȕω���
�ɕω�����̂ŁA�^���G�l���M�[�̔����ȕω���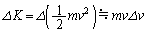 �Ƃ��\����B���̎��Ǝ�(ii)���A���̂̑���v�̕ω�����
�Ƃ��\����B���̎��Ǝ�(ii)���A���̂̑���v�̕ω����� 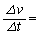 �@�N�@�@�@�@(iii)
�@�N�@�@�@�@(iii)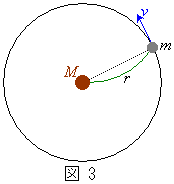
(4) ����܂ł́A���̂��˂̗͂Ə��������C�͂��ċߎ��I�ɉ~�^������ꍇ���l���Ă����B���x�́A�}3�̂悤�ɁA����M�̒n���̎�����^�����鎿��m�̐l�H�q���ɂ��āA����܂łƓ����悤�Ȍv�Z���s���B�n���̒��S����l�H�q���܂ł̋�����r�Ƃ���B�l�H�q���ɂ͒n������̖��L���͂ƁA��C����鏬������C��R�͂���p���Ă���B�������A�l�H�q���̎���m�͒n���̎���M�ɔ�ׂĔ��ɏ��������ߒn���͓����Ȃ��Ƃ��Ă悢�B����ɁA�n���Ɛl�H�q���̑傫���͖������Ă悢���̂Ƃ���B
�܂��A��C�̒�R�͂��͂��炢�Ă��Ȃ��Ƃ���B�l�H�q���͑���v�C���ar�̓����~�^�������Ă���B���L���͒萔��G�Ƃ���Ɖ^����������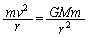 �ƂȂ�B�܂��A���L���͂ɂ��ʒu�G�l���M�[��
�ƂȂ�B�܂��A���L���͂ɂ��ʒu�G�l���M�[��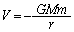 �ł��邱�Ƃ��m���Ă���B���̂Ƃ��^������������A�^���G�l���M�[K�ƈʒu�G�l���M�[V�̊Ԃ̊W��
�ł��邱�Ƃ��m���Ă���B���̂Ƃ��^������������A�^���G�l���M�[K�ƈʒu�G�l���M�[V�̊Ԃ̊W��
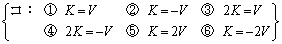
��������B
���ɁA(2)�C(3)�ɂ����門�C�͂Ɠ��l�ɐl�H�q���ɋ�C�̒�R�͂���p�����ꍇ���l����B�����ŋ�C�̒�R�͂́A���x�Ƌt�����ɂ͂��炭�A�傫��D�̈��̗͂Ƃ��Ď�舵���B�������A��C�̒�R�͔͂��ɏ������A�l�H�q���͋ߎ��I�ɉ~�^�����Ă���Ƃ݂Ȃ��Ă悢���̂Ƃ���B
��1�@�l�H�q���̏ꍇ�ɂ��A(2)�Ɠ��l�ɁA�^���G�l���M�[�̔����ȕω�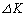 �͖��L���͂Ƌ�C�̒�R�͂ɂ��d���ŗ^������B���̂��Ƃ���A�l�H�q���̗͊w�I�G�l���M�[�̔����ȕω�
�͖��L���͂Ƌ�C�̒�R�͂ɂ��d���ŗ^������B���̂��Ƃ���A�l�H�q���̗͊w�I�G�l���M�[�̔����ȕω�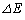 �ɑ��Ď�(i)�����藧���Ƃ��A�v�Z�ߒ����܂߂Ď����Ȃ����B�������A���a��r����
�ɑ��Ď�(i)�����藧���Ƃ��A�v�Z�ߒ����܂߂Ď����Ȃ����B�������A���a��r����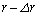 �ɕω�����Ƃ��A�ʒu�G�l���M�[
�ɕω�����Ƃ��A�ʒu�G�l���M�[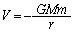 �̔����ȕω���
�̔����ȕω��� �Ƃ����ߎ����ŗ^������B
��2�@��̖�1�̌��ʂƁA�����ȕω�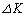 �C
�C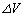 �ɑ��Ă��W���@�R�@�Ɠ����W�����藧���Ƃ�p���āA��(iii)�ɑΉ�����l�H�q���̑���v�̕ω�����\�����������v�Z�ߒ����܂߂ē����Ȃ����B�܂���R�͂ɂ��A�l�H�q������������邩�A��������邩�A�ω����Ȃ����A������ł��邩���A���̗��R�ƂƂ��ɓ����Ȃ����B
�ɑ��Ă��W���@�R�@�Ɠ����W�����藧���Ƃ�p���āA��(iii)�ɑΉ�����l�H�q���̑���v�̕ω�����\�����������v�Z�ߒ����܂߂ē����Ȃ����B�܂���R�͂ɂ��A�l�H�q������������邩�A��������邩�A�ω����Ȃ����A������ł��邩���A���̗��R�ƂƂ��ɓ����Ȃ����B [��]
[2]�@���̕���ǂ�ŁA�@�@�ɂ͓K�������܂��͐��l���A�@�@�ɂ͓K�ȃO���t���A{�@�@}����͓K�Ȃ��̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ�������\���B�܂��A��1�C��2�ł͎w���ɂ��������āA�����ꂼ��̉��ɋL������B
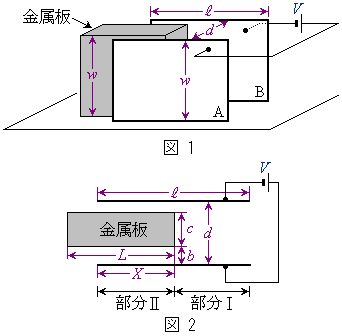
�}2�̂悤�ɁA��w�C����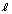 �̒����`��2���̋ɔ�A�CB���Ԋud�Ō��������킹�ɔz�u���ꂽ���s�R���f���T�[���l����B�s����(�≏��)�ō��ꂽ�����łȂ߂炩�ȑ�̏�ɋɔ�A�CB�͌Œ肳��Ă���A���̊Ԃɂ��炩���ߑѓd���Ă��Ȃ���w�̒����̂̋������ɔ�A�CB�ƐڐG���Ȃ��悤�ɑ}������Ă���B�����͂��ׂĕs���̂̋C�̒��ɂ���A���̋C�̗̂U�d����ε�Ƃ���B�ɔ͐}1�̂悤�ɋN�d��V�̓d�r�Ɛڑ�����Ă���B
�̒����`��2���̋ɔ�A�CB���Ԋud�Ō��������킹�ɔz�u���ꂽ���s�R���f���T�[���l����B�s����(�≏��)�ō��ꂽ�����łȂ߂炩�ȑ�̏�ɋɔ�A�CB�͌Œ肳��Ă���A���̊Ԃɂ��炩���ߑѓd���Ă��Ȃ���w�̒����̂̋������ɔ�A�CB�ƐڐG���Ȃ��悤�ɑ}������Ă���B�����͂��ׂĕs���̂̋C�̒��ɂ���A���̋C�̗̂U�d����ε�Ƃ���B�ɔ͐}1�̂悤�ɋN�d��V�̓d�r�Ɛڑ�����Ă���B
�}2�͐}1���̏�����猩�����̂ł���B�����͌���c�C����L�ł���A�ɔɕ��s�ɋɔ�A���狗��b����A�R���f���T�[�̍��[���璷��X�����}������Ă���B�����Ő}2�̉E���Ɏ����悤��x���Cy�����`���A�}2�̉E������x�̐������A�������y�̐������Ƃ���B�ȉ��ł́A�ɔƋ����̒[�ɂ�����d��(�d�E)�̗���͖����ł��A�d��͑S��y�̐������݂̂������Ă���Ƃ���B
���̃R���f���T�[�́A�}2�Ɂu�����T�v�Ƃ��ċɔԂɋ��������݂��Ȃ������ƁA�u�����U�v�Ƃ��Ď������ɔԂɋ��������݂��镔����2�̕���R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B���̃R���f���T�[�ɒ~����ꂽ�G�l���M�[���@�C�@�ł���B
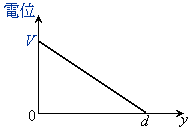
���̃R���f���T�[�̕����T�ɂ���y�̐������̓d�ʂ̕ω����O���t�ɕ\���ƁA�}3�̂悤�ɂȂ�B�}3�ł́A�ɔ�A����̋���������y�ɂƂ�A�ɔ�B�̓d�ʂ�0�Ƃ����B���̐}���Q�l�ɁA�����U�ɂ���y�̐������̓d�ʂ̕ω����O���t�ɕ\�����@���@�̂悤�ɂȂ�B(�O���t�ɂ�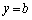 �ł̓d�ʂ����ŋL������B)
�ł̓d�ʂ����ŋL������B)
���̃R���f���T�[�̕����T�ɒ~����ꂽ�G�l���M�[���T�̋ɔԂ̓d��̋���E��p���ĕ\���ƁA�@�n�@�~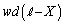 �ƂȂ�B
�ƂȂ�B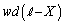 �͕����T�̋ɔԂ̋�Ԃ̑̐ςł��邩��A���̋�Ԃɂ͒P�ʑ̐ς������@�n�@�̃G�l���M�[���~�����Ă���ƍl���邱�Ƃ��ł���B���̂悤�ɍl�����ꍇ�A�����U�̋ɔԂ̋������ɒ~����P�ʑ̐ς�����̃G�l���M�[���@�j�@�ƂȂ�B
�͕����T�̋ɔԂ̋�Ԃ̑̐ςł��邩��A���̋�Ԃɂ͒P�ʑ̐ς������@�n�@�̃G�l���M�[���~�����Ă���ƍl���邱�Ƃ��ł���B���̂悤�ɍl�����ꍇ�A�����U�̋ɔԂ̋������ɒ~����P�ʑ̐ς�����̃G�l���M�[���@�j�@�ƂȂ�B
�Ƃ���ŁA�}2�̋����ɂ͐Ód�C�͂��͂��炭���Ƃ��킩���Ă���B���̂��Ƃ����̂悤�ɒ��ׂĂ݂悤�B�����ŁA�d�r�̓�����R�A�d�r�ƃR���f���T�[�̊Ԃ̔z���̓d�C��R�A���������̓d�C��R�A�����Ƒ�̊Ԃ̖��C�͂�����������ł�����̂Ƃ���B
�܂��A�����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����ɂ��čl���悤�B�Ód�C�͂�x���ɕ��s�Ȑ����ɂ肠���O�͂������ɉ����A�ɔ�A����̋���b��ۂ����܂܁A�ɔԂɑ��݂�������̒�����X����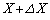 �܂Ŕ����ω��������Ƃ��悤�B���̂Ƃ��̃R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ��@�z�@�ł���B�܂��A���̊Ԃɓd�r�������d�����@�z�@�~�@�w�@�ł���B�R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ���d�r�̂����d�������������̂��A�O�͂������ɂ����d���ɓ������B���̂��Ƃ���A�����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫�������߂���@�z�@���@�g�@�ƂȂ�B�܂��A���̕�����{ �`�F�@�@x�̐������@�A�@x�̕����� }�ł���B
�܂Ŕ����ω��������Ƃ��悤�B���̂Ƃ��̃R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ��@�z�@�ł���B�܂��A���̊Ԃɓd�r�������d�����@�z�@�~�@�w�@�ł���B�R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ���d�r�̂����d�������������̂��A�O�͂������ɂ����d���ɓ������B���̂��Ƃ���A�����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫�������߂���@�z�@���@�g�@�ƂȂ�B�܂��A���̕�����{ �`�F�@�@x�̐������@�A�@x�̕����� }�ł���B
��1�@�����ɂ͂��炭�Ód�C�͂�y���ɕ��s�Ȑ����̑傫���͂����炩�B���̗��R�ƂƂ��ɋL�q����B
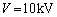 �C
�C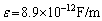 �C
�C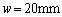 �C
�C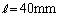 �C
�C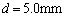 �̂Ƃ��A
�̂Ƃ��A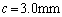 �C
�C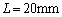 �̋�����
�̋�����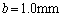 �Ƃ��ċɔԂ�
�Ƃ��ċɔԂ�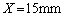 �}�������B���̂Ƃ��ɋ����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫����L������2�����ŋ��߂�ƁA�@���@ N�ƂȂ�B
�}�������B���̂Ƃ��ɋ����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫����L������2�����ŋ��߂�ƁA�@���@ N�ƂȂ�B
��2�@�}2�̋����̑���ɁA�O�`�͂܂����������ł��̓������ɂȂ��Ă�����������ɔԂɑ}�����邱�Ƃɂ���B�܂��A���̋��ɂ͗U�d��ε�̕s���̂̋C�̂������Ă���Ƃ���B���̋������ɂ͂��炭�Ód�C�͂�x�������y���ɕ��s�Ȑ����́A�}2�̋�����p�����Ƃ��ɔ�ׁA���ꂼ��ǂ��ω����邩�B���̗��R�ƂƂ��ɋL�q����B [��]
[3]�@���̕���ǂ�ŁA�@�@�ɂ͓K�������܂��͐��l���A{�@�@}�ɂ͐}3����K�Ȃ��̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B�܂��A��1�C��2�ł͎w���ɂ��������āA�����ꂼ��̉��ɋL������B
�d���g�̈��ł�������̕��˂Ƒ���ɂ��čl�@���悤�B�������\�����錴�q�͓d�q�ƌ��q�j����Ȃ�A���q�j�̓����̃G�l���M�[��������Ԃ���Ⴂ��ԂɈڂ�Ƃ��ɁA���q�j������������˂����B�ȉ��ł́A�d�q�̎��ʂ͌��q�j�̎��ʂƔ�r���Ĕ��ɏ��������߁A�����ł�����̂Ƃ���B
�U����f�̓d���g�́A������̃G�l���M�[�����������q�̏W�܂�ƍl���邱�Ƃ��ł��A���̗��q�����q�Ƃ����B���q1�̃G�l���M�[��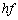 �C�^���ʂ͓d���g�̐i�ތ�����
�C�^���ʂ͓d���g�̐i�ތ�����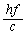 �̑傫���ł��邱�Ƃ��킩���Ă���B�����ŁAh�̓v�����N�萔�Ƃ���萔�ł���Ac�͌����ł���B
�̑傫���ł��邱�Ƃ��킩���Ă���B�����ŁAh�̓v�����N�萔�Ƃ���萔�ł���Ac�͌����ł���B
�ȉ��ɂ����āA���q�j�̓����̃G�l���M�[��Ԃɂ́A��N��ԂƂ���G�l���M�[�̍�����ԂƊ���ԂƂ���G�l���M�[�̍ł��Ⴂ��Ԃ�2��������̂Ƃ���B��N��Ԃ̃G�l���M�[��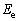 �C����Ԃ̃G�l���M�[��
�C����Ԃ̃G�l���M�[��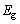 �Ƃ��A���̃G�l���M�[����
�Ƃ��A���̃G�l���M�[����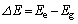 �Ƃ���B
�Ƃ���B
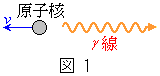 �܂��A����M�̌��q�j1�ɂ��������˂��l����B���q�j����N��Ԃ������ԂɈڂ�Ƃ��ɁA�����̌��q��1���˂����B�Î~���Ă������q�j�́A�}1�̂悤�Ƀ������˂̔���p�ɂ�葬��v�œ����o���B����v�̌��q�j�̉^���G�l���M�[�Ɖ^���ʂ̑傫���́A���q�j������Ԃɂ��邩��N��Ԃɂ��邩�Ɋւ��Ȃ��A���ꂼ��
�܂��A����M�̌��q�j1�ɂ��������˂��l����B���q�j����N��Ԃ������ԂɈڂ�Ƃ��ɁA�����̌��q��1���˂����B�Î~���Ă������q�j�́A�}1�̂悤�Ƀ������˂̔���p�ɂ�葬��v�œ����o���B����v�̌��q�j�̉^���G�l���M�[�Ɖ^���ʂ̑傫���́A���q�j������Ԃɂ��邩��N��Ԃɂ��邩�Ɋւ��Ȃ��A���ꂼ��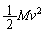 �C
�C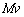 �Ƃ��Ă悢�B�܂��A���q�j�̑S�G�l���M�[�͓����̃G�l���M�[(
�Ƃ��Ă悢�B�܂��A���q�j�̑S�G�l���M�[�͓����̃G�l���M�[(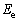 �܂���
�܂���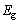 )�ƌ��q�j�̉^���G�l���M�[�̘a�ŗ^������B����Č��q�j����U����
)�ƌ��q�j�̉^���G�l���M�[�̘a�ŗ^������B����Č��q�j����U����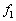 �̃��������˂����ꍇ�A�G�l���M�[�ۑ�����
�̃��������˂����ꍇ�A�G�l���M�[�ۑ�����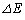 ��p�����@���@�C�^���ʕۑ������@���@�Ə������Ƃ��ł���B�����ŁA
��p�����@���@�C�^���ʕۑ������@���@�Ə������Ƃ��ł���B�����ŁA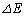 ��
��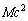 �ɔ�[���ɏ��������Ƃ��킩���Ă���B��Βl��1���[���ɏ�������δ �ɑ��Đ��藧�ߎ���
�ɔ�[���ɏ��������Ƃ��킩���Ă���B��Βl��1���[���ɏ�������δ �ɑ��Đ��藧�ߎ���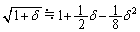 ��p����ƁA
��p����ƁA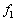 ��
��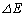 �CM�Cc�Ch��p�����@���@�ƂȂ�B
�CM�Cc�Ch��p�����@���@�ƂȂ�B
���ɁA���̌��q�j�������qN�ō\������Ă���Î~������������̃������q1�̕��˂��l����B���̌����̎��ʂ�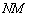 �ŗ^������B�ȉ��ł́A�����͏[���ቷ�ł�����̂Ƃ��A���q�j���������ɌŒ肳��A��������˂��錴�q�j�͂��̔���p���Ă��������ɌŒ肳�ꂽ�܂܂ł���Ƃ���B���̏ꍇ�A�������˂̔���p�͌����S�̂Ŏ~�߂��A����������
�ŗ^������B�ȉ��ł́A�����͏[���ቷ�ł�����̂Ƃ��A���q�j���������ɌŒ肳��A��������˂��錴�q�j�͂��̔���p���Ă��������ɌŒ肳�ꂽ�܂܂ł���Ƃ���B���̏ꍇ�A�������˂̔���p�͌����S�̂Ŏ~�߂��A����������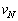 �œ����o�����̂Ƃ���B���̂Ƃ��̕��˃����̐U����
�œ����o�����̂Ƃ���B���̂Ƃ��̕��˃����̐U����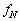 ��
��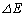 �CM�CN�Cc�Ch��p�����@���@�ƂȂ�B�܂��A�\�����錴�q����������Ƃ݂Ȃ���傫�������̏ꍇ�A���˂��������̐U������
�CM�CN�Cc�Ch��p�����@���@�ƂȂ�B�܂��A�\�����錴�q����������Ƃ݂Ȃ���傫�������̏ꍇ�A���˂��������̐U������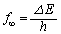 �ƂȂ�B
�ƂȂ�B
��1�@���qN�ō\������Ă���Î~������������̃������q1�̕��˂ɂ��āA�G�l���M�[�ۑ����Ɖ^���ʕۑ������L�q����B�����N��������Ƃ݂Ȃ���Ƃ��A�G�l���M�[�ۑ����ɂ����Č����̉^���G�l���M�[�̍������̑��̍��ɔ�ׂĖ����ł��A���̌��ʁA���˃����̐U������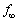 �ƂȂ邱�Ƃ��������B
�ƂȂ邱�Ƃ��������B
���l�̍l�@�ɂ��A������ނ̌��q�ō\������Ă���Î~�����傫�������Ƀ����Ă�ƁA���̌����͐U����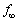 �̃����݂̂��悭�z�����邱�Ƃ��킩���Ă���B���̂悤�Ȍ����������ł͋z���̂Ƃ�ԁB
�̃����݂̂��悭�z�����邱�Ƃ��킩���Ă���B���̂悤�Ȍ����������ł͋z���̂Ƃ�ԁB
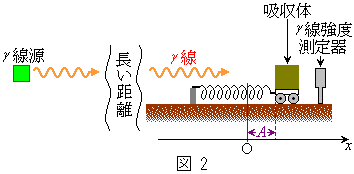
���ɁA�}2�̂悤�Ȏ������u��p���������̑�����l���悤�B
�������͓�����ނ�N�̌��q�ō\�����ꂽ������������Ȃ�A�U����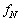 �̃��������̋��x(�P�ʎ��ԓ�����ɕ��˂��������̌��q��)�ŕ��˂�����̂Ƃ���B�z���̂��悹����Ԃ𐅕��ȏ��̏�ɂ����A�}2�̂悤�ɍ��[�����ɌŒ肵���˂ɂȂ��B�������͑�Ԃ���[���ɉ����ɒu����A�����͋z���̕t�߂Ő}2��x���ɕ��s�ɐi�ނ��̂Ƃ���B�z���̂̕\�ʂ�x���ɐ����ł���B�z���̂́A�U����
�̃��������̋��x(�P�ʎ��ԓ�����ɕ��˂��������̌��q��)�ŕ��˂�����̂Ƃ���B�z���̂��悹����Ԃ𐅕��ȏ��̏�ɂ����A�}2�̂悤�ɍ��[�����ɌŒ肵���˂ɂȂ��B�������͑�Ԃ���[���ɉ����ɒu����A�����͋z���̕t�߂Ő}2��x���ɕ��s�ɐi�ނ��̂Ƃ���B�z���̂̕\�ʂ�x���ɐ����ł���B�z���̂́A�U����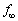 �ȊO�̐U�����̃�����ʉ߂����邪�A�U����
�ȊO�̐U�����̃�����ʉ߂����邪�A�U����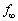 �̃��������S�ɋz��������̂Ƃ���B�z���̂̌���̏���Ƀ������x������ݒu����B�z���̂���̃������˂͖����ł�����̂Ƃ���B
�̃��������S�ɋz��������̂Ƃ���B�z���̂̌���̏���Ƀ������x������ݒu����B�z���̂���̃������˂͖����ł�����̂Ƃ���B
�˂����R�̒����̂Ƃ��̈ʒuO����A�����L���āA����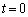 �ɐÂ��ɕ����ƁA��Ԃ�x���ɕ��s�Ɋp�U����ω�ŒP�U������B�ȉ��ł́A�z���̂̉^���ɂ��A�z���̒��Ŋϑ����������̐U����
�ɐÂ��ɕ����ƁA��Ԃ�x���ɕ��s�Ɋp�U����ω�ŒP�U������B�ȉ��ł́A�z���̂̉^���ɂ��A�z���̒��Ŋϑ����������̐U����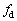 �͉��g�̃h�b�v���[���ʂƓ����ω���������̂Ƃ���B�Ȃ��A�z���̂̋��ܗ��ɂ������̑��x�̕ω��͖����ł�����̂Ƃ���B���̏ꍇ�A�����̔g����λ�Ƃ���ƁA�z���̂�����V�ʼn^�����Ă���Ƃ��́A�Î~���Ă���Ƃ��ɔ�ׁA�P�ʎ��ԓ�����ɋz���̂ɓ��B����g�̐���
�͉��g�̃h�b�v���[���ʂƓ����ω���������̂Ƃ���B�Ȃ��A�z���̂̋��ܗ��ɂ������̑��x�̕ω��͖����ł�����̂Ƃ���B���̏ꍇ�A�����̔g����λ�Ƃ���ƁA�z���̂�����V�ʼn^�����Ă���Ƃ��́A�Î~���Ă���Ƃ��ɔ�ׁA�P�ʎ��ԓ�����ɋz���̂ɓ��B����g�̐���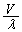 �����ω�����B����āA����t�ɂ�����
�����ω�����B����āA����t�ɂ�����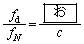 �̊W������B(����λ�CV��p�����ɕ\���B)
�̊W������B(����λ�CV��p�����ɕ\���B)
��Ԃ������n�߂Ă��玞��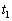 �œˑR�A�����ő��肳���������x���ω������B
�œˑR�A�����ő��肳���������x���ω������B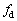 ��
��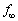 �Ɉ�v��������ł���B��Βl��1���[����������δ �ɑ��Đ��藧�ߎ���
�Ɉ�v��������ł���B��Βl��1���[����������δ �ɑ��Đ��藧�ߎ���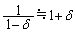 ��p����ƁA
��p����ƁA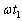 �̖�����������
�̖�����������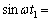 �@���@�ł���B(����
�@���@�ł���B(����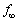 �C
�C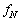 �C
�C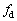 ��p�����ɕ\���B)
��p�����ɕ\���B)
 �����ŁA
�����ŁA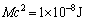 �C
�C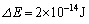 �̌��q�j�̃������˂ɂ����āA
�̌��q�j�̃������˂ɂ����āA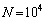 �C
�C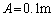 �̂Ƃ���
�̂Ƃ���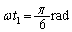 �ő��肳���������x���ω������Ƃ���B�Ȃ��A
�ő��肳���������x���ω������Ƃ���B�Ȃ��A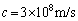 �Ƃ���B���̂Ƃ���ω��L������1�����ŋ��߂���@���@rad/s�ł���B�܂��A��Ԃ�������P�U������Ƃ��A�z�肳���������x��
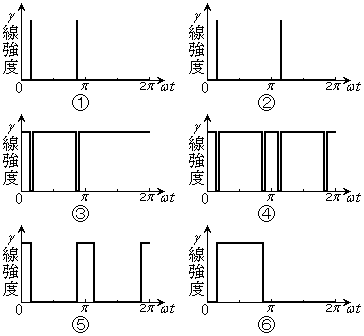
�Ƃ���B���̂Ƃ���ω��L������1�����ŋ��߂���@���@rad/s�ł���B�܂��A��Ԃ�������P�U������Ƃ��A�z�肳���������x��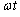 �̊W�͐}3��{�@���@}�̂悤�ɗ\�z�����B
�̊W�͐}3��{�@���@}�̂悤�ɗ\�z�����B
��2�@�}3��{�@���@}��I���������R���L�q����B [��]
�e�⌟��
[1](��������)�@����ꂽ�Ƃ���ɉ��Ă䂯�Γ���͂Ȃ��̂ł����A�ŏI���_���l�Ԃ̏펯�I�Ȋ��o�ƈقȂ�̂ŁA���Ⴂ������A������ŔY�ݍ���ł��܂������Ȗ��ł��B
�o��҂̈Ӑ}�́A�˂̒e���͂̏ꍇ�Ɩ��L���͂̏ꍇ�ƂŁA�e�G�l���M�[�̊W���r���������̂��낤�Ǝv���܂��B
(1)(2)(3)�ł́A�����~�^���̉^������������A�^���G�l���M�[�Ƃ˂̒e���G�l���M�[���������Ȃ邱�ƂɋC�Â����悤�Ƃ��܂��B�˂̒e���G�l���M�[����������Ɠ��ʂ̉^���G�l���M�[���������A���ǁA���C�͂��d��������ƁA�����͌������܂��B
����ɑ�(4)�ł́A�^������������A���L���͂̈ʒu�G�l���M�[���^���G�l���M�[��2�{�ɂ������̂��A�ƁA�킩��̂ł����A���̂Ƃ��ɂ́A��R�͂̂����d���������A�^���G�l���M�[�����債�āA���̂����C�͂ɂ���ĉ��������A�Ƃ����A�펯�A����ςɔ�����悤�Ȍ��ʂ��o�Ă��܂��B
�s�T�̎Γ�����A���ʂ̈قȂ�2���̂𗎉������āA���̗̂��������x�͎��ʂɖ��W�Ƃ����A�����̈�ʏ펯�ɔ����邱�Ƃ��������Ƃ����K�����I�̈�b�̂悤�Ȃ��ƂɂȂ���Ȃ̂ŁA�����ŁA�܂����Ȃ��悤�ɂ��Ȃ�������܂���B
���ʂ���G�l���M�[�����o����͂����Ȃ��A�ƁA�l�Ԃ������狭�ق��Ă��A�����w�́A���q�͔��d���œd�͂������邱�Ƃ����H���Č����Ă���̂ł��B�l�Ԃ͕s���S�ȑ��݂ł��B�_���n�����������w�͐l�Ԃ̊��o������̂ł��B�������ł��A�o�Ă������ʂ��O�Ɏ���Ȃ�������܂���B
���̖��ŏ��X����̂́A�ǂ�������̂����悭�킩��Ȃ��������邱�Ƃł��B(�L)�ɂ��ẮA���l�œ�����A�Ƃ����w�肪���Ă��܂����A(�G)�́u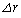 �ɔ�Ⴗ��`�Łv�Ƃ����̂��˘f�����A(�N)���ǂ�������悢�̂��킩��܂���B
�ɔ�Ⴗ��`�Łv�Ƃ����̂��˘f�����A(�N)���ǂ�������悢�̂��킩��܂���B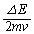 �Ƃ��A
�Ƃ��A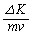 �Ƃ������o�Ă�����ǂ��̓_�����̂ł��傤���H�����̊F����́A�u��(iii)�͒�����̓������x�^���Ɠ����`�����Ă���v�Ƃ�����蕶�̕\�����������������̂��A��ӂ̔c���ɓw�߂Ă��������B
�Ƃ������o�Ă�����ǂ��̓_�����̂ł��傤���H�����̊F����́A�u��(iii)�͒�����̓������x�^���Ɠ����`�����Ă���v�Ƃ�����蕶�̕\�����������������̂��A��ӂ̔c���ɓw�߂Ă��������B
���́A����������[�^�̎����͕s�K���Ǝv���܂��B������A����A���H��̂悤�ɁA���S�L�q���ɂ��ׂ��ł͂Ȃ����A�Ǝv���܂��B
[2](��������)�@�G�l���M�[���x���Ă���_�Ɩ�2�������A�R���f���T�[�̕p�o���ł��B������ł���A��@�ł܂������Ƃ͂Ȃ��͂��ł��B�v�Z�����ʓ|�Ȃ̂Ōv�Z�~�X�ɒ��ӂ��ׂ����ł��傤�B
�R���f���T�[�ɗU�d�̂⓱�̂�}��������ł́A�R���f���T�[��U�d�̂⓱�̂��}������Ă��镔���ƁA�}������Ă��Ȃ������Ƃɕ����āA����E����̍����e�ʂ̌�����p���܂��B
�܂��A�ɔԂ̓d�E�́A���s�R���f���T�[�ł͈�l�Ȃ̂ŁA�ɔԓd��V�C�ɔԂ̓d�EE�C�ɔԋ���d�Ɋւ�������F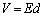 ��p���邱�Ƃ��ł��܂��B
��p���邱�Ƃ��ł��܂��B
�Ód�G�l���M�[U�́A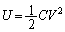 �ł��B�����̊�{�������g�����Ȃ���悤�ɁA�悭���K��ς�ł����Ă��������B
�ł��B�����̊�{�������g�����Ȃ���悤�ɁA�悭���K��ς�ł����Ă��������B
�N�d��V�̓d�r���Ód�e��C�̃R���f���T�[�ɓd��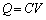 �𑗂荞�ނƂ��ɂ���d��W�́A
�𑗂荞�ނƂ��ɂ���d��W�́A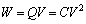 �ł��B�R���f���T�[�����ߍ��ރG�l���M�[��
�ł��B�R���f���T�[�����ߍ��ރG�l���M�[��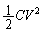 �Ȃ̂ŁA�c���
�Ȃ̂ŁA�c���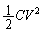 �͉��炩�̕ʂ̎d���Ɏg���܂��B���̖��ł́A���̂��������ގd���Ɏg���܂��B
�͉��炩�̕ʂ̎d���Ɏg���܂��B���̖��ł́A���̂��������ގd���Ɏg���܂��B
��2���������̂�����Ȃ̂��A�ƁA�v�킹�܂����A���̗����������Ȃ̂ł��傤�B
[3](��������)�@���̖��͌��q����̖��̂悤�Ɍ����܂����A��蕶���Ō��q�ɂ��Đ�������Ă��邵�A���q�̃G�l���M�[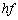 ���A���q�̉^����
���A���q�̉^����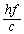 ���^�����Ă���̂ŁA���q����𗚏C���Ă��Ȃ��Ă��ł��܂��B������ő����_���Ȃ��悤�ɒ��ӂ��Ă��������B�O����2���������������ċߎ����邾���Ȃ̂ŁA����͂���܂���B
���^�����Ă���̂ŁA���q����𗚏C���Ă��Ȃ��Ă��ł��܂��B������ő����_���Ȃ��悤�ɒ��ӂ��Ă��������B�O����2���������������ċߎ����邾���Ȃ̂ŁA����͂���܂���B
�㔼�́A�h�b�v���[���ʂɋߎ���������̂ŁA(��)�Ȃǂ��Ȃ��J���邩���m��܂���B�ߎ��̎d�����w�肳��Ă���̂ŁA���Ƃ����āA������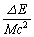 �̌`���Ђ˂�o���Ȃ��Ă͂Ȃ�܂���B(��)���蔲����ꂽ�Ƃ��āA(��)�̃O���t�I���́A�z���̂��������z�����Ă��܂��ƃ������x�����Ƀ������͂��Ȃ��Ȃ邱�Ƃɒ��ӂ��Ă��������B�����������ăO���t��I�����Ă���̂��m�F���邽�߂ɁA��2�ŃO���t�I���̗��R���A�Ƃ����O�̓���悤�ł��B
�̌`���Ђ˂�o���Ȃ��Ă͂Ȃ�܂���B(��)���蔲����ꂽ�Ƃ��āA(��)�̃O���t�I���́A�z���̂��������z�����Ă��܂��ƃ������x�����Ƀ������͂��Ȃ��Ȃ邱�Ƃɒ��ӂ��Ă��������B�����������ăO���t��I�����Ă���̂��m�F���邽�߂ɁA��2�ŃO���t�I���̗��R���A�Ƃ����O�̓���悤�ł��B
[3]�����łȂ��A[1]��[2]�������ł����A���낵����蕶�������ŁA��蕶��ǂ�ł��邾���Ő������Ԃ����Ă��܂��̂ł͂Ȃ����A�ƁA�v����قǂł��B�C�̒Z�������ƁA��蕶��ǂ݂����Ȃ��Ŗ��̈Ӑ}�𐄑����ĉ��l����A�Ƃ����悤�Ȃ��ƂɂȂ肩�˂܂���B����́A���n���ɑ��Ă������lj�͂�v�����Ă���̂ł��B���n���ɕ��w��i��]�_���n�Ǒ��ǂ���A�Ƃ͌����܂��A�u�k�Ђ̃u���[�o�b�N�X�̂����������낻���Ȃ��̂���������Ɠǂݍ���ł����A�Ƃ����悤�Ȃ��Ƃ��炢�͂���Ă����Ē��������Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B