���啨��'08�N�O��[2]
���̕���ǂ�ŁA�@�@�ɂ͓K�������܂��͐��l���A�@�@�ɂ͓K�ȃO���t���A{�@�@}����͓K�Ȃ��̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ�������\���B�܂��A��1�C��2�ł͎w���ɂ��������āA�����ꂼ��̉��ɋL������B
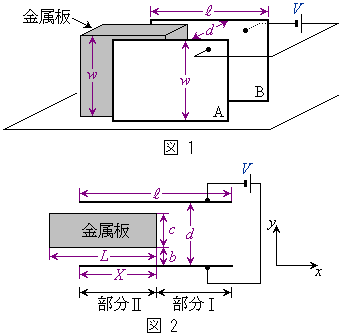
�}2�̂悤�ɁA��w�C���� �̒����`��2���̋ɔ�A�CB���Ԋud�Ō��������킹�ɔz�u���ꂽ���s�R���f���T�[���l����B�s����(�≏��)�ō��ꂽ�����łȂ߂炩�ȑ�̏�ɋɔ�A�CB�͌Œ肳��Ă���A���̊Ԃɂ��炩���ߑѓd���Ă��Ȃ���w�̒����̂̋������ɔ�A�CB�ƐڐG���Ȃ��悤�ɑ}������Ă���B�����͂��ׂĕs���̂̋C�̒��ɂ���A���̋C�̗̂U�d����ε�Ƃ���B�ɔ͐}1�̂悤�ɋN�d��V�̓d�r�Ɛڑ�����Ă���B
�̒����`��2���̋ɔ�A�CB���Ԋud�Ō��������킹�ɔz�u���ꂽ���s�R���f���T�[���l����B�s����(�≏��)�ō��ꂽ�����łȂ߂炩�ȑ�̏�ɋɔ�A�CB�͌Œ肳��Ă���A���̊Ԃɂ��炩���ߑѓd���Ă��Ȃ���w�̒����̂̋������ɔ�A�CB�ƐڐG���Ȃ��悤�ɑ}������Ă���B�����͂��ׂĕs���̂̋C�̒��ɂ���A���̋C�̗̂U�d����ε�Ƃ���B�ɔ͐}1�̂悤�ɋN�d��V�̓d�r�Ɛڑ�����Ă���B
�}2�͐}1���̏�����猩�����̂ł���B�����͌���c�C����L�ł���A�ɔɕ��s�ɋɔ�A���狗��b����A�R���f���T�[�̍��[���璷��X�����}������Ă���B�����Ő}2�̉E���Ɏ����悤��x���Cy�����`���A�}2�̉E������x�̐������A�������y�̐������Ƃ���B�ȉ��ł́A�ɔƋ����̒[�ɂ�����d��(�d�E)�̗���͖����ł��A�d��͑S��y�̐������݂̂������Ă���Ƃ���B
���̃R���f���T�[�́A�}2�Ɂu�����T�v�Ƃ��ċɔԂɋ��������݂��Ȃ������ƁA�u�����U�v�Ƃ��Ď������ɔԂɋ��������݂��镔����2�̕���R���f���T�[�Ƃ݂Ȃ����Ƃ��ł���B���̃R���f���T�[�ɒ~����ꂽ�G�l���M�[���@�C�@�ł���B

���̃R���f���T�[�̕����T�ɂ���y�̐������̓d�ʂ̕ω����O���t�ɕ\���ƁA�}3�̂悤�ɂȂ�B�}3�ł́A�ɔ�A����̋���������y�ɂƂ�A�ɔ�B�̓d�ʂ�0�Ƃ����B���̐}���Q�l�ɁA�����U�ɂ���y�̐������̓d�ʂ̕ω����O���t�ɕ\�����@���@�̂悤�ɂȂ�B(�O���t�ɂ� �ł̓d�ʂ����ŋL������B)
�ł̓d�ʂ����ŋL������B)
���̃R���f���T�[�̕����T�ɒ~����ꂽ�G�l���M�[���T�̋ɔԂ̓d��̋���E��p���ĕ\���ƁA�@�n�@�~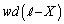 �ƂȂ�B
�ƂȂ�B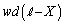 �͕����T�̋ɔԂ̋�Ԃ̑̐ςł��邩��A���̋�Ԃɂ͒P�ʑ̐ς������@�n�@�̃G�l���M�[���~�����Ă���ƍl���邱�Ƃ��ł���B���̂悤�ɍl�����ꍇ�A�����U�̋ɔԂ̋������ɒ~����P�ʑ̐ς�����̃G�l���M�[���@�j�@�ƂȂ�B
�͕����T�̋ɔԂ̋�Ԃ̑̐ςł��邩��A���̋�Ԃɂ͒P�ʑ̐ς������@�n�@�̃G�l���M�[���~�����Ă���ƍl���邱�Ƃ��ł���B���̂悤�ɍl�����ꍇ�A�����U�̋ɔԂ̋������ɒ~����P�ʑ̐ς�����̃G�l���M�[���@�j�@�ƂȂ�B
�Ƃ���ŁA�}2�̋����ɂ͐Ód�C�͂��͂��炭���Ƃ��킩���Ă���B���̂��Ƃ����̂悤�ɒ��ׂĂ݂悤�B�����ŁA�d�r�̓�����R�A�d�r�ƃR���f���T�[�̊Ԃ̔z���̓d�C��R�A���������̓d�C��R�A�����Ƒ�̊Ԃ̖��C�͂�����������ł�����̂Ƃ���B
�܂��A�����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����ɂ��čl���悤�B�Ód�C�͂�x���ɕ��s�Ȑ����ɂ肠���O�͂������ɉ����A�ɔ�A����̋���b��ۂ����܂܁A�ɔԂɑ��݂�������̒�����X����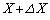 �܂Ŕ����ω��������Ƃ��悤�B���̂Ƃ��̃R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ��@�z�@�ł���B�܂��A���̊Ԃɓd�r�������d�����@�z�@�~�@�w�@�ł���B�R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ���d�r�̂����d�������������̂��A�O�͂������ɂ����d���ɓ������B���̂��Ƃ���A�����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫�������߂���@�z�@���@�g�@�ƂȂ�B�܂��A���̕�����{ �`�F�@�@x�̐������@�A�@x�̕����� }�ł���B
�܂Ŕ����ω��������Ƃ��悤�B���̂Ƃ��̃R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ��@�z�@�ł���B�܂��A���̊Ԃɓd�r�������d�����@�z�@�~�@�w�@�ł���B�R���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω��ʂ���d�r�̂����d�������������̂��A�O�͂������ɂ����d���ɓ������B���̂��Ƃ���A�����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫�������߂���@�z�@���@�g�@�ƂȂ�B�܂��A���̕�����{ �`�F�@�@x�̐������@�A�@x�̕����� }�ł���B
��1�@�����ɂ͂��炭�Ód�C�͂�y���ɕ��s�Ȑ����̑傫���͂����炩�B���̗��R�ƂƂ��ɋL�q����B
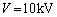 �C
�C �C
�C �C
�C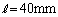 �C
�C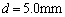 �̂Ƃ��A
�̂Ƃ��A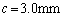 �C
�C �̋�����
�̋�����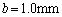 �Ƃ��ċɔԂ�
�Ƃ��ċɔԂ�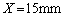 �}�������B���̂Ƃ��ɋ����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫����L������2�����ŋ��߂�ƁA�@���@ N�ƂȂ�B
�}�������B���̂Ƃ��ɋ����ɂ͂��炭�Ód�C�͂�x���ɕ��s�Ȑ����̑傫����L������2�����ŋ��߂�ƁA�@���@ N�ƂȂ�B
��2�@�}2�̋����̑���ɁA�O�`�͂܂����������ł��̓������ɂȂ��Ă�����������ɔԂɑ}�����邱�Ƃɂ���B�܂��A���̋��ɂ͗U�d��ε�̕s���̂̋C�̂������Ă���Ƃ���B���̋������ɂ͂��炭�Ód�C�͂�x�������y���ɕ��s�Ȑ����́A�}2�̋�����p�����Ƃ��ɔ�ׁA���ꂼ��ǂ��ω����邩�B���̗��R�ƂƂ��ɋL�q����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���X�v�Z���ʓ|�ł����A�R���f���T�[�̖��Ƃ��Ă͕W���I�ȃ^�C�v�̖��ł��B
(�C) �����T�̉��������� �C�����T���ʐ���
�C�����T���ʐ���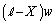 �C�����T���Ód�e����
�C�����T���Ód�e���� �ł��B
�ł��B �����U�͋������}������Ă��܂����A������A����B���ɂł��Ă���2�̃R���f���T�[��ڑ����Ă��邾���ł����āA�Ód�e���ւ̊�^�͂���܂���B�����U���ʐ���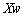 �ł��B������A�Ƃ̊Ԃɂł��Ă���R���f���T�[���Ód�e����
�ł��B������A�Ƃ̊Ԃɂł��Ă���R���f���T�[���Ód�e���� �C������B�Ƃ�������
�C������B�Ƃ������� �ŁA���̕����ɂł��Ă���R���f���T�[���Ód�e����
�ŁA���̕����ɂł��Ă���R���f���T�[���Ód�e����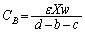 �C
�C ��
��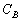 ������ڑ��̍����e��
������ڑ��̍����e��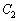 �́A
�́A  ��
�� 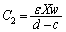
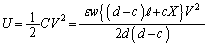 ......[��]
......[��] (��)
(��) 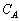 �C
�C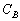 ���[���d����
���[���d���� �C
�C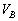 �Ƃ��āA
�Ƃ��āA �C
�C �ɒ~�������d�C���͓������A
�ɒ~�������d�C���͓������A �C
�C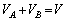 ���A
���A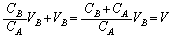 ��
�� 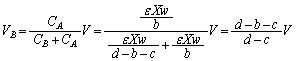
����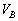 ���A
���A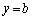 �ł��d��(
�ł��d��( �ɂ������d��)�ɂȂ�܂��B������A (
�ɂ������d��)�ɂȂ�܂��B������A ( )�C������B (
)�C������B (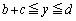 )�̊Ԃ̕����ɂ��ẮA��l���d�E(�d��)���ł��邽�߁A�d�ʂ������ɑ��Ē����I�ɕω����܂�(�d�ʁE�d�����Q��)�B
)�̊Ԃ̕����ɂ��ẮA��l���d�E(�d��)���ł��邽�߁A�d�ʂ������ɑ��Ē����I�ɕω����܂�(�d�ʁE�d�����Q��)�B
��蕶�̃O���t(�}3)�ŁA�ʒuy�ɂ������d����v�Ƃ��āA ��
�� �����Ԓ����̎��́A
�����Ԓ����̎��́A �����ŁA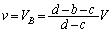 �Ƃ���ƁA
�Ƃ���ƁA ���A
����āA�����U�ɂ�����y�������d���̕ω����O���t�ɕ\���ƁA�E�}�̂悤�ȃO���t�ɂȂ�܂��B (�n) �����T���d�E(�d��)�̋����� �C�Ód�G�l���M�[
�C�Ód�G�l���M�[ �́A
�́A 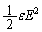 ......[��]
......[��]��蕶���ɂ���悤�ɁA�U�d��ε�̕������[�����Ă����ԓ��Ɉ�l���d�EE������Ƃ��̒P�ʑ̐ϓ�������G�l���M�[(�G�l���M�[���x)�́A �ɂȂ�܂��B
�ɂȂ�܂��B (��) �d��������Ă��Ȃ������̒����d�E(�d��)�͐����܂���B�]���āA�������ɒ~������P�ʑ̐ς�������G�l���M�[�́A0 ......[��]�@�ł��B
(�z) (�C)�̌��ʂɂ����āAX�� �Ƃ���ƁA���̂Ƃ����Ód�G�l���M�[
�Ƃ���ƁA���̂Ƃ����Ód�G�l���M�[ �́A
�́A (�C)�̌��ʂ��������Ƃɂ��A���̊ԂɃR���f���T�[�ɒ~����ꂽ�G�l���M�[�̕ω���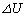 �́A
�́A 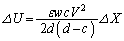 ......[��]
......[��](�w) (�C)�̏��ŃR���f���T�[���~���Ă����d�C����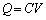 �C
�C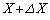 �̂Ƃ��̃R���f���T�[���Ód�e����
�̂Ƃ��̃R���f���T�[���Ód�e���� �Ƃ��āA�R���f���T�[���~���Ă����d�C����
�Ƃ��āA�R���f���T�[���~���Ă����d�C����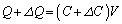 �C
�C X��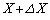 �̊ԂɃR���f���T�[�ɋ������ꂽ�d�C����
�̊ԂɃR���f���T�[�ɋ������ꂽ�d�C���� (�z)�̌��ʂ�
(�z)�̌��ʂ� �Ə�����̂ŁA���̊Ԃɓd�r�����������d���́A
�Ə�����̂ŁA���̊Ԃɓd�r�����������d���́A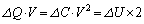 2 ......[��]
2 ......[��] (�g) �d�r�����������d�� �́A�R���f���T�[���Ód�G�l���M�[�̑�����
�́A�R���f���T�[���Ód�G�l���M�[�̑�����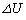 �Ƌ����ɑ��ēd�r�������d���ɂȂ�܂��B�Ƃ������Ƃ́A�d�r�������ɑ��Ă����d����
�Ƌ����ɑ��ēd�r�������d���ɂȂ�܂��B�Ƃ������Ƃ́A�d�r�������ɑ��Ă����d���� �ł�(�R���f���T�[�̉ߓn�������Q��)�B
�ł�(�R���f���T�[�̉ߓn�������Q��)�B �ɔ�A�ɂ����d���A������A�ƑΌ����鑤�ɂ����d�����~�����A�ɔ�B�ɂ����d���A������B�ƑΌ����鑤�ɂ����d�����~������̂ŁA�ɔ�A�CB�Ƌ����̊Ԃɂ͈��͂ƂȂ��Ód�C��(x��������������)�������܂��B
�d�r�������ɂ����d���́A�ɔ�A�CB�Ƌ����Ƃ̊Ԃɓ����Ód�C���������d���ł��B�Ód�C���������d���́A�Ód�C���ɋt�炤�O���������d���Ƀ}�C�i�X���������̂ɂȂ�܂��B�O���̑傫����F�Ƃ��āA�ɔ�A�CB�Ƌ����Ƃ̊Ԃɂ͈��͂������Ă���̂ŁA����ɋt�炤�O���̌�����x���������ł��邱�Ƃ��l�����A�O���������d����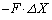 �ł��B�]���āA
�ł��B�]���āA 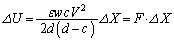 ��
��  �@���(��)
�@���(��)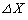 ......[��]
......[��](�`) ��L���A�Ód�C���̌�����x���������ŁA�@ ......[��]
��1�@(�C)�̌��ʂɂ��ƁA�R���f���T�[���Ód�G�l���M�[��X�̊��ł�����y�ɂ͈ˑ������A������y���������������ړ����Ă��Ód�G�l���M�[�͕ω����܂���B����āA�Ód�C����y���ɕ��s�Ȑ����̑傫�� �ɂ��āA
�ɂ��āA
(��) (��)�����A�Ód�C����x���ɕ��s�Ȑ����̑傫���́A
 [N]
[N]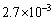 ......[��]
......[��]
��2�@(��)���́A�����̓����`��ɂ͈ˑ������A�\�ʂ������ł��肳������ΐ������܂��B�]���āA�������ɓ����Ód�C����x�������y���ɕ��s�Ȑ����́A�ω����܂���B
�ω����Ȃ��B(�C)�̌��ʂ́A�����ł��������ł��ς��Ȃ�����B ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B