�R���f���T�[�̉ߓn�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(���̍��ڂ̏ڍׂȌv�Z�́A�R���f���T�[�̉ߓn���ۂ̌v�Z���Q��)
�X�C�b�`���������A�R���f���T�[����R�[���̓���(�Z��)�Ƃ��ē��삷��B
�[�d�������́A�R���f���T�[���d���𗬂��Ȃ��B
�Ód�e��C�̃R���f���T�[���[���d����V�ŁA�d��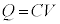 ��~���Ă���Ƃ��A�R���f���T�[���~���Ă����Ód�G�l���M�[U�́A
��~���Ă���Ƃ��A�R���f���T�[���~���Ă����Ód�G�l���M�[U�́A
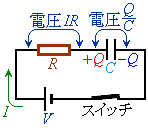 �E�}�̂悤�ɁA�N�d��V�̓d�r����RR���Ód�e��C���R���f���T�[�ƃX�C�b�`��ڑ�������H���l���܂��B�ŏ��ɃR���f���T�[���d����0���Ƃ��܂��B
�E�}�̂悤�ɁA�N�d��V�̓d�r����RR���Ód�e��C���R���f���T�[�ƃX�C�b�`��ڑ�������H���l���܂��B�ŏ��ɃR���f���T�[���d����0���Ƃ��܂��B
�X�C�b�`������Ƃ��ɁA��H�ɗ�����d����I�C�R���f���T�[���~���Ă����d����Q�Ƃ���ƁA��R�ɂ������d���~����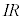 �C�R���f���T�[�ɂ������d���~����
�C�R���f���T�[�ɂ������d���~����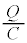 �C�L���q�z�b�t��2�@�����A
�C�L���q�z�b�t��2�@�����A
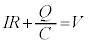 �@����@
�@����@ �X�C�b�`���������A�ŏ��ɃR���f���T�[���d����0�������̂ŁA�@��
�X�C�b�`���������A�ŏ��ɃR���f���T�[���d����0�������̂ŁA�@��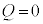 �Ƃ���ƁA
�Ƃ���ƁA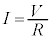 �ƂȂ�܂����A����́A�R���f���T�[����R�[���̓����Œu��������(������Z���ƌ����܂�)�Ƃ����d���ł��B
�ƂȂ�܂����A����́A�R���f���T�[����R�[���̓����Œu��������(������Z���ƌ����܂�)�Ƃ����d���ł��B
���̌�A�R���f���T�[���d�������ꍞ����d��Q�����債�Ă����܂��B
�X�C�b�`������A�[���Ɏ��Ԃ��o��(�ƌ����Ă��ʏ�̓d�C���i���x�̃R���f���T�[���R�ł͂����Ƃ����Ԃł�)���āA�R���f���T�[���d��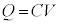 ��~����ƁA�@���A
��~����ƁA�@���A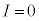 �ƂȂ�A�d��������Ȃ��Ȃ�܂��B�R���f���T�[�̗��ɔԂ͐≏����Ă���̂ŁA�d����~�������Ă��܂��A�d���̗����o�H�͂���܂���B���̏�Ԃ��A�u�R���f���T�[���[�d���ꂽ�v�ƕ\�����܂��B���̏ŁA�R���f���T�[�̗��ɔɂ́A
�ƂȂ�A�d��������Ȃ��Ȃ�܂��B�R���f���T�[�̗��ɔԂ͐≏����Ă���̂ŁA�d����~�������Ă��܂��A�d���̗����o�H�͂���܂���B���̏�Ԃ��A�u�R���f���T�[���[�d���ꂽ�v�ƕ\�����܂��B���̏ŁA�R���f���T�[�̗��ɔɂ́A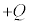 �C
�C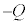 ���d�����~�����Ă��܂��B��R�ɂ��d��������Ă��Ȃ��̂���R���[���d����0�ƂȂ�A�d�r���d���͑S�ăR���f���T�[�ɂ�����܂��B
���d�����~�����Ă��܂��B��R�ɂ��d��������Ă��Ȃ��̂���R���[���d����0�ƂȂ�A�d�r���d���͑S�ăR���f���T�[�ɂ�����܂��B
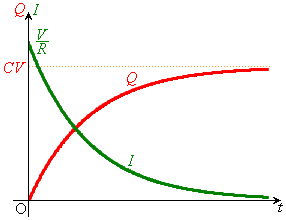
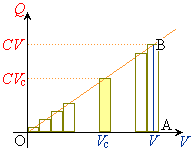
���̊Ԃ́A�d���ƃR���f���T�[���~�����d���̕ω��̏��E�}�Ɏ����܂����B
�����ŁA�R���f���T�[�����߂����Ód�G�l���M�[���l���܂��B
 �R���f���T�[���[���d����
�R���f���T�[���[���d����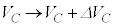 �ƕω�����ԂɁA�R���f���T�[���d����
�ƕω�����ԂɁA�R���f���T�[���d����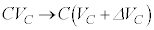 �ƕω����A�d���̕ω�����
�ƕω����A�d���̕ω�����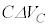 �ł��B
�ł��B
���̊ԂɃR���f���T�[���~�����Ód�G�l���M�[�A�܂�A�R���f���T�[�̎��d���́A�d��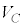 ���d��
���d��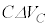 ���ړ�����̂ŁA
���ړ�����̂ŁA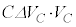 (�d�ʁE�d�����Q��)�ƂȂ�܂��B
(�d�ʁE�d�����Q��)�ƂȂ�܂��B
�d��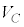 ��0����V�܂ŕω�����Ԃ̏��E�}�Ɏ����܂����B���̒����`�̖ʐς��R���f���T�[�̎��d��
��0����V�܂ŕω�����Ԃ̏��E�}�Ɏ����܂����B���̒����`�̖ʐς��R���f���T�[�̎��d��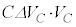 �������Ă��܂��B�����̑��a���R���f���T�[�����߂����Ód�G�l���M�[U�ɂȂ�ƍl�����܂����A
�������Ă��܂��B�����̑��a���R���f���T�[�����߂����Ód�G�l���M�[U�ɂȂ�ƍl�����܂����A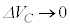 �Ƃ���ƁA�E�}�̎O�p�`OAB�̖ʐ�
�Ƃ���ƁA�E�}�̎O�p�`OAB�̖ʐ�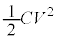 �ɋ߂Â����Ƃ��킩��܂��B����āA�Ód�e��C�̃R���f���T�[���[���d����V�ł���Ƃ��A���̃R���f���T�[�����߂����Ód�G�l���M�[U�́A
�ɋ߂Â����Ƃ��킩��܂��B����āA�Ód�e��C�̃R���f���T�[���[���d����V�ł���Ƃ��A���̃R���f���T�[�����߂����Ód�G�l���M�[U�́A
�R���f���T�[���~���Ă����d��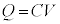 ���l����ƁA�R���f���T�[�����߂����Ód�G�l���M�[��
���l����ƁA�R���f���T�[�����߂����Ód�G�l���M�[��
�ƁA���낢��ɕ\���܂��B
���̊ԁA�d�r�ɂ����ẮA�d��Q�𑗂�o���ԁA�d���͈��lV�ł��B�]���āA�d�r�����������Ód�G�l���M�[�A�܂�A�d�r�̂����d����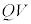 �Ȃ̂ŁA�R���f���T�[�ɂ͔�����
�Ȃ̂ŁA�R���f���T�[�ɂ͔�����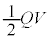 �����~���邱�Ƃ��ł��Ȃ����Ƃ��킩��܂��B�c���
�����~���邱�Ƃ��ł��Ȃ����Ƃ��킩��܂��B�c���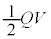 ����R���W���[���M�Ƃ��ď����Ă��܂��܂��B
����R���W���[���M�Ƃ��ď����Ă��܂��܂��B
�������ɂ���ẮA�R���f���T�[�̋ɔԂɓ����������炩���d��������A�Ƃ��������蓾�܂��B�d�r�������d��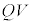 �C����ꂽ�W���[���M���܂߂ċɔԂ��d�C���������d��W�C�R���f���T�[���~�����Ód�G�l���M�[
�C����ꂽ�W���[���M���܂߂ċɔԂ��d�C���������d��W�C�R���f���T�[���~�����Ód�G�l���M�[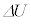 �Ƃ̊Ԃɂ́A�G�l���M�[�ۑ���
�Ƃ̊Ԃɂ́A�G�l���M�[�ۑ���
���������܂��B�������A��蕶�ɂ���ẮA�O���̂����d��W���l����ꍇ������܂��B���̂Ƃ��̃G�l���M�[�ۑ����́A
�Ƃ����`�ɂȂ�܂��B�����d�������Ă���̂��A�Ƃ������Ƃɂ��ĐT�d�ɍl���Ă��������B
�[�d���ꂽ�R���f���T�[�̗��[���łȂ��ƁA�R���f���T�[�̗��ɔɒ~�����Ă���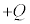 �C
�C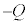 ���d����������ʂ��č��̂��A�R���f���T�[���d����0�ƂȂ�܂��B���̏��u�R���f���T�[�����d���ꂽ�v�ƕ\�����܂��B
���d����������ʂ��č��̂��A�R���f���T�[���d����0�ƂȂ�܂��B���̏��u�R���f���T�[�����d���ꂽ�v�ƕ\�����܂��B
�R���f���T�[�̗��ɔԂɉߑ���d����������ƁA�ɔԂ̐≏��Ԃ��j��ĕ��d���Ă��܂����Ƃ�����܂��B�����Ă��j��Ȃ��ƕۏ���Ă�����E���d�����ϓd���ƌ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B