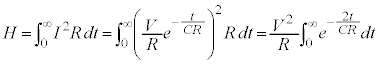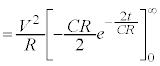コンデンサーの過渡現象の計算 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
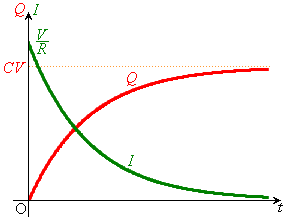
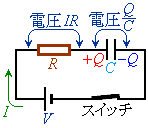右図のように、起電力Vの電池と抵抗Rと静電容量Cのコンデンサーとスイッチを接続した回路を考えます。最初にコンデンサーの電荷は0だとします。
時刻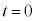
においてスイッチを閉じます。回路に流れる電流をI，コンデンサーが蓄えている電荷をQとすると、抵抗における電圧降下は
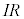，コンデンサーにおける電圧降下は
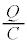，キルヒホッフ第2法則より、
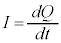より、
積分すると、
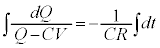(微分方程式を参照)
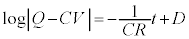(D：積分定数)∴ 
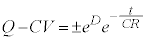はじめにコンデンサーの電荷は0だったので、
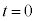において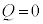
とすると、
∴ 
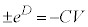
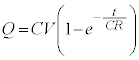
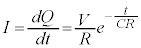
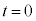のとき、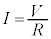
ですが、これは、コンデンサーを抵抗ゼロの導線で置き換えた(これを短絡と言います)ときの電流です。スイッチ投入直後にコンデンサーは短絡されてしまったのと同様の動作をします。
また、充分時間が経過して、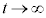
とすると、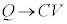
，
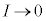となり、コンデンサーの充電が完了しますが、これは、電池を直接コンデンサーに接続した場合と同じ状態になります。電流が流れず抵抗両端の電圧がゼロなので、抵抗はあってもなくても同じことになります。
ここで、コンデンサーが貯めこむ静電エネルギーを考えます。コンデンサー両端の電圧が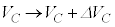
と変化する間に、コンデンサーの電荷は
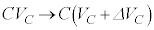と変化し、変化分は
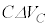です。この間にコンデンサーが蓄えた静電エネルギーは、
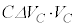(電位ϕの位置における電荷qの静電エネルギーは
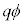，電位を参照)，電圧
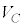が0からVまで変化する間に、コンデンサーが貯めこむ静電エネルギーUは、
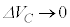として、
最終的な電荷Qについて、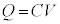
より、コンデンサーが貯めこむ静電エネルギーを
と、いろいろに表せます。
さて、コンデンサーの電圧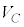
は電荷Qの増大にともなって増大しますが、電池においては、電荷Qを送り出す間、電圧は一定値Vです。従って、電池が供給する静電エネルギー、つまり、電池のする仕事は、
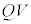と考えられます。コンデンサーが貯めこむ静電エネルギー
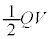とつじつまが合いません。
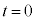から充分時間が経過するまでに抵抗Rで消費されるジュール熱Hを求めてみます。
つまり、電池が供給する静電エネルギーのうち半分は、抵抗でジュール熱として消費されてしまうので、コンデンサーには半分の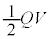
しか蓄えることができないのです。
超伝導のように抵抗がゼロでない限り、コンデンサーには、電池のした仕事の半分しか静電エネルギーを蓄えることはできません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
