電位(静電ポテンシャル)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
電位(静電ポテンシャル)をϕとして、電界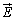
は、
空間に電界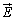
ができているとき、
と表せるような関数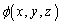
が存在します。この関数ϕを電位(静電ポテンシャル)と言います。
真空中で原点Oに電荷qが置かれているとき、空間内には、
という電界が発生しますが、これはrのみの関数です。
原点から半直線を引いてr軸とし、r軸上で、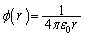
という関数を考えると、
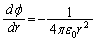(ϕがrのみの関数なので、
)
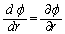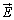のr方向成分
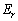について、
となります。
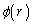と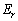
を比較すると、電位は電界の大きさに長さの次元を1つかけたものになっています。電界の単位は[N/C]なので、電位の単位は
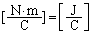です。
電位の単位を[V](ボルト)とすると、電界の単位は[V/m]となります。
単位でわかるように、電位に電荷をかけたものはエネルギーの次元を持ち、電位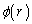
[V]の位置に電荷Q[C]が存在するとき、この電荷は位置エネルギー
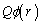[J]を持ちます。
この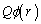
[J]を静電エネルギーと言います。
無限遠を位置エネルギーの基準にとり、原点Oに電荷qが置かれていて、電荷Qを無限遠から、原点Oよりrの位置まで持ってくるときの仕事Wを考えると、電荷Qはr方向に電気力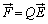
を受ける(rの位置まで持ってくる力は
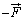です)ので、
となっています。
また、x方向に大きさEの一様な電界ができているとき、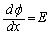
(一定)より、
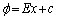(c：定数)と表せて、x方向に距離dの2点間には、電位差
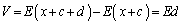が発生します。つまり、大きさEの一様な電界中の電界の向きに沿って距離dの2点間の電位差Vは、
です。電位差を電圧とも言います。
電界が球対称でない場合、あるいは、電界が一様でない場合には、電位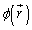
を求めるためには、線積分することが必要になります。即ち、電位の基準点からの経路
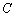に沿って、電界を積分し、
平面上で電位の等しい点を結んでできる曲線を等電位線、空間内で電位の等しい点を結んでできる曲面を等電位面と言います。
ある曲面、ある曲線に沿って、ϕが定数であれば、その方向では、
より、電界は成分を持たないので、電界ベクトル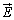
は、等電位線、等電位面に垂直になります。
平面上においては、等電位線は電気力線の直交截線(微分方程式の例3．を参照)になっています。
例えば、xy平面上の原点に正電荷が置かれている場合、電気力線を与える方程式は、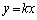
(k：定数)となりますが、
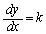と合わせて定数kを消去すると、
∴ 
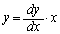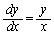
積分すると、
∴ 
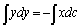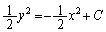(C：積分定数)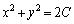
等電位線は円になります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
