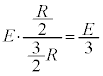京大物理'22年前期[2]
次の文章を読んで、 に適した式または数値を、それぞれの解答欄に記入せよ。なお、
に適した式または数値を、それぞれの解答欄に記入せよ。なお、 はすでに
はすでに で与えられたものと同じものを表す。また、問1では、指示にしたがって、解答を解答欄に記入せよ。
で与えられたものと同じものを表す。また、問1では、指示にしたがって、解答を解答欄に記入せよ。
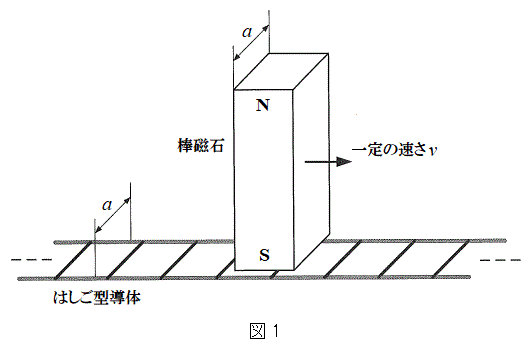 図1のように、水平面に無限の長さのはしご型導体が固定されており、その上に接触しないように少し隙間を設けて、直方体状の長い棒磁石が、図に示したN,Sの向きで鉛直に配置されている。なお、棒磁石の奥行方向の幅は、はしご型導体の幅と等しくaである。
図1のように、水平面に無限の長さのはしご型導体が固定されており、その上に接触しないように少し隙間を設けて、直方体状の長い棒磁石が、図に示したN,Sの向きで鉛直に配置されている。なお、棒磁石の奥行方向の幅は、はしご型導体の幅と等しくaである。
棒磁石を鉛直に保ったまま、図の右方向に水平に一定の速さvで動かしているときに、はしご型導体の各部分に生じる電流について考察する。なお、以下の議論では、はしご型導体のどの部分についても、その自己インダクタンスは無視できるものとし、棒磁石の磁化は変化しないものとする。
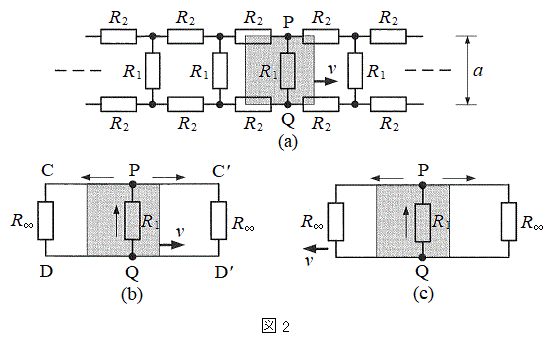 まず、棒磁石の端面の形状が、はしご型導体の格子のちょうど1区画に一致する場合を考える。はしご型導体は、図2(a)のように、抵抗のみからなる左右に無限に続く回路網であると考えることができる。いま、棒磁石が一定の速さvでPQを横切っているときを考える。なお、図の灰色の領域に生じている磁束密度Bは、紙面に垂直で、均一かつ一定であるとし、それ以外の領域の磁束密度は0とみなせるものとする。また、回路の各部分の抵抗値は、図中に示した
まず、棒磁石の端面の形状が、はしご型導体の格子のちょうど1区画に一致する場合を考える。はしご型導体は、図2(a)のように、抵抗のみからなる左右に無限に続く回路網であると考えることができる。いま、棒磁石が一定の速さvでPQを横切っているときを考える。なお、図の灰色の領域に生じている磁束密度Bは、紙面に垂直で、均一かつ一定であるとし、それ以外の領域の磁束密度は0とみなせるものとする。また、回路の各部分の抵抗値は、図中に示した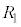 ,
,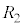 で与えられるものとする。電流については、各図に示した矢印の向きを正とする。
で与えられるものとする。電流については、各図に示した矢印の向きを正とする。
(1) ここでは、無限に続く回路網を、図2(b)の回路に置き換えて考える。すなわち、図2(a)のPQの左右両端の半無限部分が、それぞれ1つの抵抗値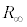 の抵抗に置き換えられているとする。図2(b)において、棒磁石がPQを横切っているとき、左の閉回路QPCDと、右の閉回路
の抵抗に置き換えられているとする。図2(b)において、棒磁石がPQを横切っているとき、左の閉回路QPCDと、右の閉回路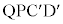 には、ともに同じ、大きさ
には、ともに同じ、大きさ の誘導起電力が発生する。したがって、QからPに流れる電流は
の誘導起電力が発生する。したがって、QからPに流れる電流は と求まる。電流が流れて抵抗において熱としてエネルギーが失われるから、棒磁石を一定の速さvで動かすには、単位時間当たり
と求まる。電流が流れて抵抗において熱としてエネルギーが失われるから、棒磁石を一定の速さvで動かすには、単位時間当たり の仕事をしなくてはならない。なお、回路を流れる電流を求めるとき、図2(c)のように、棒磁石が固定され、はしご型導体が速さvで左に動いていると考えても、結果は同じである。
の仕事をしなくてはならない。なお、回路を流れる電流を求めるとき、図2(c)のように、棒磁石が固定され、はしご型導体が速さvで左に動いていると考えても、結果は同じである。
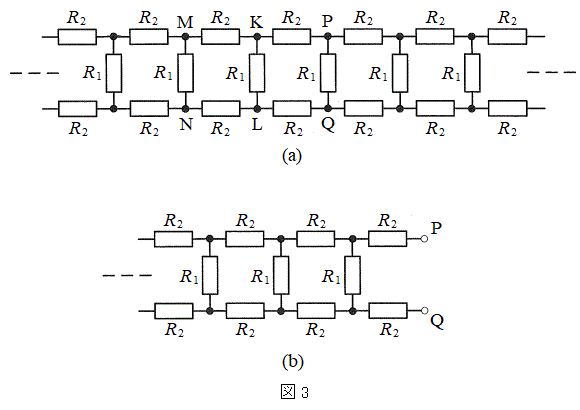 (2) 次に、はしご型導体と等価とみなした図3(a)に示す無限の回路網について考える。ここで、図3(a)は図2(a)と同じ無限の回路網である。図3(b)は、図3(a)の回路網をPとQで切り離した左側の部分である。一方で、この半無限回路網は、図3(a)の回路網を、KとL,あるいはMとNで切り離したものと考えることもできる。このことを利用すると、図3(b)に示す半無限回路網の合成抵抗値を求めることができる。また、その合成抵抗値によって、図3(a)の回路網のどの半無限部分でも、1つの抵抗に置き換えて考えることができる。
(2) 次に、はしご型導体と等価とみなした図3(a)に示す無限の回路網について考える。ここで、図3(a)は図2(a)と同じ無限の回路網である。図3(b)は、図3(a)の回路網をPとQで切り離した左側の部分である。一方で、この半無限回路網は、図3(a)の回路網を、KとL,あるいはMとNで切り離したものと考えることもできる。このことを利用すると、図3(b)に示す半無限回路網の合成抵抗値を求めることができる。また、その合成抵抗値によって、図3(a)の回路網のどの半無限部分でも、1つの抵抗に置き換えて考えることができる。
問1 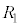 :
: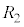 = 4:1のときには、図3(b)の半無限回路網の合成抵抗値
= 4:1のときには、図3(b)の半無限回路網の合成抵抗値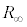 (端点Pと端点Qの間の抵抗値)が
(端点Pと端点Qの間の抵抗値)が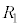 と同じになることを示せ。なお、説明のために、図を用いてよい。
と同じになることを示せ。なお、説明のために、図を用いてよい。
以下、図4,図5,図6の回路網は、図2(a)と同じ無限の回路網である。ただし、(3),(4),(5)においては、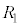 :
: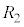 = 4:1の場合に限って考えることとし、
= 4:1の場合に限って考えることとし、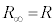 ,
,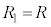 ,
,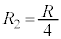 とおき、
とおき、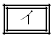 の起電力をEとおく。
の起電力をEとおく。
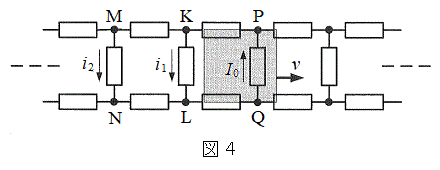 (3) 図4に示すQからPに流れる電流
(3) 図4に示すQからPに流れる電流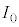 を、改めてRとEを用いて表すと
を、改めてRとEを用いて表すと である。また、(2)で述べたことを利用すれば、無限の回路網のあらゆる部分の電流を求めることができる。たとえば、KからLに流れる電流
である。また、(2)で述べたことを利用すれば、無限の回路網のあらゆる部分の電流を求めることができる。たとえば、KからLに流れる電流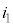 は、電流
は、電流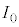 の
の 倍、MからNに流れる電流
倍、MからNに流れる電流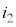 は、電流
は、電流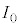 の
の 倍である。
倍である。
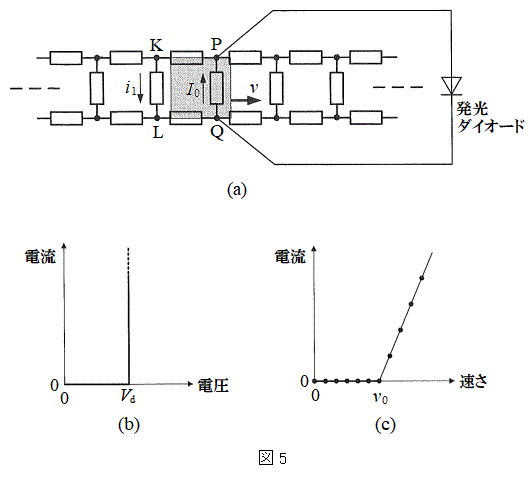 (4) 図5(a)のように、点Pと点Qに発光ダイオードを図に示した向きで接続する。この発光ダイオードの電流電圧特性は、図5(b)に示すように、順方向電圧が
(4) 図5(a)のように、点Pと点Qに発光ダイオードを図に示した向きで接続する。この発光ダイオードの電流電圧特性は、図5(b)に示すように、順方向電圧が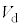 より小さいときは抵抗値が無限大、
より小さいときは抵抗値が無限大、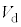 以上では抵抗値が0とみなせるものとする。なお、発光ダイオードを接続する導線は、抵抗やインダクタンスが無視でき、棒磁石のつくる磁束を横切らないものとする。
以上では抵抗値が0とみなせるものとする。なお、発光ダイオードを接続する導線は、抵抗やインダクタンスが無視でき、棒磁石のつくる磁束を横切らないものとする。棒磁石を動かす速さvと発光ダイオードに流れる電流の関係を測定したところ、図5(c)のような関係が得られた。図5(c)に示したように、発光ダイオードに電流が流れるのは、速さが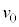 より大きいときであったが、その速さ
より大きいときであったが、その速さ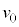 は
は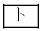 である。また、速さが
である。また、速さが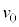 より大きいとき、回路網の各部分の電流をR,E,
より大きいとき、回路網の各部分の電流をR,E,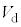 のうち必要なものを用いて表すと、QからPに流れる電流
のうち必要なものを用いて表すと、QからPに流れる電流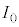 は
は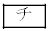 ,KからLに流れる電流
,KからLに流れる電流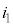 は
は ,発光ダイオードを流れる電流は
,発光ダイオードを流れる電流は である。
である。
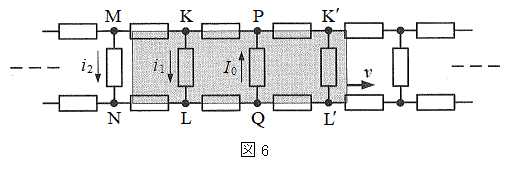 (5) つぎに、棒磁石の端面の形状が、はしご型導体の格子のちょうど3区画に一致する場合を考える(ただし、発光ダイオードは接続していない)。図6は、一定の速さvで移動している棒磁石による均一な磁束密度Bの範囲が、長方形
(5) つぎに、棒磁石の端面の形状が、はしご型導体の格子のちょうど3区画に一致する場合を考える(ただし、発光ダイオードは接続していない)。図6は、一定の速さvで移動している棒磁石による均一な磁束密度Bの範囲が、長方形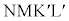 に一致していた位置から少し右に動いたときを表している。この場合、各部分を流れる電流は、(3)の結果を3つ重ね合わせることで容易に求めることができる。各部分の電流をR,Eを用いて表すと、QからPに流れる電流
に一致していた位置から少し右に動いたときを表している。この場合、各部分を流れる電流は、(3)の結果を3つ重ね合わせることで容易に求めることができる。各部分の電流をR,Eを用いて表すと、QからPに流れる電流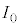 は
は ,KからLに流れる電流
,KからLに流れる電流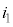 は
は ,MからNに流れる電流
,MからNに流れる電流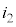 は
は である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 はしご型回路網とコの字型回路の融合問題ですが、問題文中にヒントがあるとはいえ、ダイオードが絡み、ボリュームもあって難題です。(5)の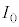 ,
,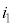 ,
,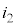 の値は(3)の
の値は(3)の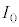 ,
,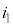 ,
,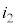 の値と異なるので、混乱しないように注意しましょう。
の値と異なるので、混乱しないように注意しましょう。
(1) 「棒磁石が固定され、はしご型導体が速さvで左に動いていると考えても、結果は同じである」というヒントから、フレミング右手の法則によりコの字型回路として考えます。上向き(人差し指の向き)の磁場中を導体棒が左向き(親指の向き)に動くと考えると起電力の向き(中指の向き)はQ→Pの向きで、起電力の大きさは、コの字型回路の公式より、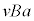 ......[イ]
......[イ]
起電力につながる抵抗は、図2(b)のCD間、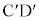 間の抵抗
間の抵抗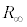 の並列接続の合成抵抗は
の並列接続の合成抵抗は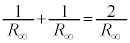 より
より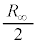 ,これと
,これと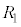 との直列接続の合成抵抗が
との直列接続の合成抵抗が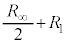 ,よって、QからPに流れる電流は、オームの法則により、
,よって、QからPに流れる電流は、オームの法則により、 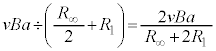 ......[ロ]
......[ロ]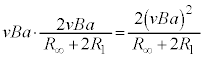 ......[ハ]
......[ハ]
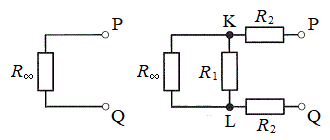 (2) 図2(b)のように、PQの左半分の半無限部分を1つの抵抗
(2) 図2(b)のように、PQの左半分の半無限部分を1つの抵抗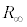 で置き換えて考えるのと同様に、図3(a)のKLから左側の半無限部分を
で置き換えて考えるのと同様に、図3(a)のKLから左側の半無限部分を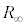 で置き換えて考えると、右図の右側の図でPQ間に接続されている抵抗は
で置き換えて考えると、右図の右側の図でPQ間に接続されている抵抗は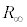 に等しくなります。KL間の
に等しくなります。KL間の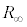 と
と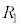 の並列接続の合成抵抗は、
の並列接続の合成抵抗は、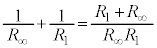 より、
より、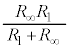 ,これと2個の
,これと2個の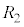 との直列接続の合成抵抗は、
との直列接続の合成抵抗は、これが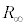 に等しく、
に等しく、 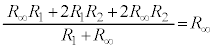 ∴
∴ 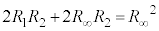 ・・・①
・・・①
問1 ①で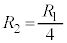 として、
として、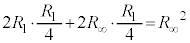
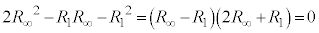 ∴
∴ 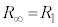 注.説明のために図を付ける場合は、右上図で
注.説明のために図を付ける場合は、右上図で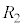 を
を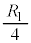 とした図を付けます。
とした図を付けます。
以後、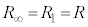 ,
,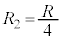 とします。
とします。
(3) [ロ]で見たように、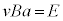 であって、合成抵抗は2個の
であって、合成抵抗は2個の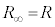 の並列と
の並列と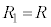 の直列として
の直列として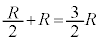 より、電流は、
より、電流は、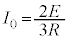 ......[ニ]
......[ニ] 図4において、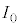 はPで左右に分かれて
はPで左右に分かれて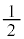 になり、Kで
になり、Kで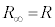 (KLの左側の無限回路網を
(KLの左側の無限回路網を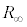 )と
)と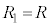 に分かれて
に分かれて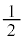 ずつになり、
ずつになり、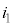 は
は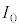 の
の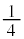 倍になります。
倍になります。 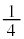 ......[ホ]さらに、KからMに行くと、Kと同様に
......[ホ]さらに、KからMに行くと、Kと同様に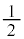 ずつ分かれて、
ずつ分かれて、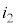 は
は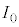 の
の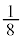 倍になります。
倍になります。 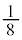 ......[ヘ]
......[ヘ]
(4) (3)[ニ]で見たように、PQ間の電圧即ち抵抗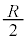 (2個の
(2個の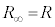 の並列)両端の電圧は、
の並列)両端の電圧は、 速さが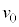 のとき
のとき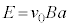 ,そのときのPQ間の電圧が
,そのときのPQ間の電圧が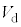 のときに発光ダイオードに電流が流れるので、
のときに発光ダイオードに電流が流れるので、 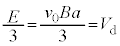 ∴
∴ 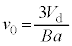 ......[ト]
......[ト]速さが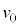 より大きいとき、発光ダイオードに電流が流れ、図5(b)より発光ダイオードの電圧は
より大きいとき、発光ダイオードに電流が流れ、図5(b)より発光ダイオードの電圧は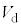 で一定になります。PQ間の抵抗Rにかかる電圧は
で一定になります。PQ間の抵抗Rにかかる電圧は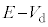 ,QからPに流れる電流は、
,QからPに流れる電流は、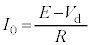 ......[チ]
......[チ]
PQ間の電圧は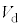 で一定で、図2(c)を参考にすると、PQ間には発光ダイオード以外に等価的に抵抗
で一定で、図2(c)を参考にすると、PQ間には発光ダイオード以外に等価的に抵抗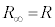 が2個並列に接続されておりそれぞれに電流
が2個並列に接続されておりそれぞれに電流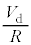 が流れます。ここで(2)の図の右側の図を見ると、抵抗
が流れます。ここで(2)の図の右側の図を見ると、抵抗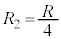 に電流
に電流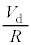 が流れ、電圧降下
が流れ、電圧降下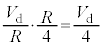 を生じます。抵抗
を生じます。抵抗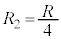 はP側Q側それぞれに1個ずつあるので、ここでの電圧降下は
はP側Q側それぞれに1個ずつあるので、ここでの電圧降下は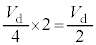 ,KL間の電圧は
,KL間の電圧は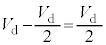 です。オームの法則よりKL間の抵抗Rに流れる電流は、
です。オームの法則よりKL間の抵抗Rに流れる電流は、 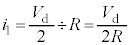 ......[リ]
......[リ]図5(a)において、QからPに流れる電流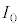 のうち、K側に
のうち、K側に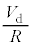 ,Kと反対側に
,Kと反対側に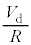 が流れるので、発光ダイオードに流れる電流は、残りの
が流れるので、発光ダイオードに流れる電流は、残りの 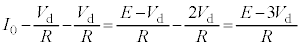 ......[ヌ]
......[ヌ]
(5) 問題文のヒント通りに(3)の結果を3つ重ね合わせて考えます。図6において、PQ間に生じる起電力による電流は、(3)の結果より、PQ間に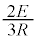 ,KL間に
,KL間に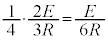 ,MN間に
,MN間に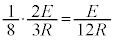 ,KL間に生じる起電力による電流は、KL間に(LからKに向かう向き)
,KL間に生じる起電力による電流は、KL間に(LからKに向かう向き)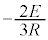 ,MN間に
,MN間に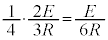 ,PQ間に(PからQに向かう向き)
,PQ間に(PからQに向かう向き)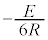 ,
,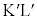 間に生じる起電力による電流は、PQ間に(PからQに向かう向き)
間に生じる起電力による電流は、PQ間に(PからQに向かう向き)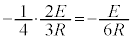 ,KL間に
,KL間に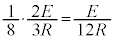 ,MN間に(3)と同様に考えて
,MN間に(3)と同様に考えて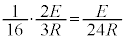
PからQに流れる電流は、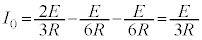 ......[ル]
......[ル]
KからLに流れる電流は、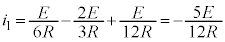 ......[ヲ]
......[ヲ]
MからNに流れる電流は、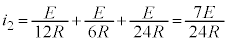 ......[ワ]
......[ワ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 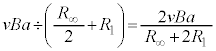 ......[ロ]
......[ロ]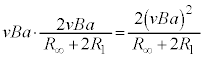 ......[ハ]
......[ハ]