���s��w2025�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�܂��A��1�ł́A�w���ɂ��������āA�����ɋL������B�������A�~������π�C�d�͉����x��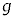 �Ƃ���B
�Ƃ���B
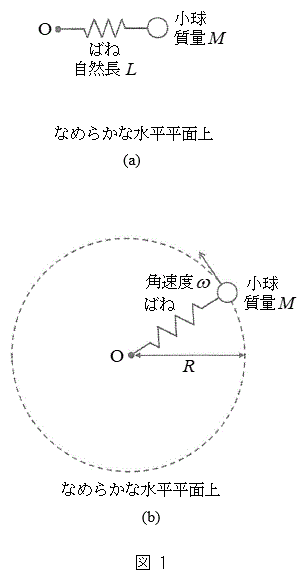 (1) �}1(a)�̂悤�Ȏ��R��L�Ŏ��ʂ������ł���˂̈�[�ɁA����M�ő傫���������ł��鏬�������t�����B���̂˂̂˒萔��k�ł���B��̂ƂȂ����˂Ə������A�Ȃ߂炩�Ȑ������ʏ�ɒu���A�������t���Ă��Ȃ����̂˂̒[���A�������ʏ�̓_O�ɌŒ肵���B�˂͓_O�̂܂������R�ɉ�]�ł���B
(1) �}1(a)�̂悤�Ȏ��R��L�Ŏ��ʂ������ł���˂̈�[�ɁA����M�ő傫���������ł��鏬�������t�����B���̂˂̂˒萔��k�ł���B��̂ƂȂ����˂Ə������A�Ȃ߂炩�Ȑ������ʏ�ɒu���A�������t���Ă��Ȃ����̂˂̒[���A�������ʏ�̓_O�ɌŒ肵���B�˂͓_O�̂܂������R�ɉ�]�ł���B�������ʏ�ŁA������_O�̂܂��ŁA������̊p���xω(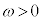 )�œ����~�^���������Ƃ��A�˂͐L�тāA�}1(b)�̂悤�ɓ_O���珬���܂ł̋�����R�ł������B�˂̕����͂ɂ�菬���ɂ͓_O�̕����֑傫���@�A�@�̗͂��������Ă���B�܂������ɂ͓_O���牓����������֑傫���@�C�@�̉��S�͂��������Ă���B���̕����֓��������̗͂̑傫���́A��������_O���珬���܂ł̋����Ɉˑ�����B���Ȃ킿�A�p���x��ω�̏ꍇ�ɁA���҂̑傫�����������Ȃ�_O���珬���܂ł̋�����R�ł���A�����k�CM�CL�Cω��p�����@�E�@�ƕ\�����B
)�œ����~�^���������Ƃ��A�˂͐L�тāA�}1(b)�̂悤�ɓ_O���珬���܂ł̋�����R�ł������B�˂̕����͂ɂ�菬���ɂ͓_O�̕����֑傫���@�A�@�̗͂��������Ă���B�܂������ɂ͓_O���牓����������֑傫���@�C�@�̉��S�͂��������Ă���B���̕����֓��������̗͂̑傫���́A��������_O���珬���܂ł̋����Ɉˑ�����B���Ȃ킿�A�p���x��ω�̏ꍇ�ɁA���҂̑傫�����������Ȃ�_O���珬���܂ł̋�����R�ł���A�����k�CM�CL�Cω��p�����@�E�@�ƕ\�����B
��1�@�}1(b)�̏������s�������~�^�����s�����߂̏����o���A�p���xω(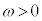 )�͈̔͂Ŏ����B
)�͈̔͂Ŏ����B
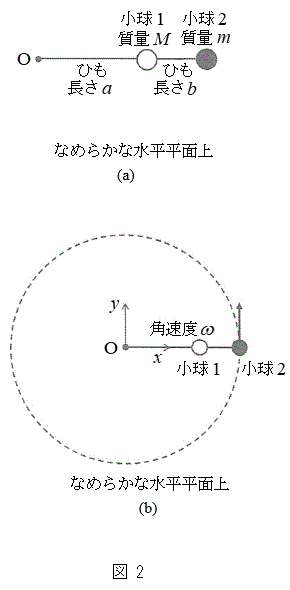 (2) �}2(a)�̂悤�ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����a�̂Ђ��̈�[���A�Ȃ߂炩�Ȑ������ʏ�̓_O�ɌŒ肵���B�܂��A���̂Ђ��̂�������̒[�ɁA����M�ő傫���������ł��鏬��1�����t�����B����1�ɂ͂���ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����b�̂Ђ��̈�[�����t���A���̂Ђ��̑��[�ɂ͎���m�ő傫���������ł��鏬��2�����t�����B
(2) �}2(a)�̂悤�ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����a�̂Ђ��̈�[���A�Ȃ߂炩�Ȑ������ʏ�̓_O�ɌŒ肵���B�܂��A���̂Ђ��̂�������̒[�ɁA����M�ő傫���������ł��鏬��1�����t�����B����1�ɂ͂���ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����b�̂Ђ��̈�[�����t���A���̂Ђ��̑��[�ɂ͎���m�ő傫���������ł��鏬��2�����t�����B�͂��߁A2�̏�����2�{�̂Ђ��́A�꒼����ɘA�����ꂽ�܂܁A�Ȃ߂炩�Ȑ������ʏ�ŁA�_O�𒆐S�Ƃ���p���xω�̓����~�^�������Ă����B�}2(b)���Ɏ����ʂ�A�_O�����W���_�Ƃ��A�������ʏ�̂��������x�����A����Ɛ����ȕ�����y�����Ƃ�B��]���Ă��鏬��2�̍��W��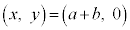 �̂Ƃ�(�}2(b))�A����a�̂Ђ����ꂽ�B�ꂽ�u�Ԃ̎�����
�̂Ƃ�(�}2(b))�A����a�̂Ђ����ꂽ�B�ꂽ�u�Ԃ̎�����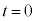 �Ƃ���B�Ȃ��ꂽ��̂Ђ��́A���̌��2�̏����̉^���ɂ͉e����^���Ȃ����̂Ƃ���B
�Ƃ���B�Ȃ��ꂽ��̂Ђ��́A���̌��2�̏����̉^���ɂ͉e����^���Ȃ����̂Ƃ���B
����b�̂Ђ��ŘA�����ꂽ2�̏����̉^���ɒ��ڂ���B�Ђ����ꂽ�����2�̏����̏d�S�̈ʒu��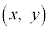 = (�@�G�@�C�@�I�@)�ł���B���̂Ƃ��d�S���猩������1�̑��Α��x�̑傫�����@�J�@�ł���A���̌�����{�L�F�@x�����̕����C�Ax�����̕����C�By�����̕����C�Cy�����̕���}�ł���B�d�S���猩������2�̑��Α��x�̑傫����������A����1�̂����Ɠ��l�ɋ��߂邱�Ƃ��ł���B����1�Ə���2��A�����钷��b�̂Ђ��ɂ������Ă��钣�͂��@�N�@�ł���A2�̏����͏d�S�܂����p���x�@�P�@�ʼn�]����B�܂��A�d�S�̉^����2�̏����̎��ʂ��d�S�ɏW���������̂Ƃ��čl���邱�Ƃ��ł���B�d�S�ɂ���������x�̑傫�����@�R�@�ł��邱�Ƃ���A�d�S��{�T�F�@�~�^���C�A�����^���C�B�P�U��}���邱�Ƃ��킩��B
= (�@�G�@�C�@�I�@)�ł���B���̂Ƃ��d�S���猩������1�̑��Α��x�̑傫�����@�J�@�ł���A���̌�����{�L�F�@x�����̕����C�Ax�����̕����C�By�����̕����C�Cy�����̕���}�ł���B�d�S���猩������2�̑��Α��x�̑傫����������A����1�̂����Ɠ��l�ɋ��߂邱�Ƃ��ł���B����1�Ə���2��A�����钷��b�̂Ђ��ɂ������Ă��钣�͂��@�N�@�ł���A2�̏����͏d�S�܂����p���x�@�P�@�ʼn�]����B�܂��A�d�S�̉^����2�̏����̎��ʂ��d�S�ɏW���������̂Ƃ��čl���邱�Ƃ��ł���B�d�S�ɂ���������x�̑傫�����@�R�@�ł��邱�Ƃ���A�d�S��{�T�F�@�~�^���C�A�����^���C�B�P�U��}���邱�Ƃ��킩��B
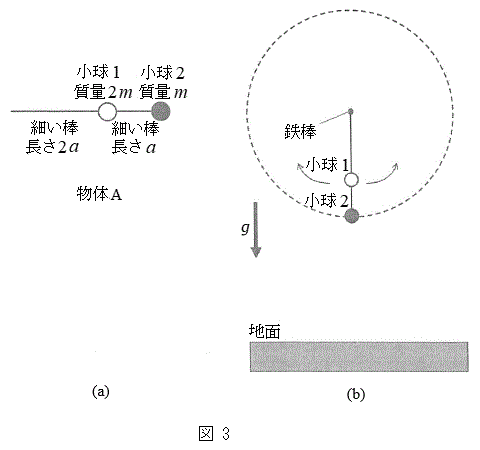 (3) �}3(a)�̂悤�ȁA���ʂ������ł���2�{�̕ό`���Ȃ��ׂ��_�ƁA�傫���������ł���2�̏������A�����ꂽ����A���쐻�����B�܂�����
(3) �}3(a)�̂悤�ȁA���ʂ������ł���2�{�̕ό`���Ȃ��ׂ��_�ƁA�傫���������ł���2�̏������A�����ꂽ����A���쐻�����B�܂�����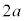 �ׂ̍��_�̈�[�Ɏ���
�ׂ̍��_�̈�[�Ɏ���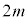 �̏���1��ڒ������B����1�ɂ͂���ɁA����a�ׂ̍��_�̈�[���Œ肵�A����ɂ��ׂ̍��_�̑��[�ɂ͎���m�̏���2���Œ肵���B����
�̏���1��ڒ������B����1�ɂ͂���ɁA����a�ׂ̍��_�̈�[���Œ肵�A����ɂ��ׂ̍��_�̑��[�ɂ͎���m�̏���2���Œ肵���B����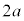 �ׂ̍��_�ƒ���a�ׂ̍��_�́A���ꂼ��̎��̉����������S�Ɉ�v���Ă���B
�ׂ̍��_�ƒ���a�ׂ̍��_�́A���ꂼ��̎��̉����������S�Ɉ�v���Ă���B�����Ȓn�ʂ��炠�鍂���̈ʒu�ɁA�n�ʂɕ��s�ɐݒu���ꂽ�܂������ōׂ��S�_������B�����ɍ쐻��������A���\������ׂ��_�́A������̏����Ƃ��ڑ�����Ă��Ȃ���[���A���̓S�_�ɐ����Ɏ��t�����B�}3(b)�́A����A�����t�����_���܂ޓS�_�ɐ����ȕ��ʂ��A�S�_�̎��������猩���}�ł���B�A�����ꂽ����A�́A�S�_�ɐ����Ȃ��̕��ʓ��ŁA�S�_�̂܂������R�ɉ�]�ł���B
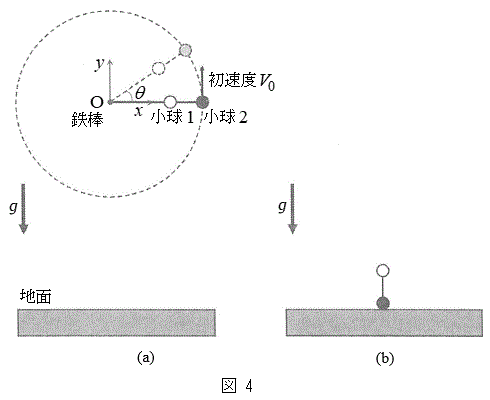 �͂��߁A����A���}4(a)�̂悤�ɒn�ʂƕ��s�ƂȂ�悤�ɕێ�����Ă���B���W���_O��S�_�̈ʒu�ɂƂ�A�������珬��2�̕�����x�����̕����A���������y�����̕����Ƃ���B�܂��}4(a)���Ɏ����ʂ�Ax������̉�]�p��θ(�����v���𐳁A�P�ʂ����W�A��)�ŕ\���B������
�͂��߁A����A���}4(a)�̂悤�ɒn�ʂƕ��s�ƂȂ�悤�ɕێ�����Ă���B���W���_O��S�_�̈ʒu�ɂƂ�A�������珬��2�̕�����x�����̕����A���������y�����̕����Ƃ���B�܂��}4(a)���Ɏ����ʂ�Ax������̉�]�p��θ(�����v���𐳁A�P�ʂ����W�A��)�ŕ\���B������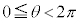 �Ƃ��A���Ƃ���y�����̕�����
�Ƃ��A���Ƃ���y�����̕�����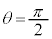 �ŕ\�����B
�ŕ\�����B
����A��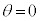 �̈ʒu�ɂ���Ƃ��A������������������x������2�ɗ^�����B����2�̏����x��
�̈ʒu�ɂ���Ƃ��A������������������x������2�ɗ^�����B����2�̏����x��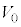 �Ƃ���ƁA���̂Ƃ�����A�̂��^���G�l���M�[���@�V�@�Ə�����B�܂��A
�Ƃ���ƁA���̂Ƃ�����A�̂��^���G�l���M�[���@�V�@�Ə�����B�܂��A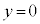 ���ʒu�G�l���M�[�̊�����Ƃ���ƁA�����x��^����ꂽ�̂��A����A����]���ĉ�]�p��θ�ƂȂ����Ƃ��ɁA����A�����ʒu�G�l���M�[���@�X�@�Ə�����B
���ʒu�G�l���M�[�̊�����Ƃ���ƁA�����x��^����ꂽ�̂��A����A����]���ĉ�]�p��θ�ƂȂ����Ƃ��ɁA����A�����ʒu�G�l���M�[���@�X�@�Ə�����B
�ȉ��ł�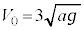 �Ƃ��āA
�Ƃ��āA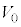 ��p�����ɉ���B
��p�����ɉ���B
����A�����߂�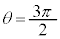 �̈ʒu�ɓ��B���钼�O�ɂ́A����A�͐}4(a)�̕������猩���Ƃ�{�Z�F�@���v���C�A�����v���}�ɉ�]���Ă���B
�̈ʒu�ɓ��B���钼�O�ɂ́A����A�͐}4(a)�̕������猩���Ƃ�{�Z�F�@���v���C�A�����v���}�ɉ�]���Ă���B
����A��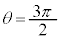 �̈ʒu�ɓ��B�����Ƃ��A���̉�]�̊p���x�̑傫�����@�\�@�ł���B���̂Ƃ��A�ڒ����Ă���������
�̈ʒu�ɓ��B�����Ƃ��A���̉�]�̊p���x�̑傫�����@�\�@�ł���B���̂Ƃ��A�ڒ����Ă���������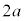 �ׂ̍��_�Ə���1�̘A��������u�ŊO�ꂽ�B�A�����O�ꂽ�u�Ԃ̎�����
�ׂ̍��_�Ə���1�̘A��������u�ŊO�ꂽ�B�A�����O�ꂽ�u�Ԃ̎�����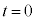 �Ƃ���B����a�ׂ̍��_�ŘA�����ꂽ2�̏����́A
�Ƃ���B����a�ׂ̍��_�ŘA�����ꂽ2�̏����́A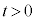 �ł̉^�����l����B
�ł̉^�����l����B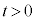 �ŏ��߂ď���2������1�̉��������ɓ��B�����Ƃ��A���傤�Ǐ���2���n�ʂɐڂ���(�}4(b))�B����āA�n�ʂ���Ƃ��āA�S�_�̍������@�^�@�ł���Ƌ��߂���B
�ŏ��߂ď���2������1�̉��������ɓ��B�����Ƃ��A���傤�Ǐ���2���n�ʂɐڂ���(�}4(b))�B����āA�n�ʂ���Ƃ��āA�S�_�̍������@�^�@�ł���Ƌ��߂���B
[��]
[2]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�`��3�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A�~������π�Ƃ��A�ȉ��ɓo�ꂷ�镨����C�̂̓������͂��ׂ�μ�Ƃ���B
 (1) �}1�̂悤�ɁA����d�C���ar�̉~���ɒ�R�̖����ł��铱������l��N���t���č�����\���m�C�h(�ȉ��R�C���ƌĂ�)������B�~�������͋C�̂Ŗ�������Ă���A�R�C���̒���d��r�Ɣ�ׂď\�������A���̃R�C���ɓd���𗬂��Ɖ~�������ɂ͈�l�Ȏ������x���ł���B���̃R�C���ɊO���d����ڑ����ēd��I�𗬂����Ƃ��ɉ~�������ɔ������鎥�����x�̑傫�����@�C�@�ł���B
(1) �}1�̂悤�ɁA����d�C���ar�̉~���ɒ�R�̖����ł��铱������l��N���t���č�����\���m�C�h(�ȉ��R�C���ƌĂ�)������B�~�������͋C�̂Ŗ�������Ă���A�R�C���̒���d��r�Ɣ�ׂď\�������A���̃R�C���ɓd���𗬂��Ɖ~�������ɂ͈�l�Ȏ������x���ł���B���̃R�C���ɊO���d����ڑ����ēd��I�𗬂����Ƃ��ɉ~�������ɔ������鎥�����x�̑傫�����@�C�@�ł���B���ɁA��������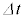 �̊Ԃɓd����I����
�̊Ԃɓd����I����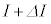 �ɂ������ω�������ƁA�R�C���ɂ͗U���N�d���@���@�~
�ɂ������ω�������ƁA�R�C���ɂ͗U���N�d���@���@�~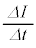 ����������(
����������(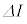 �͔����ʂł���A�N�d�͂̕����͓d���̏㗬���̓d�ʂ������ꍇ�𐳂Ƃ���)�B���̂��Ƃ���A���̃R�C���̎��ȃC���_�N�^���X���@�n�@�ł���B�܂��A����
�͔����ʂł���A�N�d�͂̕����͓d���̏㗬���̓d�ʂ������ꍇ�𐳂Ƃ���)�B���̂��Ƃ���A���̃R�C���̎��ȃC���_�N�^���X���@�n�@�ł���B�܂��A����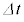 �̊ԂɊO���d�����R�C���ɂ����d�����@�j�@�~
�̊ԂɊO���d�����R�C���ɂ����d�����@�j�@�~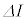 �ł���B
�ł���B
�}1�̃R�C���ɓd��I������Ă���Ƃ��A�R�C���ɂ̓G�l���M�[�@�z�@���~�����Ă���B�R�C���𗬂��d����I����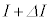 �ɕω�����ۂ̂��̃G�l���M�[�̑����́A
�ɕω�����ۂ̂��̃G�l���M�[�̑����́A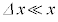 �����\��������
�����\��������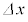 �ɑ��Đ�������ߎ���
�ɑ��Đ�������ߎ��� 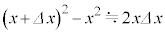 �@���(i)
�@���(i)���g�����@�j�@�~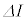 �ƂȂ�A�O���d�����R�C���ɂ����d���ƈ�v����B�܂�A�O���d�����s�����d�����R�C���̃G�l���M�[�Ƃ��Ē~�ς����B
�ƂȂ�A�O���d�����R�C���ɂ����d���ƈ�v����B�܂�A�O���d�����s�����d�����R�C���̃G�l���M�[�Ƃ��Ē~�ς����B
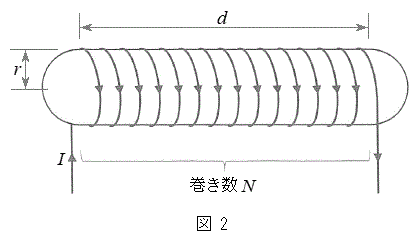 (2) �}2�̂悤�ɁA�o���[���A�[�g�p�̕��D�̂悤�ȍג����~���`��������L�k���݂̕������ɁA�L�k���݂Œ�R�̖����ł��铱�������������x(�~���������̒P�ʒ���������̓����̖{��)����l�ƂȂ�悤��N���t���č�����\���m�C�h(�ȉ��R�C���ƌĂ�)������B�������̋C�̗̂ʂ͒����ł��A���̂Ƃ����͉~���`���ۂ����܂ܔ��a�Ⓑ�����ς��B�����͖��ɐڒ�����Ă���A���̔��a�Ⓑ�����ω�����Ƃ������͖��ɐڂ����܂܂ނ�Ȃ��L�яk�݂��A���������x�͈�l�ɕۂ������̂Ƃ���B�܂��A���͌��݂̖����ł���≏�̂łł��Ă���A���Ɠ����͗e�ՂɐL�k������̂Ƃ��A���̖ʐρA�����̒�������ь`��̕ω��ɗv����d���͏\�������������ł�����̂Ƃ���B
(2) �}2�̂悤�ɁA�o���[���A�[�g�p�̕��D�̂悤�ȍג����~���`��������L�k���݂̕������ɁA�L�k���݂Œ�R�̖����ł��铱�������������x(�~���������̒P�ʒ���������̓����̖{��)����l�ƂȂ�悤��N���t���č�����\���m�C�h(�ȉ��R�C���ƌĂ�)������B�������̋C�̗̂ʂ͒����ł��A���̂Ƃ����͉~���`���ۂ����܂ܔ��a�Ⓑ�����ς��B�����͖��ɐڒ�����Ă���A���̔��a�Ⓑ�����ω�����Ƃ������͖��ɐڂ����܂܂ނ�Ȃ��L�яk�݂��A���������x�͈�l�ɕۂ������̂Ƃ���B�܂��A���͌��݂̖����ł���≏�̂łł��Ă���A���Ɠ����͗e�ՂɐL�k������̂Ƃ��A���̖ʐρA�����̒�������ь`��̕ω��ɗv����d���͏\�������������ł�����̂Ƃ���B�Ȃ��A�ȉ��ł͕K�v�ɉ����ċߎ���(i)���g����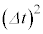 �����A���ɂ�
�����A���ɂ�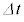 ���g�킸�ɉ��L������B
���g�킸�ɉ��L������B
�܂��A�R�C���̗��[���Œ葕�u�ŌŒ肵�ē����Ȃ��悤�ɂ��A���̒�����d�ɕۂ����悤�ɂ����B���̏�ԂŃR�C���ɓd��I�𗬂��A�������̋C�̗̂ʂ����āA�}2�̂悤�ɃR�C���̔��a��r�ƂȂ��Ԃ�������B���̂Ƃ��A�R�C�������ɂ͈�l�Ȏ������x�@�C�@�����������B���̏�Ԃ���A�d��I�����ɕۂ����܂ܖ������̋C�̗̂ʂ�������葝���������Ƃ���A�R�C���̔��a�͑���v�ő傫���Ȃ�A��������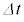 �̂̂���
�̂̂���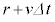 �ɂȂ����B���̂Ƃ��A�R�C���ꊪ�����т�������
�ɂȂ����B���̂Ƃ��A�R�C���ꊪ�����т�������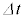 �̊Ԃ�
�̊Ԃ�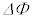 = �@�w�@�~
= �@�w�@�~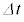 ������������̂ŁA�R�C���ɂ͗U���N�d���@�g�@����������(�N�d�͂̕����͓d���̏㗬���̓d�ʂ������Ƃ��𐳂Ƃ���)�B�܂��A����
������������̂ŁA�R�C���ɂ͗U���N�d���@�g�@����������(�N�d�͂̕����͓d���̏㗬���̓d�ʂ������Ƃ��𐳂Ƃ���)�B�܂��A����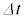 �̊ԂɊO���d�����R�C���ɑ��čs���d�����@�`�@�~
�̊ԂɊO���d�����R�C���ɑ��čs���d�����@�`�@�~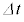 �ł���B
�ł���B
����A�R�C���ɒ~������G�l���M�[(�@�z�@)�́A�R�C�����a���傫���Ȃ������Ƃɂ�莞��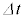 �̊Ԃ��@���@�~
�̊Ԃ��@���@�~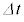 ������������B���̃G�l���M�[�̕ω��́A�O���d�����s�����d���@�`�@�ƁA�����O�̋C�̂̈��͍������ɑ��čs�����d���̘a�ɓ������B����
������������B���̃G�l���M�[�̕ω��́A�O���d�����s�����d���@�`�@�ƁA�����O�̋C�̂̈��͍������ɑ��čs�����d���̘a�ɓ������B����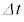 �̊ԂɃR�C���̑̐ς��@�k�@�~
�̊ԂɃR�C���̑̐ς��@�k�@�~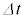 ������������̂ŁA�����O�̈��͍���
������������̂ŁA�����O�̈��͍��� 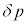 = (�O���̋C�̂̈���)�|(�����̋C�̂̈���)
= (�O���̋C�̂̈���)�|(�����̋C�̂̈���)�Ƃ���ƁA�����O�̋C�̂̈��͍�������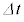 �̊Ԃɂɖ��ɑ��čs���d����
�̊Ԃɂɖ��ɑ��čs���d����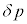 ���g�����@���@�~
���g�����@���@�~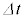 �Ə�����B�ȏ�̂��Ƃ��疌���O�̋C�̂̈��͍�
�Ə�����B�ȏ�̂��Ƃ��疌���O�̋C�̂̈��͍�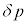 �����߂邱�Ƃ��ł��Aμ���@�C�@�ŋ��߂��R�C�������̎������xB�݂̂�p���ĕ\����
�����߂邱�Ƃ��ł��Aμ���@�C�@�ŋ��߂��R�C�������̎������xB�݂̂�p���ĕ\����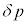 = �@���@�Ə�����B
= �@���@�Ə�����B
���܁A���ɂ͖����O�̋C�̂������炷���͍��ɉ����A�d��I�����o�����͂������Ă���B�����̈��͂��荇���̏����������Ƃ���A�d��I�����o�����͂́A{���F�@�R�C����c��܂�������ɓ����Ă���C�A�R�C�������k����������ɓ����Ă���C�B�����Ă��Ȃ�}�B
(3) �R�C����}2�̏�Ԃɖ߂��Ă���A�R�C���̔��a��r�ɌŒ肵�������ŃR�C���̉~���������̒��������R�ɕω���������悤�ɂ����B�R�C���̉~��������������d�̏�Ԃ���A�d��I�����ɕۂ����܂ܖ��̓����̋C�̗ʂ�ω��������Ƃ���A�~���������̒���������v�ł������Ƒ傫���Ȃ�A��������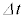 �̂̂���
�̂̂���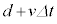 �ɂȂ����B���̂Ƃ��A
�ɂȂ����B���̂Ƃ��A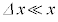 �����\��������
�����\��������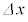 �ɑ��Đ��藧�ߎ���
�ɑ��Đ��藧�ߎ��� 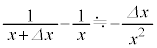 �@���(ii)
�@���(ii)���g����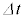 ��2���ȏ�̍�������ƁA��������
��2���ȏ�̍�������ƁA��������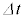 �̊ԂɊO���d�����R�C���ɑ��čs���d�����@�J�@�~
�̊ԂɊO���d�����R�C���ɑ��čs���d�����@�J�@�~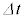 �ł��邱�Ƃ�������B���̂Ƃ���1�`��3�ɓ�����B
�ł��邱�Ƃ�������B���̂Ƃ���1�`��3�ɓ�����B
��1�@�����O�̋C�̂̈��͍���
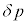 = (�O���̋C�̂̈���)�|(�����̋C�̂̈���)
= (�O���̋C�̂̈���)�|(�����̋C�̂̈���)�Ƃ���Ƃ��A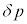 �����߂�B�������A�ߎ���(ii)���g����
�����߂�B�������A�ߎ���(ii)���g����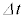 ��2���ȏ�̍������A�ɂ�μ���@�C�@�ŋ��߂��R�C�������̎������xB�݂̂�p����B
��2���ȏ�̍������A�ɂ�μ���@�C�@�ŋ��߂��R�C�������̎������xB�݂̂�p����B
��2�@�d��I���R�C���̗��[�ʂɍ��o�����͂̌����ɂ��āA�K�Ȃ��̂��ȉ�����I��Ŕԍ������ɋL������B
�@�@�R�C�����~���������ɐL�т悤�Ƃ��鈳�͂������Ă���B
�A�@�R�C�����~���������ɏk�����Ƃ��鈳�͂������Ă���B
�B�@���͓͂����Ă��Ȃ��B
��3�@��2�̌��ʂ��A�R�C�����`������e�ꊪ���̓����𗬂��d�������݂ɋy�ڂ��͂ɂ��ĊȌ��ɐ�������B
[��]
[3]�@���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B
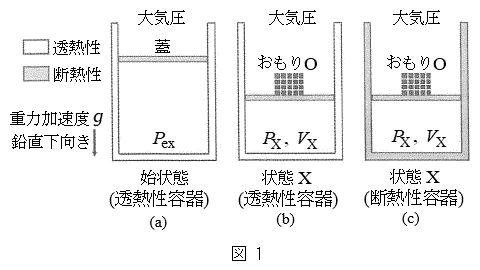 (1) 1�����̒P���q���q���z�C�̂̏�ԕω��ɂ��čl����B��Ή��xT�ɂ����邱�̋C�̂̓����G�l���M�[�́AR���C�̒萔�Ƃ����
(1) 1�����̒P���q���q���z�C�̂̏�ԕω��ɂ��čl����B��Ή��xT�ɂ����邱�̋C�̂̓����G�l���M�[�́AR���C�̒萔�Ƃ����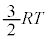 �ł���B�܂��A�������Ƃ����f�M�ω��ł́A���̋C�̂̈���P�Ƒ̐�V�̊Ԃɂ̓|�A�\���̎�
�ł���B�܂��A�������Ƃ����f�M�ω��ł́A���̋C�̂̈���P�Ƒ̐�V�̊Ԃɂ̓|�A�\���̎�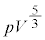 = ��肪���藧�B�ȉ��A�d�͉����x�̑傫����
= ��肪���藧�B�ȉ��A�d�͉����x�̑傫����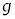 �Ƃ���B
�Ƃ���B
�}1(a)�Ɏ����悤�ɁA���̗��z�C�̂�f�ʐς�S�̉~����̗e��ɓ���A�W�ŕ�����B�W�͒f�M���ł���A�C���������킸�ɉ��������Ɋ��炩�ɓ������Ƃ��ł���B�e��͓��M���ƒf�M���ɐ�ւ��邱�Ƃ��ł��A�͂��ߓ��M���ł���B�܂��A�e��͏\���ɐ[���W���O��邱�Ƃ͂Ȃ��B�W�ɂ�����d�͂ɂ�鈳�͂Ƒ�C���Ƃ����킹�����͂�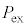 �Ƃ���B
�Ƃ���B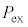 �Ɨ��z�C�̂̈��͂��ނ荇���A�W�͐Î~���Ă���B�e��͓��M���̂��ߊO���ƔM�̂���肪�\�������s���A���z�C�̂̉��x�͎��͂̑�C�Ɠ����ł���B���̏�Ԃ��n��ԂƌĂԁB
�Ɨ��z�C�̂̈��͂��ނ荇���A�W�͐Î~���Ă���B�e��͓��M���̂��ߊO���ƔM�̂���肪�\�������s���A���z�C�̂̉��x�͎��͂̑�C�Ɠ����ł���B���̏�Ԃ��n��ԂƌĂԁB
�n��Ԃɂ����ĊW�Ɏ���M�̂�����O��Â��ɍڂ��A�������ƋC�̂����k����ƁA�C�̂̈��͂Ƒ̐ς����ꂼ��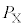 �C
�C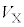 �ŊW�͐Î~�����B���̏�Ԃ����X�Ƃ���(�}1(b))�B
�ŊW�͐Î~�����B���̏�Ԃ����X�Ƃ���(�}1(b))�B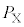 = �@���@�ł���B
= �@���@�ł���B
���ɁA���X�ɂ���e���f�M���ɐ�ւ��A�O�E�Ƃ̔M�̏o���肪�ł��Ȃ��悤�ɂ����B(�}1(c))�B�܂��A������O��N�̓����ȏ����Ȃ�����c����Ȃ�A������c��1����菜�����ƂŋC�̂ɂ����鈳�͂�ς��邱�Ƃ��ł���B�����ŁAN�͏\���傫�Ȑ��̐����ŁA������c��1��菜�����Ƃɂ��O������C�̂ɂ����鈳�͂̕ω��ʂ͏������A�܂��C�̖̂c���ɂ��̐ϕω��ʂ��������B�ȉ��̑���α���J��Ԃ��A������c��1����菜���Ă����B ����α�F������c��1�f������菜���A�W���Î~����܂Ŗc��������
����α��k��J��Ԃ�����̗��z�C�̂̈��͂Ƒ̐ς����ꂼ��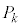 �C
�C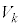 �Ƃ���B�����ŁAk��0�`N�̐����ł���A
�Ƃ���B�����ŁAk��0�`N�̐����ł���A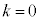 �͏��X�ɑΉ����Ă���B
�͏��X�ɑΉ����Ă���B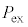 ��p�����
��p�����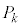 = �@���@�ł���B����α��k��s������ɂ���ɑ���α��1��s���B���̂Ƃ��C�̂�����d���́AN���\���ɑ傫���̂ŁA
= �@���@�ł���B����α��k��s������ɂ���ɑ���α��1��s���B���̂Ƃ��C�̂�����d���́AN���\���ɑ傫���̂ŁA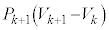 �Ƌߎ��ł���B�܂��A�����G�l���M�[�ω��́A
�Ƌߎ��ł���B�܂��A�����G�l���M�[�ω��́A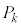 �C
�C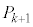 �C
�C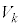 �C
�C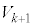 ��p����ƁA�@���@�ƕ\�����B������p���邱�ƂŁA
��p����ƁA�@���@�ƕ\�����B������p���邱�ƂŁA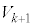 = �@���@ �~
= �@���@ �~ 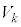 �̊W����B���삲�Ƃ̈��͕ω��Ƒ̐ϕω������ꂼ��
�̊W����B���삲�Ƃ̈��͕ω��Ƒ̐ϕω������ꂼ��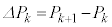 �C
�C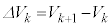 �Ƃ�����
�Ƃ����� 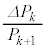 �{ �@���@ �~
�{ �@���@ �~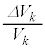 = 0
= 0�̊W����������BN���傫���Ȃ��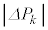 ��
��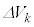 ��0�ɋ߂Â��̂ŁA����α�̌J��Ԃ��́A�C�̂̈��͂Ƒ̐ς��A���I�ɕω�������̂Ƃ݂Ȃ����Ƃ��ł��A�|�A�\���̎���������B
��0�ɋ߂Â��̂ŁA����α�̌J��Ԃ��́A�C�̂̈��͂Ƒ̐ς��A���I�ɕω�������̂Ƃ݂Ȃ����Ƃ��ł��A�|�A�\���̎���������B
���X���瑀��α��N��J��Ԃ��ƁA�S�Ă̂�����c����菜�����B�}1(c)�̏�Ԃ���J�n���āA�f�M�I�ɂ�����c��N��菜�����ꍇ�̍ŏI�I�ȋC�̂̈��͂Ƒ̐ς�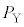 �C
�C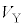 �Ƃ���B����A�}1(b)�̏�Ԃ���J�n���āA�����I�ɂ�����c��N��菜�����ꍇ�̍ŏI�I�ȋC�̂̈��͂Ƒ̐ς�
�Ƃ���B����A�}1(b)�̏�Ԃ���J�n���āA�����I�ɂ�����c��N��菜�����ꍇ�̍ŏI�I�ȋC�̂̈��͂Ƒ̐ς�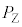 �C
�C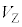 �ł���Ƃ���B
�ł���Ƃ���B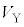 ��
��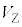 ���r�����{���F�@
���r�����{���F�@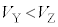 �C�A
�C�A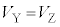 �C�B
�C�B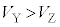 }�ł���B
}�ł���B
��1�@{��}�̑召�W�ɂ��āA���z�C�̖̂c���ɂ��d���Ɠ����G�l���M�[�ω������Ƃɐ�������B
(2) �P���q���q���z�C�̂Ƃ͈قȂ��ԕ�����������G�l���M�[�̎��ɏ]���C��F�̏�ԕω��ɂ��čl����B�������A���̋C��F�͍l���Ă��鉷�x�∳�͈͂̔͂ŋC�̂Ƃ��ĐU�镑���B�܂��A�M�͊w���@���ɏ]���A���z�C�̂Ɠ��l�ɉ��M����ƈ��͂��㏸���A�C�̂�����d���͗��z�C�̂Ɠ��l�ɕ\�����B���̋C�̂̈��́A�̐ρA�����G�l���M�[�����ꂼ��P�CV�CU�Ƃ���ƁA�C��F�ɂ���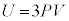 �ł��邱�Ƃ��킩���Ă���B
�ł��邱�Ƃ��킩���Ă���B �C��F�̒f�M�c�����l����B�C�̂̑̐ς�V����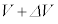 �ɔ����ω�����Ƃ��A���͂�P����
�ɔ����ω�����Ƃ��A���͂�P����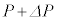 �ɁA�����G�l���M�[��U����
�ɁA�����G�l���M�[��U����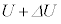 �ɁA���ꂼ������ω�����Ƃ���B�����ŁA
�ɁA���ꂼ������ω�����Ƃ���B�����ŁA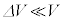 �C
�C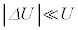 �C
�C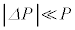 �ł���B�܂��A�ȉ��ł�
�ł���B�܂��A�ȉ��ł�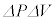 �Ȃǂ̔����ʂǂ����̐ς͖������Ă悢�B���̔����ω��ɂ��C�̂�����d�����AP�CV�C
�Ȃǂ̔����ʂǂ����̐ς͖������Ă悢�B���̔����ω��ɂ��C�̂�����d�����AP�CV�C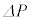 �C
�C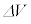 ����K�v�Ȃ��̂�p���ĕ\�����@���@�ƂȂ�B���������āA
����K�v�Ȃ��̂�p���ĕ\�����@���@�ƂȂ�B���������āA 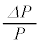 �{ �@���@ �~
�{ �@���@ �~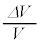 = 0
= 0��������B������A�C��F�̂������Ƃ����f�M�ω��ɂ�����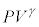 = ��� (γ = �@���@)�̊W�����藧���Ƃ��������B
= ��� (γ = �@���@)�̊W�����藧���Ƃ��������B
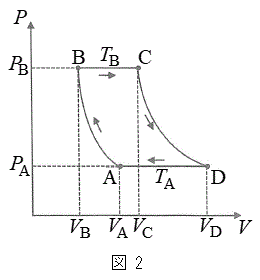 �P�ʑ̐ς�����̓����G�l���M�[�̓G�l���M�[���x�ƌĂ��B�C��F�̃G�l���M�[���x��u�ƕ\����
�P�ʑ̐ς�����̓����G�l���M�[�̓G�l���M�[���x�ƌĂ��B�C��F�̃G�l���M�[���x��u�ƕ\����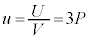 �ł���B�C��F�̃G�l���M�[���x�́A��Ή��xT�݂̂Ɉˑ���
�ł���B�C��F�̃G�l���M�[���x�́A��Ή��xT�݂̂Ɉˑ���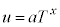 �ƕ\����邱�Ƃ��킩���Ă���B�����ŁAa��x�͐��̒萔�ł���B�C��F����ƕ����Ƃ���T�C�N�����l���邱�Ƃ�x�����߂Ă݂悤�B���̃T�C�N���ł́A�}2�Ɏ����悤�ɁA�C�̂͏��A�����B�����C�����D�����A�̂悤�ɕω����A���Ƃɖ߂�B�e�ω��́A
�ƕ\����邱�Ƃ��킩���Ă���B�����ŁAa��x�͐��̒萔�ł���B�C��F����ƕ����Ƃ���T�C�N�����l���邱�Ƃ�x�����߂Ă݂悤�B���̃T�C�N���ł́A�}2�Ɏ����悤�ɁA�C�̂͏��A�����B�����C�����D�����A�̂悤�ɕω����A���Ƃɖ߂�B�e�ω��́A ���A�����B�F�C�̂�f�M�ǂŕ������f�M�ω�
���B�����C�F��Ή��x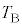 �̔M���ɋC�̂�ڐG�����������ω�
�̔M���ɋC�̂�ڐG�����������ω�
���C�����D�F�C�̂�f�M�ǂŕ������f�M�ω�
���D�����A�F��Ή��x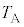 �̔M���ɋC�̂�ڐG�����������ω�
�̔M���ɋC�̂�ڐG�����������ω� �ł���B�����ŁA�e�ω��͂������Ɛi�s���A�܂��e��Ԃł̋C�̂̑̐ςƈ��͂͐}2�Ɏ����ʂ�ł���B�ȉ��ł́A���i������j�ւ̕ω��ŋC�̂������M��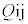 �ƕ\���B�����ŁAi��j��A�`D�̂����ꂩ���w���B
�ƕ\���B�����ŁAi��j��A�`D�̂����ꂩ���w���B
���B�̑̐�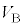 �́A
�́A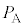 ��
��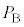 ��p�����
��p�����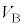 = �@���@ �~
= �@���@ �~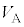 �ƂȂ�B�C��F��U��P�����łȂ�V�ɂ��ˑ����邱�Ƃɒ��ӂ���ƁA
�ƂȂ�B�C��F��U��P�����łȂ�V�ɂ��ˑ����邱�Ƃɒ��ӂ���ƁA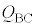 �́A
�́A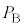 �C
�C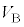 �C
�C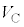 ��p����
��p����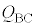 = �@���@�ƕ\�����B�܂��A
= �@���@�ƕ\�����B�܂��A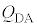 ��
��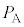 �C
�C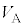 �C
�C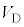 ��p���ĕ\����
��p���ĕ\����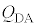 = �@���@�ƂȂ�B
= �@���@�ƂȂ�B
�������Ɛi�ޓ����ω��ƒf�M�ω�����Ȃ�T�C�N���ɂ����āA��ʂɎ��̎������m���Ă���B����(��Ή��x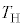 )�̔M�����瓾���M��
)�̔M�����瓾���M��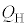 �C�ቷ(��Ή��x
�C�ቷ(��Ή��x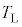 )�̔M�����瓾���M��
)�̔M�����瓾���M��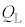 �Ƃ���ƁA
�Ƃ���ƁA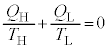 �̊W�����藧�B������C��F�̃T�C�N���ɂ��Ă͂߂��
�̊W�����藧�B������C��F�̃T�C�N���ɂ��Ă͂߂�� [ �@���@ ]�~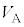 �{[ �@���@ ]�~
�{[ �@���@ ]�~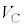 = 0
= 0 ��������(�������A�@���@���@���@��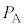 �C
�C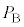 �C
�C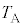 �C
�C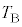 ��p���ĕ\��)�B���̎����C�ӂ�
��p���ĕ\��)�B���̎����C�ӂ�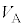 ��
��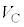 �ɂ��Đ��藧���Ƃ���x = �@���@�ƂȂ�B
�ɂ��Đ��藧���Ƃ���x = �@���@�ƂȂ�B
��2�@�C��F�̒舳������M�͒�`���邱�Ƃ��ł��Ȃ��B���̗��R���q�ׂ�B
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B