���啨��'25�N�O��[1]
���̕��͂�ǂ�ŁA�@�@�ɓK�������܂��͐��l���A{�@�@}����͓K�Ȃ��̂���I�т��̔ԍ����A���ꂼ��̉��ɋL������B�܂��A��1�ł́A�w���ɂ��������āA�����ɋL������B�������A�~������π�C�d�͉����x��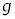 �Ƃ���B
�Ƃ���B
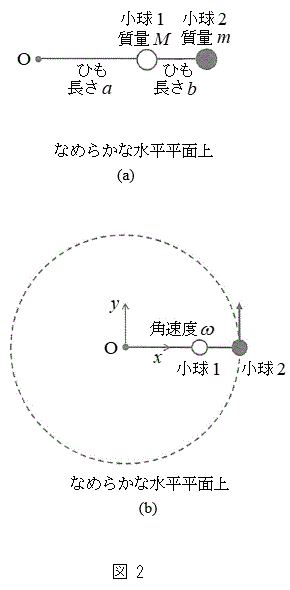
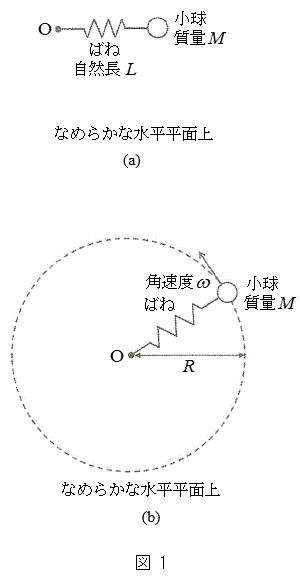 (1) �}1(a)�̂悤�Ȏ��R��L�Ŏ��ʂ������ł���˂̈�[�ɁA����M�ő傫���������ł��鏬�������t�����B���̂˂̂˒萔��k�ł���B��̂ƂȂ����˂Ə������A�Ȃ߂炩�Ȑ������ʏ�ɒu���A�������t���Ă��Ȃ����̂˂̒[���A�������ʏ�̓_O�ɌŒ肵���B�˂͓_O�̂܂������R�ɉ�]�ł���B
(1) �}1(a)�̂悤�Ȏ��R��L�Ŏ��ʂ������ł���˂̈�[�ɁA����M�ő傫���������ł��鏬�������t�����B���̂˂̂˒萔��k�ł���B��̂ƂȂ����˂Ə������A�Ȃ߂炩�Ȑ������ʏ�ɒu���A�������t���Ă��Ȃ����̂˂̒[���A�������ʏ�̓_O�ɌŒ肵���B�˂͓_O�̂܂������R�ɉ�]�ł���B�������ʏ�ŁA������_O�̂܂��ŁA������̊p���xω(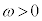 )�œ����~�^���������Ƃ��A�˂͐L�тāA�}1(b)�̂悤�ɓ_O���珬���܂ł̋�����R�ł������B�˂̕����͂ɂ�菬���ɂ͓_O�̕����֑傫���@�A�@�̗͂��������Ă���B�܂������ɂ͓_O���牓����������֑傫���@�C�@�̉��S�͂��������Ă���B���̕����֓��������̗͂̑傫���́A��������_O���珬���܂ł̋����Ɉˑ�����B���Ȃ킿�A�p���x��ω�̏ꍇ�ɁA���҂̑傫�����������Ȃ�_O���珬���܂ł̋�����R�ł���A�����k�CM�CL�Cω��p�����@�E�@�ƕ\�����B
)�œ����~�^���������Ƃ��A�˂͐L�тāA�}1(b)�̂悤�ɓ_O���珬���܂ł̋�����R�ł������B�˂̕����͂ɂ�菬���ɂ͓_O�̕����֑傫���@�A�@�̗͂��������Ă���B�܂������ɂ͓_O���牓����������֑傫���@�C�@�̉��S�͂��������Ă���B���̕����֓��������̗͂̑傫���́A��������_O���珬���܂ł̋����Ɉˑ�����B���Ȃ킿�A�p���x��ω�̏ꍇ�ɁA���҂̑傫�����������Ȃ�_O���珬���܂ł̋�����R�ł���A�����k�CM�CL�Cω��p�����@�E�@�ƕ\�����B
��1�@�}1(b)�̏������s�������~�^�����s�����߂̏����o���A�p���xω(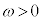 )�͈̔͂Ŏ����B
)�͈̔͂Ŏ����B
 (2) �}2(a)�̂悤�ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����a�̂Ђ��̈�[���A�Ȃ߂炩�Ȑ������ʏ�̓_O�ɌŒ肵���B�܂��A���̂Ђ��̂�������̒[�ɁA����M�ő傫���������ł��鏬��1�����t�����B����1�ɂ͂���ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����b�̂Ђ��̈�[�����t���A���̂Ђ��̑��[�ɂ͎���m�ő傫���������ł��鏬��2�����t�����B
(2) �}2(a)�̂悤�ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����a�̂Ђ��̈�[���A�Ȃ߂炩�Ȑ������ʏ�̓_O�ɌŒ肵���B�܂��A���̂Ђ��̂�������̒[�ɁA����M�ő傫���������ł��鏬��1�����t�����B����1�ɂ͂���ɁA���ʂ������ł���y���ĐL�яk�݂��Ȃ�����b�̂Ђ��̈�[�����t���A���̂Ђ��̑��[�ɂ͎���m�ő傫���������ł��鏬��2�����t�����B�͂��߁A2�̏�����2�{�̂Ђ��́A�꒼����ɘA�����ꂽ�܂܁A�Ȃ߂炩�Ȑ������ʏ�ŁA�_O�𒆐S�Ƃ���p���xω�̓����~�^�������Ă����B�}2(b)���Ɏ����ʂ�A�_O�����W���_�Ƃ��A�������ʏ�̂��������x�����A����Ɛ����ȕ�����y�����Ƃ�B��]���Ă��鏬��2�̍��W��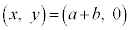 �̂Ƃ�(�}2(b))�A����a�̂Ђ����ꂽ�B�ꂽ�u�Ԃ̎�����
�̂Ƃ�(�}2(b))�A����a�̂Ђ����ꂽ�B�ꂽ�u�Ԃ̎�����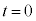 �Ƃ���B�Ȃ��ꂽ��̂Ђ��́A���̌��2�̏����̉^���ɂ͉e����^���Ȃ����̂Ƃ���B
�Ƃ���B�Ȃ��ꂽ��̂Ђ��́A���̌��2�̏����̉^���ɂ͉e����^���Ȃ����̂Ƃ���B
����b�̂Ђ��ŘA�����ꂽ2�̏����̉^���ɒ��ڂ���B�Ђ����ꂽ�����2�̏����̏d�S�̈ʒu��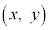 = (�@�G�@�C�@�I�@)�ł���B���̂Ƃ��d�S���猩������1�̑��Α��x�̑傫�����@�J�@�ł���A���̌�����{�L�F�@x�����̕����C�Ax�����̕����C�By�����̕����C�Cy�����̕���}�ł���B�d�S���猩������2�̑��Α��x�̑傫����������A����1�̂����Ɠ��l�ɋ��߂邱�Ƃ��ł���B����1�Ə���2��A�����钷��b�̂Ђ��ɂ������Ă��钣�͂��@�N�@�ł���A2�̏����͏d�S�܂����p���x�@�P�@�ʼn�]����B�܂��A�d�S�̉^����2�̏����̎��ʂ��d�S�ɏW���������̂Ƃ��čl���邱�Ƃ��ł���B�d�S�ɂ���������x�̑傫�����@�R�@�ł��邱�Ƃ���A�d�S��{�T�F�@�~�^���C�A�����^���C�B�P�U��}���邱�Ƃ��킩��B
= (�@�G�@�C�@�I�@)�ł���B���̂Ƃ��d�S���猩������1�̑��Α��x�̑傫�����@�J�@�ł���A���̌�����{�L�F�@x�����̕����C�Ax�����̕����C�By�����̕����C�Cy�����̕���}�ł���B�d�S���猩������2�̑��Α��x�̑傫����������A����1�̂����Ɠ��l�ɋ��߂邱�Ƃ��ł���B����1�Ə���2��A�����钷��b�̂Ђ��ɂ������Ă��钣�͂��@�N�@�ł���A2�̏����͏d�S�܂����p���x�@�P�@�ʼn�]����B�܂��A�d�S�̉^����2�̏����̎��ʂ��d�S�ɏW���������̂Ƃ��čl���邱�Ƃ��ł���B�d�S�ɂ���������x�̑傫�����@�R�@�ł��邱�Ƃ���A�d�S��{�T�F�@�~�^���C�A�����^���C�B�P�U��}���邱�Ƃ��킩��B
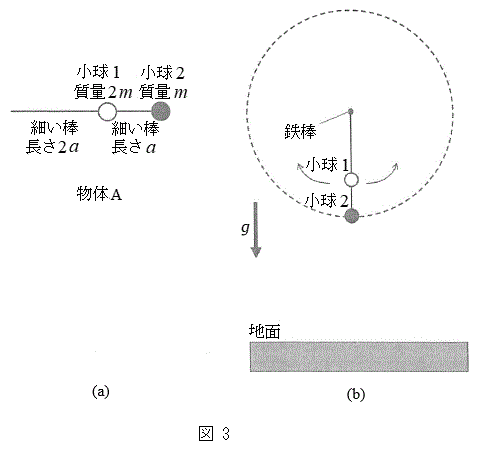 (3) �}3(a)�̂悤�ȁA���ʂ������ł���2�{�̕ό`���Ȃ��ׂ��_�ƁA�傫���������ł���2�̏������A�����ꂽ����A���쐻�����B�܂�����
(3) �}3(a)�̂悤�ȁA���ʂ������ł���2�{�̕ό`���Ȃ��ׂ��_�ƁA�傫���������ł���2�̏������A�����ꂽ����A���쐻�����B�܂�����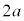 �ׂ̍��_�̈�[�Ɏ���
�ׂ̍��_�̈�[�Ɏ���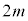 �̏���1��ڒ������B����1�ɂ͂���ɁA����a�ׂ̍��_�̈�[���Œ肵�A����ɂ��ׂ̍��_�̑��[�ɂ͎���m�̏���2���Œ肵���B����
�̏���1��ڒ������B����1�ɂ͂���ɁA����a�ׂ̍��_�̈�[���Œ肵�A����ɂ��ׂ̍��_�̑��[�ɂ͎���m�̏���2���Œ肵���B����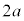 �ׂ̍��_�ƒ���a�ׂ̍��_�́A���ꂼ��̎��̉����������S�Ɉ�v���Ă���B
�ׂ̍��_�ƒ���a�ׂ̍��_�́A���ꂼ��̎��̉����������S�Ɉ�v���Ă���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�S�A���C�������Ęr�����邮��ēS�A���C����蓊���A�S�A���C����]�^��������Ƃǂ��Ȃ邩�A�Ƃ������ł��B���Ɍ����܂����A�U���ɉ����čl����Α債�����Ƃ͂���܂���B
(1) �˂̒�����R�̂Ƃ��A�˂̎��R������̐L�т�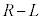 �ł��B�����ɂ͓_O�̕����֑傫��
�ł��B�����ɂ͓_O�̕����֑傫��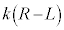 ���e�������������Ă��܂��B
���e�������������Ă��܂��B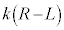 ......[�A]
......[�A] �����ɂ������Ă������S���̑傫���́A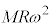 ......[�C]�e���͂Ɖ��S�͂̑傫�����������Ȃ�(�͂̂荇�����Q��)�Ƃ��A
......[�C]�e���͂Ɖ��S�͂̑傫�����������Ȃ�(�͂̂荇�����Q��)�Ƃ��A
��1�@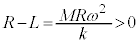 ���A
���A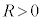 �C�܂�[�E]���A
�C�܂�[�E]���A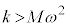 �ł���悭�A
�ł���悭�A
�� 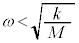
(2) 2�̏������d�S��x���W�́A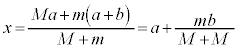 ......[�G]
......[�G] �Ђ����ꂽ����A����1������2��x����Ɉʒu����̂ŁA�d�S��y���W�́A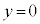 ......[�I]���̂Ƃ��A���aa�̉~�^�����s������1�̑��x��
......[�I]���̂Ƃ��A���aa�̉~�^�����s������1�̑��x��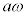 �C���a
�C���a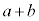 �̉~�^�����s������2�̑��x��
�̉~�^�����s������2�̑��x��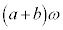 (�����~�^�����Q��)�ł��B
(�����~�^�����Q��)�ł��B
�d�S�̑��x��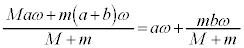
�d�S���猩������1�����Α��x�́A ���Α��x�̑傫���́A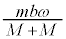 ......[�J]���Α��x�͕��Ȃ̂ŁA���̌�����y���������ł��B�C ......[�L]���l�ɁA�d�S���猩������2�̑��Α��x�́A
......[�J]���Α��x�͕��Ȃ̂ŁA���̌�����y���������ł��B�C ......[�L]���l�ɁA�d�S���猩������2�̑��Α��x�́A 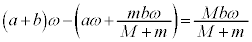 (���Ȃ̂Ō�����y���������ł�)
(���Ȃ̂Ō�����y���������ł�)�Ђ����ꂽ��A�d�S���猩������1�Ə���2�̑��x�̌����������ɂȂ邱�Ƃ���A����1�Ə���2�͏d�S�̉��ɉ~�^�����܂��B
����b�̂Ђ��ɂ������Ă��钣�͂�T�Ƃ��āA�d�S�Ə���1�̋�����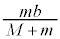 �Ȃ̂ŁA�d�S���猩������1���^���������́A
�Ȃ̂ŁA�d�S���猩������1���^���������́A 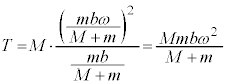 �@����@
�@����@�d�S�Ə���2�̋�����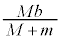 �Ȃ̂ŁA�d�S���猩������2�̉^���������́A
�Ȃ̂ŁA�d�S���猩������2�̉^���������́A 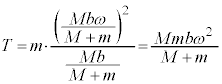 �@����A
�@����A�@�C�A������ƁA����T�ɂ��ē������ʂ�^����̂ŁA����1�Ə���2�͏d�S�̉��œ����p���xω�ʼn~�^�����邱�Ƃ��킩��܂��B����b�̂Ђ��ɂ������Ă��钣�͂́A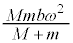 ......[�N]�C2�̏����̊p���x�́Aω ...[�P]�d�S�ɂ�����O�͂͑��݂��Ȃ��̂ŁA�d�S�ɂ���������x�̑傫���́A0 ......[�R]����āA�d�S�͓��������^�������܂��B�A ......[�T]�@(�͂̂荇�����Q��)
......[�N]�C2�̏����̊p���x�́Aω ...[�P]�d�S�ɂ�����O�͂͑��݂��Ȃ��̂ŁA�d�S�ɂ���������x�̑傫���́A0 ......[�R]����āA�d�S�͓��������^�������܂��B�A ......[�T]�@(�͂̂荇�����Q��)
(3) �S�_���珬��1�C����2�܂ł̋�����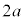 �C
�C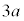 �Ȃ̂ŁA
�Ȃ̂ŁA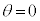 �ɂ����āA�_�ɂȂ��ꂽ����2��y������
�ɂ����āA�_�ɂȂ��ꂽ����2��y������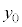 �����ƁA����1��y������
�����ƁA����1��y������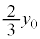 �����܂��B
�����܂��B ����2�ɏ����x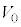 ��^����ƁA����1�̏����x��
��^����ƁA����1�̏����x��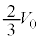 �ɂȂ�܂��B����1�Ə���2�����킹������A���^���G�l���M�[�́A
�ɂȂ�܂��B����1�Ə���2�����킹������A���^���G�l���M�[�́A 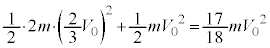 ......[�V]
......[�V]����A����]���ĉ�]�p��θ�ƂȂ����Ƃ��A����1��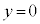 �̈ʒu����̍�����
�̈ʒu����̍�����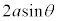 �C����2��
�C����2��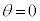 �̈ʒu����̍�����
�̈ʒu����̍�����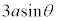 �ł��B
�ł��B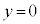 ���ʒu�G�l���M�[�̊�����Ƃ���ƁA��]�p��θ�ƂȂ����Ƃ��ɕ���A�������ʒu�G�l���M�[�́A
���ʒu�G�l���M�[�̊�����Ƃ���ƁA��]�p��θ�ƂȂ����Ƃ��ɕ���A�������ʒu�G�l���M�[�́A 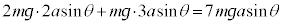 ......[�X]
......[�X]�ȉ��ł́A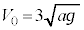 �ł��B
�ł��B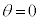 �̂Ƃ��̉^���G�l���M�[��[�V]���
�̂Ƃ��̉^���G�l���M�[��[�V]���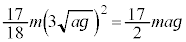 �@����B[�X]���
�@����B[�X]���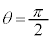 �̂Ƃ��̕���A�̈ʒu�G�l���M�[�́A
�̂Ƃ��̕���A�̈ʒu�G�l���M�[�́A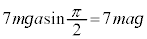 �ł��B
�ł��B
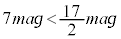 �Ȃ̂ŁA
�Ȃ̂ŁA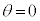 �ŕ���A�ɏ����x��^������A����A��
�ŕ���A�ɏ����x��^������A����A��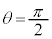 �̈ʒu�ɓ��B���܂�(�s�����~�^�����Q��)�B�܂�A����A�����߂�
�̈ʒu�ɓ��B���܂�(�s�����~�^�����Q��)�B�܂�A����A�����߂�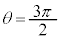 �̈ʒu�ɓ��B�����Ƃ��A����A��
�̈ʒu�ɓ��B�����Ƃ��A����A��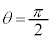 �̈ʒu��ʉ߂��Ă���A�S�_O�̐^���ɁA��������i�����Ă��܂��B�܂�A�}4(a)�̕������猩���Ƃ��ɁA����A�͔����v���ɉ�]���Ă��܂��B�A ......[�Z]����A��
�̈ʒu��ʉ߂��Ă���A�S�_O�̐^���ɁA��������i�����Ă��܂��B�܂�A�}4(a)�̕������猩���Ƃ��ɁA����A�͔����v���ɉ�]���Ă��܂��B�A ......[�Z]����A��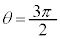 �̈ʒu�ɓ��B�����Ƃ��̕���A�̉�]�̊p���x��
�̈ʒu�ɓ��B�����Ƃ��̕���A�̉�]�̊p���x��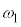 �Ƃ���ƁA���̂Ƃ��̏���1�̑�����
�Ƃ���ƁA���̂Ƃ��̏���1�̑�����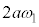 �C����2�̑�����
�C����2�̑�����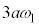 �ł��B���̂Ƃ��̕���A�̉^���G�l���M�[��
�ł��B���̂Ƃ��̕���A�̉^���G�l���M�[��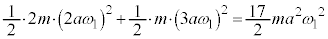 �C[�X]�ɂ���
�C[�X]�ɂ���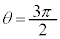 �̂Ƃ��̕���A�̈ʒu�G�l���M�[��
�̂Ƃ��̕���A�̈ʒu�G�l���M�[��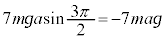
�B���A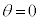 �̂Ƃ���
�̂Ƃ���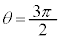 �̂Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A
�̂Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A �� 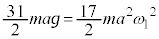 �@��
�@�� 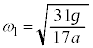 ......[�\]�A�����O��Ă���A�n�ʂɐڂ���܂ł̕���A�̗������������߂����킯�ł����A�����ɗv�������Ԃ�m��K�v������܂��B��蕶�Ɂu
......[�\]�A�����O��Ă���A�n�ʂɐڂ���܂ł̕���A�̗������������߂����킯�ł����A�����ɗv�������Ԃ�m��K�v������܂��B��蕶�Ɂu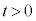 �ŏ��߂ď���2������1�̉��������ɓ��B�����Ƃ��A���傤�Ǐ���2���n�ʂɐڂ����v�Ə�����Ă���̂ł����A�A�����O�ꂽ�Ƃ��A����A�͏���2������1�̉��������ɂ���̂ŁA����2���n�ʂɐڂ���܂łɕ���A�͂��傤��1��]���Ă��邱�Ƃ��킩��܂��B��]�̊p���x��[�\]���
�ŏ��߂ď���2������1�̉��������ɓ��B�����Ƃ��A���傤�Ǐ���2���n�ʂɐڂ����v�Ə�����Ă���̂ł����A�A�����O�ꂽ�Ƃ��A����A�͏���2������1�̉��������ɂ���̂ŁA����2���n�ʂɐڂ���܂łɕ���A�͂��傤��1��]���Ă��邱�Ƃ��킩��܂��B��]�̊p���x��[�\]���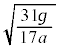 �Ȃ̂ŁA�����ɗv�������Ԃ�
�Ȃ̂ŁA�����ɗv�������Ԃ�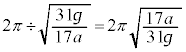 �ł��B�A���O�ꂽ�Ƃ��ƒn�ʂɐڂ����Ƃ��Ƃŕ���A�͓����p���Ȃ̂ŁA����A���������������́A�������x�^���̌������A
�ł��B�A���O�ꂽ�Ƃ��ƒn�ʂɐڂ����Ƃ��Ƃŕ���A�͓����p���Ȃ̂ŁA����A���������������́A�������x�^���̌������A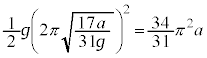 �ł��B����A�̒�����
�ł��B����A�̒�����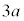 �Ȃ̂ŁA�n�ʂ���Ƃ��ēS�_�̍����́A
�Ȃ̂ŁA�n�ʂ���Ƃ��ēS�_�̍����́A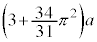 ......[�^]
......[�^]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 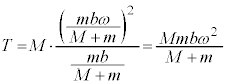 �@����@
�@����@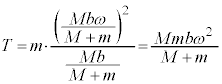 �@����A
�@����A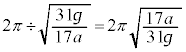 �ł��B�A���O�ꂽ�Ƃ��ƒn�ʂɐڂ����Ƃ��Ƃŕ���A�͓����p���Ȃ̂ŁA����A���������������́A�������x�^���̌������A
�ł��B�A���O�ꂽ�Ƃ��ƒn�ʂɐڂ����Ƃ��Ƃŕ���A�͓����p���Ȃ̂ŁA����A���������������́A�������x�^���̌������A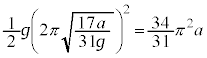 �ł��B����A�̒�����
�ł��B����A�̒�����