�@�s�����~�^��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���ar�̉~������^�����镨�̂ɓ����͂��A�~�̒��S�������Ă��Ȃ��ꍇ�������~�^�������܂���B���̂Ƃ��̉^�����A���̃T�C�g�ł́A�s�����~�^���ƌĂԂ��Ƃɂ��܂�(���K�̗p��ł͂���܂���)�B
���̂Ƃ��́A���̂�����v���p���xω �����l�ɂ͂Ȃ�܂���B
�~�̒��S�����_�ɂƂ��āAx����������̉�]�p��θ �Ƃ��܂��B���̂��ʒu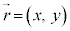 �́A���ar��萔�Ƃ��āA
�́A���ar��萔�Ƃ��āA
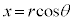 �C
�C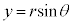
���̂����x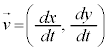 �́A
�́A
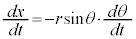 �C
�C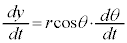
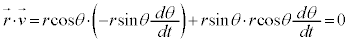
����āA���̂����x�͐ڐ������������Ă��܂��B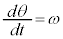 �Ə���(ω �͒萔�ł͂���܂���)�ƁA
�Ə���(ω �͒萔�ł͂���܂���)�ƁA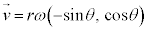 �ƂȂ�܂��B
�ƂȂ�܂��B
�����~�^���̌����F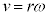 �́A�e�u�Ԃɂ����āA�s�����~�^���ł����Ă��������܂��B
�́A�e�u�Ԃɂ����āA�s�����~�^���ł����Ă��������܂��B
���̂������x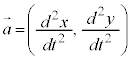 �́A
�́A
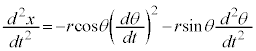 �C
�C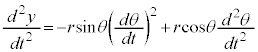
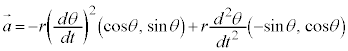
�@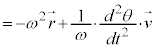
������A�����x�̓��a����(�@������)������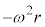 �C�ڐ�����������
�C�ڐ�����������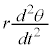 �ł��B
�ł��B
�s�����~�^�����^���������ł́A�ڐ��������l����K�v������܂��B�@�������ɓ�����(���S�����𐳂Ƃ��܂�)��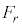 �C�ڐ������ɓ�������
�C�ڐ������ɓ�������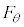 �Ƃ��āA�^���������́A
�Ƃ��āA�^���������́A
�@�������ɂ��āA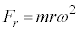 (
(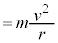 )
)
�ڐ������ɂ��āA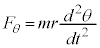
�@�������̉^���������́A�����~�^���̏ꍇ�Ɠ����ł��B�ڐ������̉^���������͈�ʓI�ɂ͉����Ȃ��̂ŁA����ɑ�����̂��l���܂��B
�������ł́A���C�Ȃǂ������͊w�I�G�l���M�[�ۑ�������������Ŗ����l����ꍇ���قƂ�ǂł��B���̂Ƃ��ɂ́A
| �s�����~�^���̖��́A�@�������̉^��������(�����~�^���Ɠ���)�Ɨ͊w�I�G�l���M�[�ۑ�����A�� |
���邱�Ƃɂ���āA�����܂��B��w�����ł͕p�o�Ȃ̂Ŋo���Ă����Ă��������B
���C���l����ꍇ�ł��A���C���̂����d�����l�����G�l���M�[�̎��𗧂Ă�A�����ł���悤�ɂȂ��Ă���͂��ł��B
[��1]�@����r�̌y�������_�̈�[������m�̂�����������[�𒆐S�ɁA�����ʓ��ʼn�]�����܂��B�ō��_��ʉ߂��邽�߂́A�ʼn��_�ɂ���������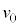 �Ɋւ�����������߂܂��B�d�͉����x��
�Ɋւ�����������߂܂��B�d�͉����x��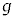 �Ƃ��܂��B
�Ƃ��܂��B
�ō��_�ł�������v�Ƃ��āA�ʼn��_�ƍō��_�ł̗͊w�I�G�l���M�[�ۑ����A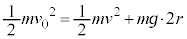
�ō��_��ʉ߂�������́A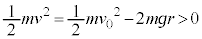
�� 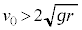
[��2]�@����r�̌y�����̈�[������m�̂�����������[�𒆐S�ɁA�����ʓ��ʼn�]�����܂��B��������ނ��ƂȂ��ō��_��ʉ߂��邽�߂́A�ʼn��_�ɂ���������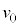 �Ɋւ�����������߂܂��B�d�͉����x��
�Ɋւ�����������߂܂��B�d�͉����x��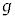 �Ƃ��܂��B
�Ƃ��܂��B
���̏ꍇ�ɂ́A�����ł��܂����Ƃ�����̂ŁA[��1]�̗͊w�I�G�l���M�[�ۑ��ɕt�������āA��������T���l����K�v������܂��B
�͊w�I�G�l���M�[�ۑ��͗�1�Ɠ������A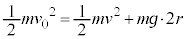 ����@
����@
�ō��_�ɂ����鎅��������T�Ƃ��āA�ō��_�ł̉^���������́A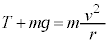 ����A
����A
�@���A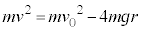
�A�ɑ������ƁA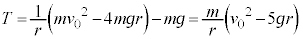
�ō��_�ł���������܂Ȃ������́A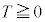 (�o���Ă�������)
(�o����������)
�� 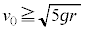
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 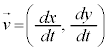 �́A
�́A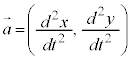 �́A
�́A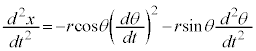 �C
�C