京大物理'25年前期[2]
次の文章を読んで、 に適した式または数値を、{ }からは適切なものを一つ選びその番号を、それぞれの解答欄に記入せよ。なお、 はすでに で与えられたものと同じものを表す。また、問1~問3では、指示にしたがって、解答をそれぞれの解答欄に記入せよ。ただし、円周率をπとし、以下に登場する物質や気体の透磁率はすべてμとする。
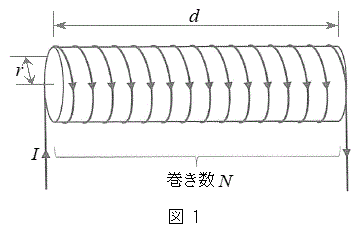 (1) 図1のように、長さd,半径rの円筒に抵抗の無視できる導線を一様にN回巻き付けて作ったソレノイド(以下コイルと呼ぶ)がある。円筒内部は気体で満たされており、コイルの長さdはrと比べて十分長く、このコイルに電流を流すと円筒内部には一様な磁束密度ができる。このコイルに外部電源を接続して電流Iを流したときに円筒内部に発生する磁束密度の大きさは イ である。
(1) 図1のように、長さd,半径rの円筒に抵抗の無視できる導線を一様にN回巻き付けて作ったソレノイド(以下コイルと呼ぶ)がある。円筒内部は気体で満たされており、コイルの長さdはrと比べて十分長く、このコイルに電流を流すと円筒内部には一様な磁束密度ができる。このコイルに外部電源を接続して電流Iを流したときに円筒内部に発生する磁束密度の大きさは イ である。次に、微小時間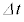 の間に電流をIから
の間に電流をIから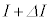 にゆっくり変化させると、コイルには誘導起電力 ロ ×
にゆっくり変化させると、コイルには誘導起電力 ロ ×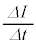 が発生する(
が発生する(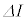 は微小量であり、起電力の符号は電流の上流側の電位が高い場合を正とする)。このことから、このコイルの自己インダクタンスは ハ である。また、時間
は微小量であり、起電力の符号は電流の上流側の電位が高い場合を正とする)。このことから、このコイルの自己インダクタンスは ハ である。また、時間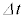 の間に外部電源がコイルにした仕事は ニ ×
の間に外部電源がコイルにした仕事は ニ ×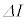 である。
である。
図1のコイルに電流Iが流れているとき、コイルにはエネルギー ホ が蓄えられている。コイルを流れる電流がIから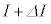 に変化する際のこのエネルギーの増加は、
に変化する際のこのエネルギーの増加は、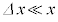 を満たす十分小さな
を満たす十分小さな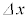 に対して成立する近似式
に対して成立する近似式 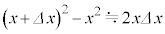 ・・・(i)
・・・(i)を使うと ニ ×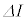 となり、外部電源がコイルにした仕事と一致する。つまり、外部電源が行った仕事がコイルのエネルギーとして蓄積される。
となり、外部電源がコイルにした仕事と一致する。つまり、外部電源が行った仕事がコイルのエネルギーとして蓄積される。
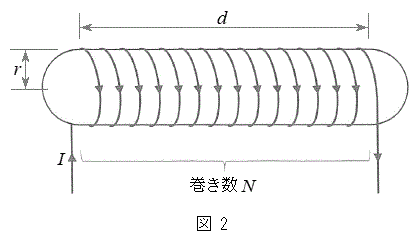 (2) 図2のように、バルーンアート用の風船のような細長い円筒形状をした伸縮自在の閉じた膜に、伸縮自在で抵抗の無視できる導線を巻き数密度(円筒軸方向の単位長さ当たりの導線の本数)が一様となるようにN回巻き付けて作ったソレノイド(以下コイルと呼ぶ)がある。膜内部の気体の量は調整でき、このとき膜は円筒形状を保ったまま半径や長さが変わる。導線は膜に接着されており、膜の半径や長さが変化するとき導線は膜に接したままむらなく伸び縮みし、巻き数密度は一様に保たれるものとする。また、膜は厚みの無視できる絶縁体でできており、膜と導線は容易に伸縮するものとし、膜の面積、導線の長さおよび形状の変化に要する仕事は十分小さく無視できるものとする。
(2) 図2のように、バルーンアート用の風船のような細長い円筒形状をした伸縮自在の閉じた膜に、伸縮自在で抵抗の無視できる導線を巻き数密度(円筒軸方向の単位長さ当たりの導線の本数)が一様となるようにN回巻き付けて作ったソレノイド(以下コイルと呼ぶ)がある。膜内部の気体の量は調整でき、このとき膜は円筒形状を保ったまま半径や長さが変わる。導線は膜に接着されており、膜の半径や長さが変化するとき導線は膜に接したままむらなく伸び縮みし、巻き数密度は一様に保たれるものとする。また、膜は厚みの無視できる絶縁体でできており、膜と導線は容易に伸縮するものとし、膜の面積、導線の長さおよび形状の変化に要する仕事は十分小さく無視できるものとする。なお、以下では必要に応じて近似式(i)を使って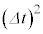 を無視し、解答欄には
を無視し、解答欄には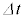 を使わずに解答を記入せよ。
を使わずに解答を記入せよ。
まず、コイルの両端を固定装置で固定して動かないようにし、膜の長さがdに保たれるようにした。この状態でコイルに電流Iを流し、膜内部の気体の量を調整して、図2のようにコイルの半径がrとなる状態を作った。このとき、コイル内部には一様な磁束密度 イ が発生した。この状態から、電流Iを一定に保ったまま膜内部の気体の量をゆっくり増加させたところ、コイルの半径は速さvで大きくなり、微小時間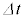 ののちに
ののちに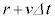 になった。このとき、コイル一巻きを貫く磁束は
になった。このとき、コイル一巻きを貫く磁束は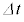 の間に
の間に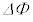 = ヘ ×
= ヘ ×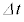 だけ増加するので、コイルには誘導起電力 ト が発生する(起電力の符号は電流の上流側の電位が高いときを正とする)。また、時間
だけ増加するので、コイルには誘導起電力 ト が発生する(起電力の符号は電流の上流側の電位が高いときを正とする)。また、時間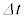 の間に外部電源がコイルに対して行う仕事は チ ×
の間に外部電源がコイルに対して行う仕事は チ ×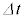 である。
である。
一方、コイルに蓄えられるエネルギー( ホ )は、コイル半径が大きくなったことにより時間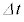 の間に リ ×
の間に リ ×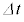 だけ増加する。このエネルギーの変化は、外部電源が行った仕事 チ と、膜内外の気体の圧力差が膜に対して行った仕事の和に等しい。時間
だけ増加する。このエネルギーの変化は、外部電源が行った仕事 チ と、膜内外の気体の圧力差が膜に対して行った仕事の和に等しい。時間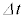 の間にコイルの体積は ヌ ×
の間にコイルの体積は ヌ ×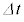 だけ増加するので、膜内外の圧力差を
だけ増加するので、膜内外の圧力差を 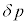 = (外部の気体の圧力)-(内部の気体の圧力)
= (外部の気体の圧力)-(内部の気体の圧力)とすると、膜内外の気体の圧力差が時間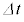 の間にに膜に対して行う仕事は
の間にに膜に対して行う仕事は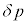 を使って ル ×
を使って ル ×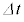 と書ける。以上のことから膜内外の気体の圧力差
と書ける。以上のことから膜内外の気体の圧力差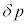 を求めることができ、μと イ で求めたコイル内部の磁束密度Bのみを用いて表すと
を求めることができ、μと イ で求めたコイル内部の磁束密度Bのみを用いて表すと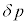 = ヲ と書ける。
= ヲ と書ける。
いま、膜には膜内外の気体がもたらす圧力差に加え、電流Iが作り出す圧力が働いている。これらの圧力がつり合いの条件を満たすことから、電流Iが作り出す圧力は、{ワ:①コイルを膨らませる方向に働いている,②コイルを収縮させる方向に働いている,③働いていない}。
(3) コイルを図2の状態に戻してから、コイルの半径をrに固定したうえでコイルの円筒軸方向の長さを自由に変化させられるようにした。コイルの円筒軸方向長さがdの状態から、電流Iを一定に保ったまま膜の内部の気体量を変化させたところ、円筒軸方向の長さが速さvでゆっくりと大きくなり、微小時間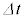 ののちに
ののちに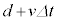 になった。このとき、
になった。このとき、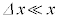 を満たす十分小さな
を満たす十分小さな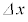 に対して成り立つ近似式
に対して成り立つ近似式 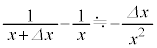 ・・・(ii)
・・・(ii)を使って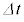 の2次以上の項を無視すると、微小時間
の2次以上の項を無視すると、微小時間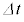 の間に外部電源がコイルに対して行う仕事は カ ×
の間に外部電源がコイルに対して行う仕事は カ ×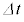 であることが分かる。このとき問1~問3に答えよ。
であることが分かる。このとき問1~問3に答えよ。
問1 膜内外の気体の圧力差を
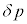 = (外部の気体の圧力)-(内部の気体の圧力)
= (外部の気体の圧力)-(内部の気体の圧力)とするとき、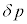 を求めよ。ただし、近似式(ii)を使って
を求めよ。ただし、近似式(ii)を使って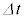 の2次以上の項を無視し、解答にはμと イ で求めたコイル内部の磁束密度Bのみを用いよ。
の2次以上の項を無視し、解答にはμと イ で求めたコイル内部の磁束密度Bのみを用いよ。
問2 電流Iがコイルの両端面に作り出す圧力の向きについて、適切なものを以下から選んで番号を解答欄に記入せよ。
① コイルが円筒軸方向に伸びようとする圧力が働いている。
② コイルが円筒軸方向に縮もうとする圧力が働いている。
③ 圧力は働いていない。
問3 問2の結果を、コイルを形成する各一巻きの導線を流れる電流が相互に及ぼす力について簡潔に説明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 出題者としては親切のつもりで付けた「起電力の符号は電流の上流側の電位が高い場合を正とする」という指定を誤解した受験生がいたかも知れません。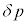 を
を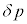 = (外部の気体の圧力)-(内部の気体の圧力)としていることにも注意が必要です。円筒内部の気体が外部に対してする仕事は、
= (外部の気体の圧力)-(内部の気体の圧力)としていることにも注意が必要です。円筒内部の気体が外部に対してする仕事は、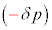 ×(気体の体積増加)です。
×(気体の体積増加)です。
(1) コイルの単位長さあたりの巻数は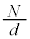 なので、電流Iを流したときに円筒内部に発生する磁場の強さHは(電流の作る磁界を参照)、
なので、電流Iを流したときに円筒内部に発生する磁場の強さHは(電流の作る磁界を参照)、
円筒内部に発生する磁束密度の大きさBは、透磁率μより、
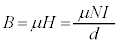 ......[イ]
......[イ]微小時間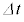 の間に電流をIから
の間に電流をIから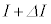 に変化させたときコイルに発生する誘導起電力Vは、コイルの断面積が
に変化させたときコイルに発生する誘導起電力Vは、コイルの断面積が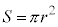 であることから、
であることから、 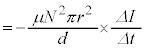 ・・・①
・・・①起電力は、電流Iと逆向きに電流を流そうとする向き(レンツの法則を参照)で、「起電力の符号は電流の上流側の電位が高い場合を正とする」という注意書きより、電流の上流側の電位が高く、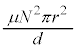 ......[ロ]自己インダクタンスをLとして、コイルの電圧
......[ロ]自己インダクタンスをLとして、コイルの電圧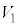 は、
は、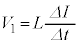 (自己誘導を参照)より、
(自己誘導を参照)より、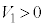 ,
,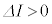 に注意して、
に注意して、 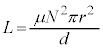 ......[ハ]
......[ハ]時間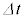 の間に外部電源がコイルにした仕事は、
の間に外部電源がコイルにした仕事は、 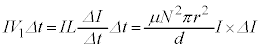
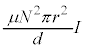 ......[ニ]
......[ニ]電流Iが流れるコイルに蓄えられるエネルギーは、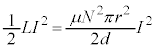 ......[ホ]コイルに流れる電流がIから
......[ホ]コイルに流れる電流がIから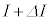 に変化する際のエネルギーの増加は、近似式(i)と[ハ]の結果を用いて、
に変化する際のエネルギーの増加は、近似式(i)と[ハ]の結果を用いて、 となり、外部電源がコイルにした仕事[ニ]×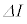 に一致します。
に一致します。
(2) [イ]と同様に磁束密度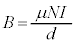 ,磁束
,磁束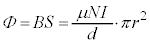 が発生し、膜内部の気体の量を増加させ、コイルの半径が微小時間
が発生し、膜内部の気体の量を増加させ、コイルの半径が微小時間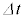 の間に
の間に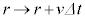 となると、磁束の変化
となると、磁束の変化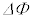 は、近似式(i)を用いて、
は、近似式(i)を用いて、 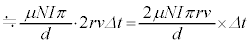
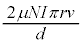 ......[へ]
......[へ]コイルに発生する起電力は、
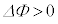 より磁束が増加するので、起電力の向きはこれを打ち消そうとする向き(左向きの磁界を作る向きで、電流を矢印と逆向きに流そうとする向き)で、電流の上流側の電位が高く、起電力は正で、
より磁束が増加するので、起電力の向きはこれを打ち消そうとする向き(左向きの磁界を作る向きで、電流を矢印と逆向きに流そうとする向き)で、電流の上流側の電位が高く、起電力は正で、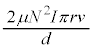 ......[ト]
......[ト]コイルの電圧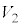 は
は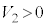 で、
で、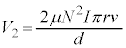 より、時間
より、時間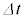 の間に外部電源がコイルに対して行う仕事は
の間に外部電源がコイルに対して行う仕事は 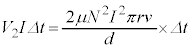
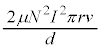 ......[チ]
......[チ]コイルに蓄えられるエネルギー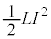 の変化は、コイルの半径が大きくなったことにより、近似式(i)と[ホ]の結果を用いて、
の変化は、コイルの半径が大きくなったことにより、近似式(i)と[ホ]の結果を用いて、 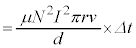
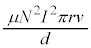 ......[リ]
......[リ]コイルの体積増加は、
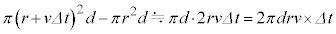
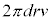 .......[ヌ]
.......[ヌ]であり、気体の圧力差が行った仕事は、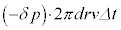
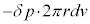 ......[ル]コイルに蓄えられるエネルギーの増加分[リ]×
......[ル]コイルに蓄えられるエネルギーの増加分[リ]×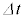 を、外部電源の行った仕事[チ]×
を、外部電源の行った仕事[チ]×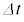 と気体の圧力差が行った仕事[ル]×
と気体の圧力差が行った仕事[ル]×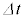 の和に等しいとおくと、
の和に等しいとおくと、 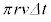 で割り、
で割り、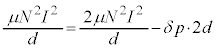
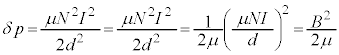 ......[ヲ]
......[ヲ]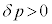 ということは、外部の気体の圧力が内部の気体の圧力よりも大きい、ということであり、円筒膜はしぼんでしまいます。しぼむことがないので、この圧力とつり合うように、電流Iが作り出す圧力が働き、電流Iが作り出す圧力はコイルを膨らませる方向に働いています。① ......[ワ]
ということは、外部の気体の圧力が内部の気体の圧力よりも大きい、ということであり、円筒膜はしぼんでしまいます。しぼむことがないので、この圧力とつり合うように、電流Iが作り出す圧力が働き、電流Iが作り出す圧力はコイルを膨らませる方向に働いています。① ......[ワ]
(3) 磁束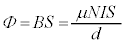 において、コイルの円筒軸方向の長さを
において、コイルの円筒軸方向の長さを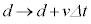 とすると、磁束の変化
とすると、磁束の変化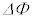 は、近似式(ii)を用いて、
は、近似式(ii)を用いて、 微小時間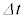 の間に生じる誘導起電力は
の間に生じる誘導起電力は 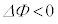 で磁束が減るので、右向きの磁界を作る向きの起電力が生じ、コイルの右側が高電位になります。コイルの電圧
で磁束が減るので、右向きの磁界を作る向きの起電力が生じ、コイルの右側が高電位になります。コイルの電圧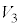 は
は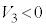 であり
であり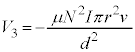 となります。これより、微小時間
となります。これより、微小時間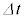 の間に外部電源がコイルに対してする仕事は、
の間に外部電源がコイルに対してする仕事は、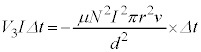
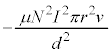 ......[カ]
......[カ]
問1 コイルのエネルギー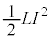 の変化は、近似式(ii)と[ホ]の結果を用いて、
の変化は、近似式(ii)と[ホ]の結果を用いて、
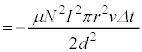 ・・・②
・・・②円筒状膜の体積変化は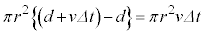
気体の圧力差がした仕事は、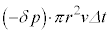 ・・・③
・・・③
コイルのエネルギーの変化②を、外部電源の行った仕事[カ]×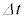 と気体の圧力差が行った仕事③の和に等しいとして、
と気体の圧力差が行った仕事③の和に等しいとして、 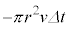 で割ると、
で割ると、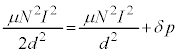
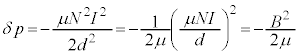 ......[答]
......[答]
問2 [ワ]とは異なり、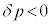 なので、内部圧力が外部圧力よりも大きい、ということです。ということは、これとつり合うように働く圧力、つまり、電流が作り出す圧力は、コイルが円筒軸方向に縮もうとする方向に働きます。② ......[答]
なので、内部圧力が外部圧力よりも大きい、ということです。ということは、これとつり合うように働く圧力、つまり、電流が作り出す圧力は、コイルが円筒軸方向に縮もうとする方向に働きます。② ......[答]
問3 コイル上で隣接する導線には同一方向に電流が流れるので、電流相互に引力が働く。 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
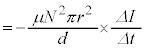 ・・・①
・・・①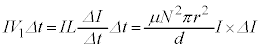
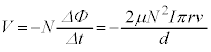
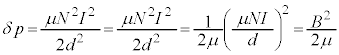 ......[ヲ]
......[ヲ]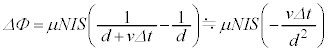
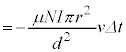
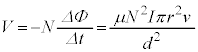
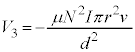 となります。これより、微小時間
となります。これより、微小時間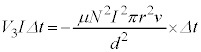
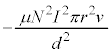 ......[カ]
......[カ]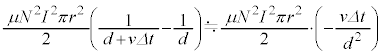
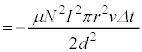 ・・・②
・・・②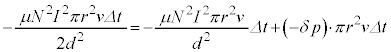
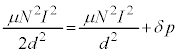
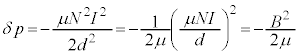 ......[答]
......[答]