����`��R�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�d�����d���̊W��\���O���t�������ɂȂ�Ȃ���R������`��R�ƌ����B
���x�ˑ�����L�����R�̂̏ꍇ�A��R���g�����M�̂��߂ɁA��R�l���d���ɂ���ĕω����A�d�����d���ɔ�Ⴕ�Ȃ��Ȃ�܂��B�d�����d����1�����ŕ\���Ȃ���R������`��R�ƌ����܂�(���D�u���`�v�Ƃ����̂͒�R�̂̌`��������̂ł͂Ȃ��A�d�����d���̊W�̃O���t�������ɂȂ�Ȃ��A�Ƃ����Ӗ��ł�)�B
����`��R�ł��I�[���̖@���͐������܂���B
�d���A�T�[�~�X�^�A�_�C�I�[�h�A�g�����W�X�^�Ȃǂ̓d�C���i������`��R�ł��B
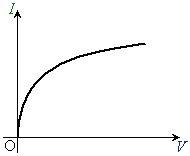 ����`��R�ł́A�d�����d���̊��Ƃ��ĕ\���ꂸ�A���̃O���t(�����Ȑ��ƌ����܂��B���ʁA�d�������c���A�d�����������Ɏ���ăO���t�������܂�)�������^�����Ă��āA��H�̌v�Z���s���K�v������܂��B���邢�́A�d�����d���̊W�����^�����Ă��Ă��A�����I�ɉ������Ƃ���������肵�܂��B�����ł́A�E�}�̂悤�ȁA�d�����d���̊W�ł���d�����^�����Ă����Ƃ��܂��B
����`��R�ł́A�d�����d���̊��Ƃ��ĕ\���ꂸ�A���̃O���t(�����Ȑ��ƌ����܂��B���ʁA�d�������c���A�d�����������Ɏ���ăO���t�������܂�)�������^�����Ă��āA��H�̌v�Z���s���K�v������܂��B���邢�́A�d�����d���̊W�����^�����Ă��Ă��A�����I�ɉ������Ƃ���������肵�܂��B�����ł́A�E�}�̂悤�ȁA�d�����d���̊W�ł���d�����^�����Ă����Ƃ��܂��B
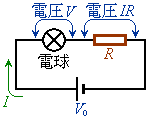 ���̓d������RR��ɐڑ����A�N�d��
���̓d������RR��ɐڑ����A�N�d��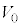 �̓d�r�ɐڑ������Ƃ��܂��B
�̓d�r�ɐڑ������Ƃ��܂��B
�L���q�z�b�t��2�@�����A�d�����[���d����V�Ƃ��āA
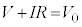 �@����@
�@����@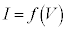 �̂悤�Ɏ��ŗ^����ꂽ�Ƃ���A���̎��Ƈ@����A������Γd���𗬂���d��I���d��V�����߂邱�Ƃ��ł��܂��B
�̂悤�Ɏ��ŗ^����ꂽ�Ƃ���A���̎��Ƈ@����A������Γd���𗬂���d��I���d��V�����߂邱�Ƃ��ł��܂��B
�A���������������A�Ƃ����̂͂ǂ��������Ƃ��ƌ����ƁA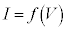 �̃O���t�Ƈ@���̃O���t�̌�_�����߂�Ƃ������Ƃł��B
�̃O���t�Ƈ@���̃O���t�̌�_�����߂�Ƃ������Ƃł��B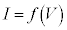 �̃O���t�͊��ɗ^�����Ă���̂ŁA�@���̃O���t����������ŁA��_�����߂�A�A���������̉��ł���I��V�����߂邱�Ƃ��ł���͂��ł��B
�̃O���t�͊��ɗ^�����Ă���̂ŁA�@���̃O���t����������ŁA��_�����߂�A�A���������̉��ł���I��V�����߂邱�Ƃ��ł���͂��ł��B
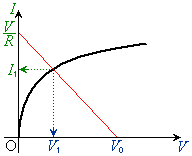 �@���̃O���t�͒����ł��B
�@���̃O���t�͒����ł��B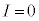 �Ƃ����
�Ƃ����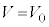 �C
�C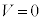 �Ƃ����
�Ƃ����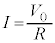 �ƂȂ�̂ŁA�@���̃O���t�́A
�ƂȂ�̂ŁA�@���̃O���t�́A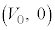 �C
�C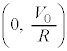 ��2�_��ʂ钼���ŁA�����ɒ������������Ƃ��ł��܂��B�������ĉE�}�̂悤�ɁA���̒�����
��2�_��ʂ钼���ŁA�����ɒ������������Ƃ��ł��܂��B�������ĉE�}�̂悤�ɁA���̒�����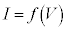 �̃O���t�Ƃ̌�_
�̃O���t�Ƃ̌�_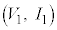 �̒l��ǂݎ��A�A���������̉��́A
�̒l��ǂݎ��A�A���������̉��́A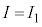 �C
�C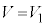 �ł���A�d���𗬂���d����
�ł���A�d���𗬂���d����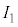 �C�d�����[���d����
�C�d�����[���d����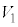 �Ƃ������ƂɂȂ�܂��B
�Ƃ������ƂɂȂ�܂��B
�L���q�z�b�t�̖@������o�Ă����d�����d���̊W�́A��R�Ɠd�r��������Ȃ��H�ł́A1�����ɂȂ�̂ŁA���̃O���t�͒����ł��B����`��R���͂̉�H����R�Ɠd�r�����łł��Ă���A����`��R�̃O���t���ǂ̂悤�Ȃ��̂ł����Ă��A��L�̂悤�ɂ��āA�O���t��p���Ĕ���`��R�𗬂���d�����d���̒l�����߂邱�Ƃ��ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 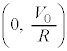 ��2�_��ʂ钼���ŁA�����ɒ������������Ƃ��ł��܂��B�������ĉE�}�̂悤�ɁA���̒�����
��2�_��ʂ钼���ŁA�����ɒ������������Ƃ��ł��܂��B�������ĉE�}�̂悤�ɁA���̒�����