�����̊����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
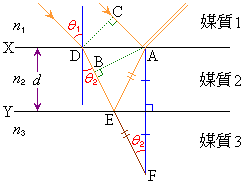
���@��������Ƃ��ɁA�X�v���[�𐁂������Ă����ƈ�@������ƁA�K���X�\�ʂ��F�Â��Č����邱�Ƃ�����܂��B���̌����́A�E�}�̂悤�ɁA�K���X�\�ʂɂł��Ă��锖�����̏�ʂŔ��˂������Ɖ��ʂŔ��˂������Ƃ������āA����̔g���̌������ߍ�������ł��B
 �E�}�̂悤�ɁA���ܗ�
�E�}�̂悤�ɁA���ܗ�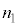 �̔}��1�A���ܗ�
�̔}��1�A���ܗ�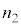 �̔}��2�A���ܗ�
�̔}��2�A���ܗ�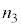 �̔}��3���A���E��X�C���E��Y�Őڂ��Ă���Ƃ��܂��B���E��X�Ƌ��E��Y�͕��s�ȕ��ʂŁA�}��2�̕����������A�܂苫�E��X�Ƌ��E��Y��������d���Ƃ��܂��B
�̔}��3���A���E��X�C���E��Y�Őڂ��Ă���Ƃ��܂��B���E��X�Ƌ��E��Y�͕��s�ȕ��ʂŁA�}��2�̕����������A�܂苫�E��X�Ƌ��E��Y��������d���Ƃ��܂��B
�}��1��ʉ߂��Ă����g��λ�̌������E��X�ɓ��ˊp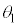 �œ��˂��A�ꕔ�̌��͔��˂��Ĕ}��1�̒��ɖ߂�A�ꕔ�̌��͔}��2�̒����܂��ē��荞�݂܂��B���̂Ƃ��̋��܊p��
�œ��˂��A�ꕔ�̌��͔��˂��Ĕ}��1�̒��ɖ߂�A�ꕔ�̌��͔}��2�̒����܂��ē��荞�݂܂��B���̂Ƃ��̋��܊p��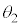 �Ƃ���ƁA���܂̖@�����A
�Ƃ���ƁA���܂̖@�����A
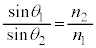 �@����@
�@����@
�E�}�_D�Ŕ}��2�ɓ��荞���́A���E��Y��̓_E���������A���E��X��̓_A�ɗ��܂��B�_A�Ň@�����悤�ɍēx���܂��A�}��1��ʉ߂��_A������������Əd�Ȃ�܂��B����2�����������N�����܂��B
�����ċ��ߍ��������́A���H��(�����ł́A�}��1�Ɣ}��2�̋��ܗ����قȂ�̂ŁA�o�H���ł͂Ȃ��A�o�H���ɋ��ܗ������������H���ōl���܂�)���A�g���Ƃǂ������W�������A�Ƃ������ƂŌ��܂�܂��B�����ł́A���H�����ǂ��Ȃ邩�A�Ƃ������ƂƁA2�����ʑ��̊W��2�_�ɂ��čl���Ȃ�������܂���B
�܂��A���H�����l���܂��B�E�}�Œ���CD��ł́A2���͔g�ʂ��`�����A�ʑ��͑����Ă��܂��B�Е���C����A�܂ŗ���ԂɁA�}��2�̒��֓��荞���́AD����B�܂Ői�݂܂��B�i���������Ⴄ�̂́A���ܗ����قȂ���̐i���������قȂ邩��ł��B�E�}�ł́A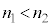 �̏�z�肵�āA
�̏�z�肵�āA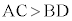 �ƂȂ�悤�ɕ`���Ă���܂��B�}��2�̒��֓��荞���́A�o�H��
�ƂȂ�悤�ɕ`���Ă���܂��B�}��2�̒��֓��荞���́A�o�H��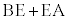 �����]����������i�ނ��ƂɂȂ�܂��B
�����]����������i�ނ��ƂɂȂ�܂��B
���E��Y�Ŕ��˂���̂ŁA�_E�ɂ��������������̔��˂̂悤�ɁA�����Œ��i���ċ��E��Y�Ɋւ���A�̑Ώ̓_F�Ɍ������Đi�ނƍl����ƁA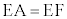 �C
�C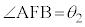 ���A�o�H���́A
���A�o�H���́A
�ƂȂ�܂��B�}��2�̋��ܗ���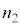 �Ȃ̂ŁA���H�����o�H����
�Ȃ̂ŁA���H�����o�H����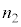 �������āA
�������āA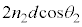 �ƂȂ�܂��B
�ƂȂ�܂��B
���ɁA�_A�C�_B�ɂ����������̏��l���܂��B�_A�ł̔��˂́A���ܗ�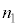 �̔}��������ܗ�
�̔}��������ܗ�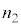 �̔}���ɓ��荞�����Ƃ��ċN���锽�˂ł��B
�̔}���ɓ��荞�����Ƃ��ċN���锽�˂ł��B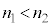 �ł���A���̔��˂��Œ�[�̔����ƂȂ�A�����ʑ���π����܂��B�܂�A���g��������܂��B
�ł���A���̔��˂��Œ�[�̔����ƂȂ�A�����ʑ���π����܂��B�܂�A���g��������܂��B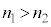 �ł���A���̔��˂����R�[�̔����ł��B�����ʑ��͂���܂���B�_E�ł̔��˂����l�ɁA
�ł���A���̔��˂����R�[�̔����ł��B�����ʑ��͂���܂���B�_E�ł̔��˂����l�ɁA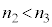 �ł���ΌŒ�[�̔��˂Ō����ʑ���π����A
�ł���ΌŒ�[�̔��˂Ō����ʑ���π����A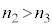 �ł���Ύ��R�[�̔��˂��ʑ��͂���܂���B
�ł���Ύ��R�[�̔��˂��ʑ��͂���܂���B
�]���āA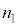 �C
�C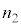 �C
�C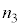 �̑召�W�ɂ���āA2�����ʑ��̊W���A���g�����ꂽ��A����Ȃ������肵�܂��B2�̏ɂ����čl���Ă݂邱�Ƃɂ��܂��B
�̑召�W�ɂ���āA2�����ʑ��̊W���A���g�����ꂽ��A����Ȃ������肵�܂��B2�̏ɂ����čl���Ă݂邱�Ƃɂ��܂��B
��1�F�K���X�\�ʂɁA�K���X�������ܗ��̏����Ȕ��������Ă��āA��C��������������ɓ��˂���Ƃ��́A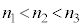 �ƂȂ�̂ŁA�_A�ł��_E�ł��Œ�[�̔��˂ŁA2���Ƃ��ʑ���π�����̂ŁA2���̊Ԃɂ��ʑ��̂���͂���܂���B
�ƂȂ�̂ŁA�_A�ł��_E�ł��Œ�[�̔��˂ŁA2���Ƃ��ʑ���π�����̂ŁA2���̊Ԃɂ��ʑ��̂���͂���܂���B ��2�F�K���X�\�ʂɁA�K���X�������ܗ��̑傫�Ȕ��������Ă��āA��C��������������ɓ��˂���Ƃ��́A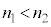 �C
�C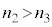 �ƂȂ�̂ŁA�_A�ł͌Œ�[�̔��˂ł����A�_E�ł͎��R�[�̔��˂ƂȂ�A�_A�ł̔��˂̂��ʑ���π�����̂ŁA2���̊Ԃ��ʑ������g��������邱�ƂɂȂ�܂��B�V���{���ʂ����̖A�̕\�ʂ��F�Â��Č�����悤�ȏꍇ���A���̏ɂȂ�܂��B
�ƂȂ�̂ŁA�_A�ł͌Œ�[�̔��˂ł����A�_E�ł͎��R�[�̔��˂ƂȂ�A�_A�ł̔��˂̂��ʑ���π�����̂ŁA2���̊Ԃ��ʑ������g��������邱�ƂɂȂ�܂��B�V���{���ʂ����̖A�̕\�ʂ��F�Â��Č�����悤�ȏꍇ���A���̏ɂȂ�܂��B ��1��2���̊Ԃ��ʑ��̂��ꂪ�Ȃ��ꍇ�ɁA2���������������ߍ��������́A���H�����g���̐����{�ƂȂ邱�ƂŁA 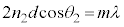 �@(
�@(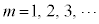 )�@����A
)�@����A��2��2���̊Ԃ����g�����̂��ꂪ�����Ă���ꍇ�ɂ́A2�������ߍ��������́A���H�����g���̐����{�������g������邱�ƂŁA
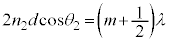 �@(
�@(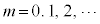 )�@����B
)�@����B
����d�����傫���Ȃ�ƁA�������g���̉������A�A�A�B�̏������݂����悤�ɂȂ�܂��B�����Ȃ�ƐF�������Ă��܂��B
����d������ɑ傫���Ȃ�ƁA���낢����g���̉������A�A�C�B�̏��������悤�ɂȂ�A���ɂ͐F�����Ȃ��Ȃ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B