���H�啨��'03�N�O��[2]
 �@�}�̂悤�ɁA
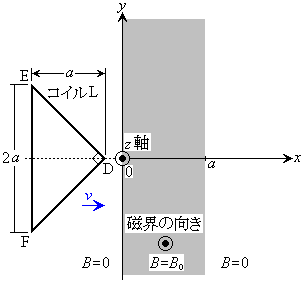
�@�}�̂悤�ɁA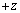 �����������Ă��鎥�E�̎������x�̑傫��B���Axy���ʂ�
�����������Ă��鎥�E�̎������x�̑傫��B���Axy���ʂ�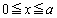 �ł�
�ł�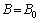 (�萔)�A����ȊO�ł�
(�萔)�A����ȊO�ł�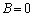 �ƂȂ��Ă����Ԃ�����B���̋�Ԃɒ�ӂ̒�����
�ƂȂ��Ă����Ԃ�����B���̋�Ԃɒ�ӂ̒�����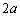 �C������a�ł���悤�Ȓ��p�ӎO�p�`DEF(���_D�����p)��1���R�C��L���A���̃R�C���ʂ�xy���ʂƈ�v����悤�ɒu���B�����Đ}�̂悤�ɐ���EF�̒��_���璸�_D�Ɍ�����������x���ƈ�v����悤�ɂ��āA
�C������a�ł���悤�Ȓ��p�ӎO�p�`DEF(���_D�����p)��1���R�C��L���A���̃R�C���ʂ�xy���ʂƈ�v����悤�ɒu���B�����Đ}�̂悤�ɐ���EF�̒��_���璸�_D�Ɍ�����������x���ƈ�v����悤�ɂ��āA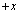 �����Ɉ��̑���v�ňړ�������B�Ȃ��A�R�C���̒�R��R�Ƃ��A�����̑����͖�������B�ݖ�(a)�`(d)�ł́A�R�C���̎��ȃC���_�N�^���X�͖���������̂Ƃ���B�܂��A����
�����Ɉ��̑���v�ňړ�������B�Ȃ��A�R�C���̒�R��R�Ƃ��A�����̑����͖�������B�ݖ�(a)�`(d)�ł́A�R�C���̎��ȃC���_�N�^���X�͖���������̂Ƃ���B�܂��A����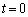 �ł͒��_D��
�ł͒��_D��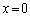 �ɂ���B
�ɂ���B
(a) ���L�̘g���ɓ��鎮����B
�R�C��L���т�����Φ�́A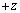 �����𐳂Ƃ���
�����𐳂Ƃ���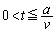 �ł�
�ł�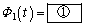 �ƂȂ�A
�ƂȂ�A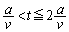 �ł�
�ł�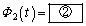 �ƂȂ�B
�ƂȂ�B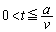 �ł́A����t�����������
�ł́A����t�����������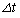 �����o�߂���
�����o�߂���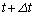 �ɂȂ����Ƃ��̎���
�ɂȂ����Ƃ��̎���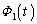 �̕ω���
�̕ω���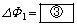 �ƂȂ�B���̂Ƃ�
�ƂȂ�B���̂Ƃ�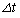 �̍��ɔ�r����
�̍��ɔ�r����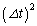 �̍����������Ƃ��Ė�������A�R�C���ɗU�N�����U���N�d��
�̍����������Ƃ��Ė�������A�R�C���ɗU�N�����U���N�d��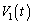 �́AD��E��F��D�ɉ����Ĕ�������N�d�͂𐳂Ƃ���
�́AD��E��F��D�ɉ����Ĕ�������N�d�͂𐳂Ƃ���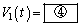 �ƕ\�����Ƃ��ł���B���l�ɂ��āA
�ƕ\�����Ƃ��ł���B���l�ɂ��āA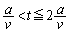 �ł̗U���N�d�͂�
�ł̗U���N�d�͂�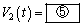 �ƂȂ�B
�ƂȂ�B (b) 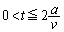 �ŃR�C��L�ɗ����d��I�̕ω������̃O���t�Ɏ����B���̖�ł̓d��I�̑傫���̍ő�l
�ŃR�C��L�ɗ����d��I�̕ω������̃O���t�Ɏ����B���̖�ł̓d��I�̑傫���̍ő�l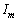 �����߂�B�������AD��E��F��D�ɉ����ė����d���̌����𐳂Ƃ���B
�����߂�B�������AD��E��F��D�ɉ����ė����d���̌����𐳂Ƃ���B (c) 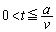 �ŃR�C��L���W���[���M�Ƃ��ď���Ă���d��P���A����t�̊��Ƃ��ĕ\���B
�ŃR�C��L���W���[���M�Ƃ��ď���Ă���d��P���A����t�̊��Ƃ��ĕ\���B (d) �R�C��L�����̑���v�ňړ������邽�߂ɊO��������Ă����F���A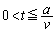 �Ŏ���t�̊��Ƃ��ċ��߂�B�������A
�Ŏ���t�̊��Ƃ��ċ��߂�B�������A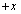 �����ɉ����Ă���͂𐳂Ƃ���B�܂�
�����ɉ����Ă���͂𐳂Ƃ���B�܂�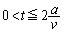 �ŃR�C��L�ɉ����Ă����F���A
�ŃR�C��L�ɉ����Ă����F���A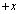 �����𐳂Ƃ��ĉ��̃O���t�ɂ����悻�̌`�������B
�����𐳂Ƃ��ĉ��̃O���t�ɂ����悻�̌`�������B (e) ���ɁA�R�C��L�̎��ȃC���_�N�^���X�������ł��Ȃ��ꍇ���l����B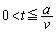 �̂Ƃ��̓d���̑傫���́A��������t�Ŕ�r�����ꍇ�A��L(b)�Œ��ׂ��d���̑傫�������傫���Ȃ邩�A�������Ȃ邩�A���邢�͕ς��Ȃ�������B�܂����̂悤�ɍl�������R��50���ȓ��ŋL���B
�̂Ƃ��̓d���̑傫���́A��������t�Ŕ�r�����ꍇ�A��L(b)�Œ��ׂ��d���̑傫�������傫���Ȃ邩�A�������Ȃ邩�A���邢�͕ς��Ȃ�������B�܂����̂悤�ɍl�������R��50���ȓ��ŋL���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���@���C�Ɋւ����{�I�ȏo��ł��B�t���~���O����̖@���A�d���U���̖@���A�����c�̖@�����Q�Ƃ��Ă��������B
���@���C�Ɋւ����{�I�ȏo��ł��B�t���~���O����̖@���A�d���U���̖@���A�����c�̖@�����Q�Ƃ��Ă��������B
���L�ł́A(a)�B�ŋߎ��O�̎�������Ă���̂ŁA�C��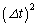 ������悤�ɉ��܂������A����́A�����I��
������悤�ɉ��܂������A����́A�����I��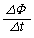 �ɂ����āA
�ɂ����āA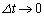 �Ƃ���������s���̂Ɠ�������ł����āA��������(
�Ƃ���������s���̂Ɠ�������ł����āA��������(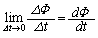 )�̂Ɠ����ł��B�D�ł́A�������ĉ��܂����B
)�̂Ɠ����ł��B�D�ł́A�������ĉ��܂����B
(a)�@ �R�C�������������ʉ߂��镔�����ʐ���S�Ƃ��܂��B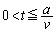 �ɂ�����R�C���̏�(t�b��)���E��}�Ɏ����܂��B
�ɂ�����R�C���̏�(t�b��)���E��}�Ɏ����܂��B ���̂Ƃ��A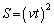
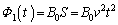 ......[��]
......[��] �A 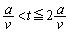 �ɂ�����R�C���̏�(t�b��)���E���}�Ɏ����܂��B
�ɂ�����R�C���̏�(t�b��)���E���}�Ɏ����܂��B ���̂Ƃ��R�C�������������ʉ߂��镔�����ʐ��́A
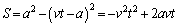
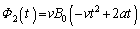 ......[��]
......[��]�B 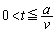 �ɂ����āA
�ɂ����āA 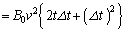 ......[��]
......[��]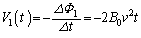 ......[��]�@(�����c�̖@���ɂ��A�N�d���̓R�C�����т����E����߂�����ŕ��ł�)
......[��]�@(�����c�̖@���ɂ��A�N�d���̓R�C�����т����E����߂�����ŕ��ł�)�D 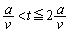 �ɂ����āA
�ɂ����āA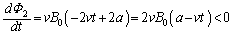
�����c�̖@�����A�N�d���͐�������A
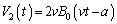 ......[��]
......[��]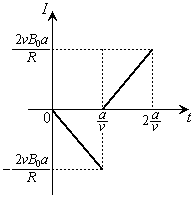
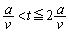 �ɂ����āA
�ɂ����āA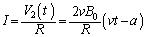 �d���̕ω��̃O���t�͉E�}�B
�d���̕ω��̃O���t�͉E�}�B
�O���t���A�d���̑傫���̍ő�l�F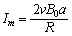 (
(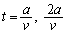 �̂Ƃ�) ......[��]
�̂Ƃ�) ......[��]
(c) 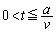 �ɂ����āA
�ɂ����āA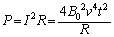 ......[��]
......[��]
(d) 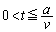 �ɂ����āA���E��DE��FD�ɋy�ڂ����́A�t���~���O����̖@���ɂ��x���������甽���v���ɁA���ꂼ��A
�ɂ����āA���E��DE��FD�ɋy�ڂ����́A�t���~���O����̖@���ɂ��x���������甽���v���ɁA���ꂼ��A �C
�C �̕����������܂��B����������x���������������A���̑傫��f��DE�ɓ�������
�̕����������܂��B����������x���������������A���̑傫��f��DE�ɓ�������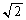 �{�ł��B�܂��A���E���ɑ��݂���DE�CFD�̕����������́A�e�X�A
�{�ł��B�܂��A���E���ɑ��݂���DE�CFD�̕����������́A�e�X�A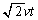 �ł��B�R�C���ɓ������̑傫��f�́A
�ł��B�R�C���ɓ������̑傫��f�́A �R�C���ɂ́A�R�C���������x�^�������邽�߂ɁA����Ƃ荇���O����������K�v������܂�(�͂̂荇�����Q��)�B
�R�C���ɉ������O����x���������������A 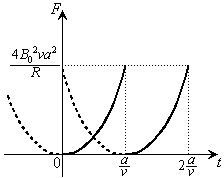
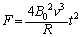 ......[��]
......[��]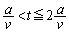 �ɂ����āADE��FD(���E���ɑ��݂��镔���������́A�e�X�A
�ɂ����āADE��FD(���E���ɑ��݂��镔���������́A�e�X�A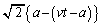 )�ɓ������̓t���~���O����̖@���ɂ��x���ɑ���
)�ɓ������̓t���~���O����̖@���ɂ��x���ɑ���
�����v����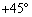 �C
�C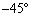 �̕����ŁA����������x���������������A�傫��
�̕����ŁA����������x���������������A�傫��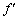 ��DE�ɓ�������
��DE�ɓ�������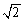 �{�ŁA
�{�ŁAEF�ɓ�������x���������������A�傫���́A
�O���́A
��F�̃O���t�͉E�}�B
(e) �d���̑傫���͏������Ȃ�B ......[��]
(���R) �����c�̖@���ɂ��A�R�C���ɂ͓d���̑����W��������̋N�d�͂�����邩��B ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B