���H�啨��'04�N�O��[1]
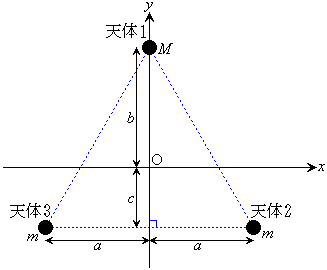 �@�}�̂悤��3�̓V�̂��݂��̖��L���͂��Ȃ��猴�_O�𒆐S�Ɉ��p���xω �œ���ʏ���~�^�����Ă���B�V��1�̎��ʂ�M�C�V��2�C3�̎��ʂ�m�Ƃ���B���̑��ɓV�̂͂Ȃ����̂Ƃ���B�ȉ��A�V�̂ƈꏏ�ɉ�]���Ă���ϑ��҂̗��ꂩ��l�@���A�}���̓�̒������鎲x�Cy�͓����p���xω �ʼn�]���Ă�����̂Ƃ���B���̂悤��3�̓V�̂����p���x�ʼn^������ɂ͐}�̋���a�Cb�Cc�Ԃɂ���W������������Ă��Ȃ���Ȃ�Ȃ��B���L���͒萔��G�Ƃ���B�ȉ��̐ݖ�ɓ�����B���ɓV��1�ƓV��2�̋���
�@�}�̂悤��3�̓V�̂��݂��̖��L���͂��Ȃ��猴�_O�𒆐S�Ɉ��p���xω �œ���ʏ���~�^�����Ă���B�V��1�̎��ʂ�M�C�V��2�C3�̎��ʂ�m�Ƃ���B���̑��ɓV�̂͂Ȃ����̂Ƃ���B�ȉ��A�V�̂ƈꏏ�ɉ�]���Ă���ϑ��҂̗��ꂩ��l�@���A�}���̓�̒������鎲x�Cy�͓����p���xω �ʼn�]���Ă�����̂Ƃ���B���̂悤��3�̓V�̂����p���x�ʼn^������ɂ͐}�̋���a�Cb�Cc�Ԃɂ���W������������Ă��Ȃ���Ȃ�Ȃ��B���L���͒萔��G�Ƃ���B�ȉ��̐ݖ�ɓ�����B���ɓV��1�ƓV��2�̋���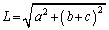 ��p���Ă悢�B
��p���Ă悢�B
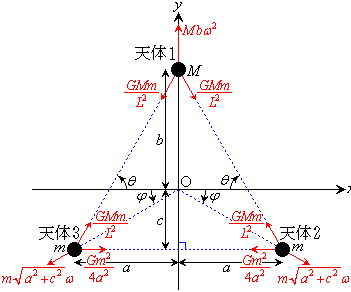
(a) �e�X�̓V�̊Ԃɓ������L���͂ƁA���ꂼ��̓V�̂̉��S�͂̌�����}���Ɏ����A�����̑傫�����L������B
(b) �e�X�̓V�̂ł̗͂̂荇���̎���x��������y�������ɕ������ď����B
(c) ��]�̒��SO��3�̓V�̂̏d�S�ɂȂ��Ă��邱�Ƃ������B
(d) 3�̓V�̂̈ʒu�����O�p�`�̒��_�ɂ��邱�Ƃ������B
(e) �p���xω ��G�CM�Cm�Ca��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ς����Ȗ��Ɍ����܂����A�w���ɏ]���ė������Ă��܂��A���Ƃ́A�Ђ�����A�v�Z���邾���̖��ł��B
(a) �E�}�ɂ����āA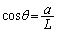 �C
�C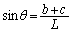 �C
�C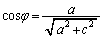 �C
�C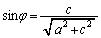 ����@
����@ �V��1�ƓV��2�C�V��1�ƓV��3�Ƃ�������L������A���҂̊Ԃɓ������L������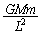
�V��2�ƓV��3�Ƃ�������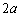 ������A���҂̊Ԃɓ������L������
������A���҂̊Ԃɓ������L������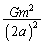
�V��1�������S����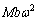
�V��2�C�V��3�������S����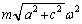
�����̗͂�}�ɏ������ނƉE�}�B
(b) �V��1�ɂ��āAx�����F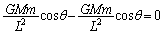
�@���A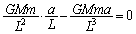 y�����F
y�����F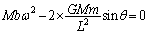
�@���A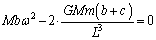 ����@
����@
�V��2�ƓV��3�ɂ��āAx�����F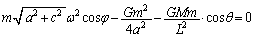
�@���A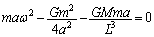 ����Ay�����F
����Ay�����F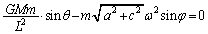
�@���A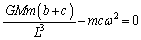 ����B
����B
(c) 3�̓V�̂̏d�S��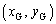 �Ƃ��āA
�Ƃ��āA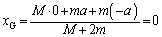 �C
�C ����C
����C �C����b�Cc���܂ނ̂ŁA�@�C�B�𗘗p���܂��B
�B���A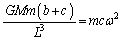
������@�ɑ������ƁA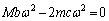
�� 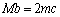 ����D
����D
������C�ɑ������ƁA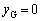
����āA3�̓V�̂̏d�S��O�ł��B
(d) 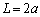 ��������悢�킯�ł��B�܂��A
��������悢�킯�ł��B�܂��A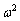 ���������܂��B
���������܂��B �B���A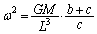
�D���A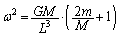 ����E
����E
������A�ɑ������ƁA ��������ƁA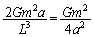
�� 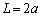 ����āA2�̓V�̂͐��O�p�`�̒��_�ɂ���܂��B
����āA2�̓V�̂͐��O�p�`�̒��_�ɂ���܂��B
(e) 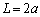 ���E�ɑ������ƁA
���E�ɑ������ƁA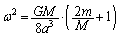
�� 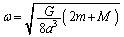 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B